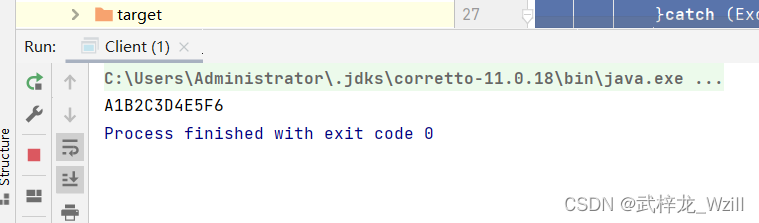
方格取数

走两次的最大值

 f[k][i1][i2]来表示

k = i1 + j1 = i2 + j2;

每一个状态可由四种状态转换来，分别为

第一条路走下，第二条路走下

第一条路走下，第二条路走右

第一条路走右，第二条路走下

第一条路走右，第二条路走右

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
 
using namespace std;
 
typedef pair<int, int> PII;
typedef long long ll;
typedef pair<ll, int> PLI;

const int N = 15;

int n;
int a[N][N];
int f[N + N][N][N];

int main()
{
	IOS
	int n;
	cin >> n;
	int x, y, c;
	while(cin >> x >> y >> c, x)
	{
		a[x][y] = c;
	}
	
	for(int k = 2; k <= n + n; k ++)
	{
		int t1 = min(n, k - 1);//j的范围是1~n j=n时i最小，j=1时i最大
		for(int i1 = max(1, k - n); i1 <= t1; i1 ++)
		{
			for(int i2 = max(1, k - n); i2 <= t1; i2 ++)
			{
				int j1 = k - i1, j2 = k - i2;
				int t = a[i1][j1];
				if(i1 != i2)t += a[i2][j2];
				
				f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][i1 - 1][i2 - 1] + t);
				f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][i1 - 1][i2] + t);
				f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][i1][i2 - 1] + t);
				f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][i1][i2] + t);
			}
		}
	}
	cout << f[n + n][n][n];
	
	return 0;
}