41题

(1) 最坏情况下比较的总次数
对于长度分别为 m,n 的两个有序表的合并过程,最坏情况下需要一直比较到两个表的表尾元素,比较次数为 m+n-1 次。已知需要 5 次两两合并,故设总比较次数为 X-5, X 就是以 N 个叶子结点表示升序表,以升序表的表长表示结点权重,构造的二叉树的带权路径长度。故只需设计方案使得 X 最小。设计哈夫曼树如下:
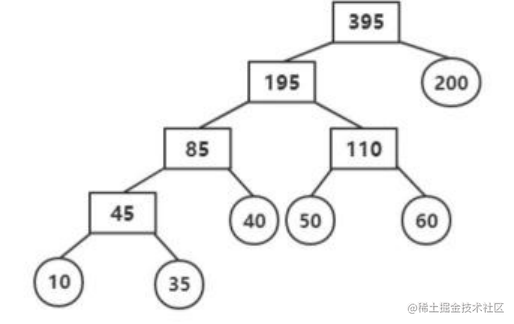
这样, 最坏情况下比较的总次数为:
N=(10+35)x4+(40+50+60)x3+200-5=825
(2) N (N≥2)个不等长升序表的合并策略:
以 N 个叶子结点表示升序表, 以升序表的表长表示结点权重, 构造哈夫曼树合并时,从深度最大的结点所代表的升序表开始合并,依深度次序一直进行到根结点。
理由: N 个有序表合并需要进行 N- 1 次两两合并,可设最坏情况下的比较总次数为 X-N+1,X 就是以 N 个叶子结点表示升序表, 以升序表的表长 表示结点权重,构造的二叉树的带权路径长度。根据哈夫曼树的特点,上述设计的比较次数是最小的。
42题
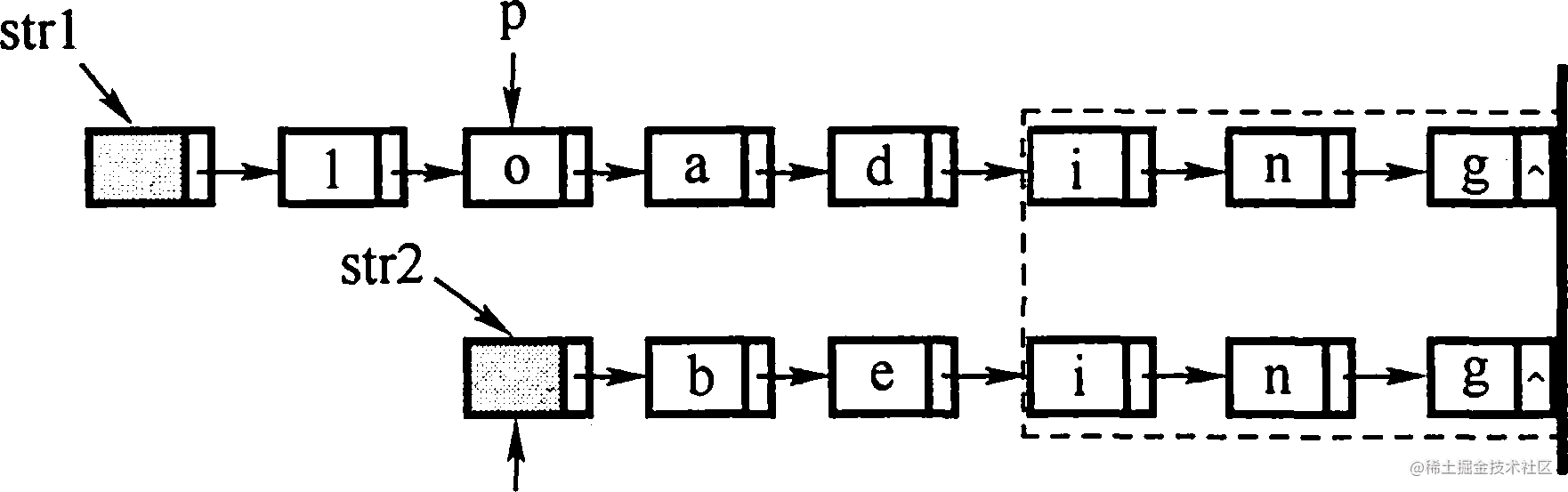
假定采用带头结点的单链表保存单词,当两个单词有相同的后缀,则可共享相同的后缀存储空间, 例如,“loaging"和"being”, 如下图所示。
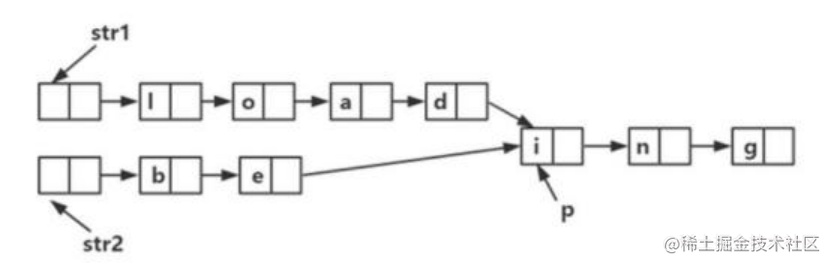
设 str1 和 str2 分别指向两个单词所在单链表的头结点, 链表结点结构为

请设计一个时间上尽可能高效的算法,找出由 str1 和 str2 所指向两个链表
共同后缀的起始位置(如图中字符 i 所在结点的位置 p)。
要求:
最优解:
(1) 给出算法的基本设计思想。
顺序遍历两个链表到尾结点时,并不能保证两个链表同时到达尾结点。这是 因为两个链表的长度不同。假设一个链表比另一个链表长 k 个结点, 我们 先在长链表上遍历 k 个结点, 之后同步遍历两个链表。这样我们就能够保 证它们同时到达最后一个结点了。由于两个链表从第一个公共结点到链表 的尾结点都是重合的。所以它们肯定同时到达第一个公共结点。
算法的基本设计思想:
- 分别求出 str1 和 str2 所指的两个链表的长度 m 和 n。
- 将两个链表以表尾对齐: 令指针 p、q 分别指 str1 和 str2 的头结点,若 m>=n,则使p指向链表中的第 m-n+1个结点; 若m<n,则使q 指向链表中的第 n-m+1 个结点,即使指针 p 和 q 所指的结点到表尾的长度相等。
- 反复将指针 p 和 q 同向后移动,并判断它们是否指同一结点。若 p 和 q 指向同一结点,则该点即为所求的共同后缀的起始位置。
简单来说就是:
① 求它们的长度 len1, len2;
② 遍历两个链表, 使 p, q 指向的链表等长;
④ 同步遍历两个链表, 直至找到相同结点或链表结束。
(2) 根据设计思想, 采用 C 或 C++或 java 语言描述算法,关键之处给出注释。
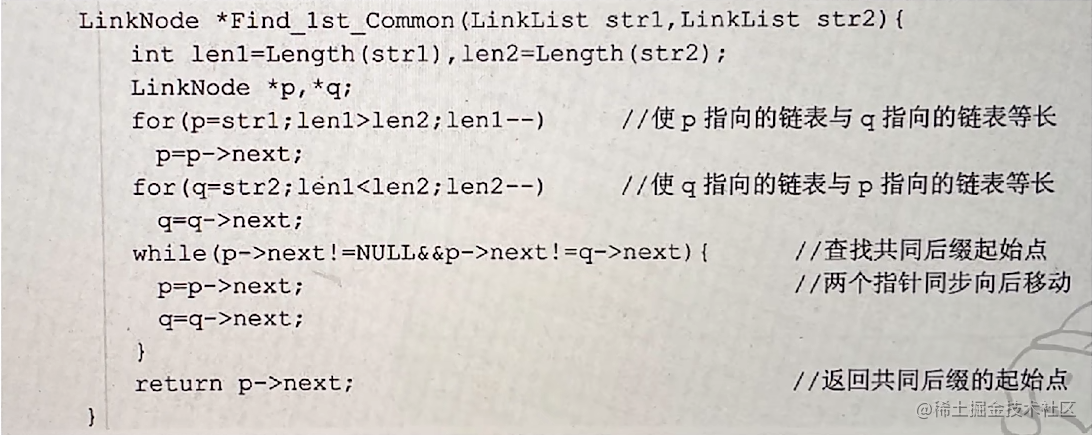
(3) 说明你所设计算法的时空复杂度。
时间复杂度为O(len1+len2)或O(max(len1,len2)), 其中len1、 len2分别为两个链表 的
长度。
暴力解:
定义两个指针P和G,分别指向想象中的链表,每遍历一个字符i,就全部遍历一次g所指向的单词,所有比较一次。
- P不为空一直往前走
- g不空往前走
- 两者判断比较
#include <cstddef>
typedef struct Lnode { //链表结点的结构定义
int data;
struct Lnode* next;
} Lnode,* Linklist;
Linklist searchCommon(Linklist L1, Linklist L2) {
LinkTist p = L1->next;
Linklist g = L2->next;
while (p != NULL) {
while (g != NULL) {
if (p == g) {
return g;
}
g = g->next;
}
p = p->next;
g = g->next;
return NULL;
}
}