个人主页：兜里有颗棉花糖
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创
收录于专栏【AcWing算法提高学习专栏】【手撕算法系列专栏】
🍔本专栏旨在提高自己算法能力的同时，记录一下自己的学习过程，希望对大家有所帮助
🍓希望我们一起努力、成长，共同进步。

原题链接：点击直接跳转到该题目

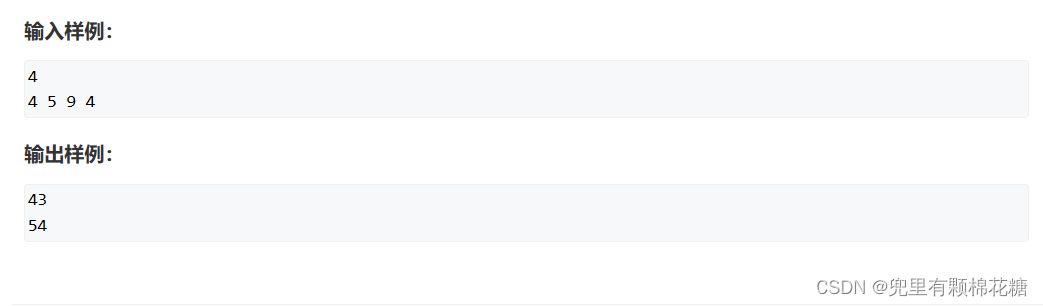
1️⃣题目描述

2️⃣题目解析

本题跟普通的链式石子合并不同的点就是由链式改为了环式数组了，那我们可以想一个方法将这个环式数组变为链式数组。

由于本题是一个链式数组，所以最终的答案不一定是[1,n]区间，也可能是[2,n + 1]，[3,n + 2]…[n,n + (n - 1)]。

例如：环形（a,b,c,d）最终的结果区间可能是[a,b,c,d]、[b,c,d,a]、[c,d,a,b]、[d,a,b,c]4种区间中的任意一种。

所以我们本题的解题策略是将环形数组转换为链式数组（即将其复制一遍连接在原数组的后面）。即(a,b,c,d,a,b,c,d)。这样的话我们就可以使用链式数组的解决方法来解决本题了。

3️⃣解题代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 410,INF = 0x3f3f3f3f;
int f[N][N],g[N][N];
int arr[N],s[N];

int main()
{
    int n;
    cin >> n;
    for(int i = 1;i <= n;i++)
    {
        cin >> arr[i];
        arr[i + n] = arr[i];
    }
    for(int i = 1;i <= 2 * n;i++) s[i] = s[i - 1] + arr[i]; // 创建前缀和数组
    
    memset(f,0x3f,sizeof f);
    memset(g,-0x3f,sizeof g);
    
    for(int len = 1;len <= n;len++)
    {
        for(int i = 1;i + len -1 <= n * 2;i++) // 区间左端点
        {
            int j = i + len - 1;
            if(len == 1) f[i][j] = g[i][j] = 0;
            else
            {
                 for(int k = i;k < j;k++)
                {
                    f[i][j] = min(f[i][j],f[i][k] + f[k + 1][j] + s[j] - s[i - 1]);
                    g[i][j] = max(g[i][j],g[i][k] + g[k + 1][j] + s[j] - s[i - 1]);
                }
            }
           
        }
    }
    
    int max_Res = -INF,min_Res = INF;
    for(int i = 1;i <= n;i++)
    {
        min_Res = min(min_Res,f[i][i + n - 1]);
        max_Res = max(max_Res,g[i][i + n - 1]);
    }
    cout << min_Res << endl << max_Res << endl;
    return 0;
}

最后代码就顺利通过啦！！！