系列文章目录

---

---

前言

从线性查找入手算法。

---

一、线性查找

线性查找
目的	在线性数据结构中一个一个查找目标元素
输入	数组和目标元素
输出	目标元素所在的索引；若不存在，返回-1

二、实现查找算法

public class LinearSearch {

    private LinearSearch(){}
    //构造函数私有化

    public static <E> int search(E[] data, E target)
    {
        for(int i = 0;i < data.length;i++)
        {
            if(data[i].equals(target))
                return i;

        }
        return -1;
    }
}

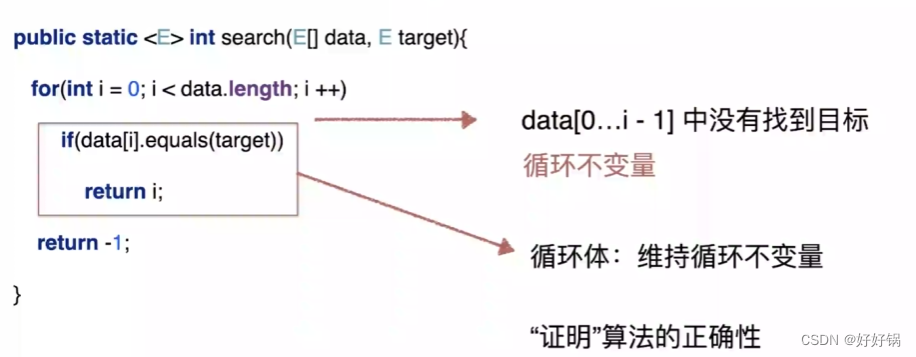
三、循环不变量

循环的目的
维持循环不变量

四、复杂度分析

算法复杂度分析	T = o(?)
分析	通过计算执行指令量（数据的规模）来衡量算法的复杂度，最终让算法的复杂度归结某一个量级，再来进行比较算法的性能
复杂度	随着数据规模n的增大，算法性能的变化趋势

五、常见复杂度

复杂度估算量级
时间复杂度的计算与数据规模相关，要先确定数据规模

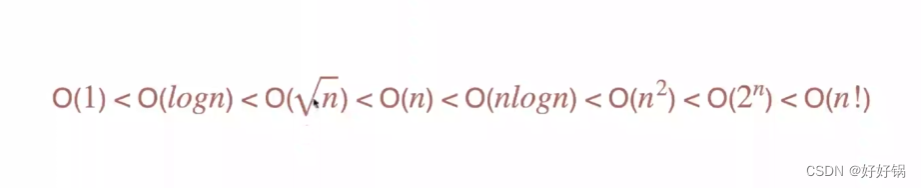
六、测试算法性能

public class ArrayGenerator {

    public static Integer[] generateOrderedArray(int n)
    {
        Integer[] arr = new Integer[n];
        for(int i = 0;i < n;i++)
        {
            arr[i] = i;
        }

        return arr;
    }
}

public class Main {
    public static void main(String[] args)
    {
        int[] dataSize = {100000, 1000000};


        for(int n:dataSize)
        {
            Integer[] data = ArrayGenerator.generateOrderedArray(n);
            long startTime = System.nanoTime();
            for(int k = 0;k < 100;k++)
                LinearSearch.search(data, n);
            long endTime = System.nanoTime();
            double time = (endTime - startTime) / 1000000000.0;

            System.out.println("n = " + n + ",100 runs," + time + "s");
        }



    }
}

---

总结

算法复杂度需要结合数据规模进行分析，要看懂一个算法需要找到循环不变量和数据规模。