题目
城市C是一个非常繁忙的大都市,城市中的道路十分的拥挤,于是市长决定对其中的道路进行改造。
城市C的道路是这样分布的:
城市中有 n 个交叉路口,编号是 1∼n ,有些交叉路口之间有道路相连,两个交叉路口之间最多有一条道路相连接。
这些道路是 双向 的,且把所有的交叉路口直接或间接的连接起来了。
每条道路都有一个分值,分值越小表示这个道路越繁忙,越需要进行改造。
但是市政府的资金有限,市长希望进行改造的道路越少越好,于是他提出下面的要求:
1.改造的那些道路能够把所有的交叉路口直接或间接的连通起来。
2.在满足要求1的情况下,改造的道路尽量少。
3.在满足要求1、2的情况下,改造的那些道路中分值最大值尽量小。
作为市规划局的你,应当作出最佳的决策,选择哪些道路应当被修建。
输入格式
第一行有两个整数 n,m 表示城市有 n 个交叉路口,m 条道路。
接下来 m 行是对每条道路的描述,每行包含三个整数u,v,c 表示交叉路口 u 和 v 之间有道路相连,分值为 c。
输出格式
两个整数 s,max,表示你选出了几条道路,分值最大的那条道路的分值是多少。
数据范围
1 ≤ n ≤ 300,
1 ≤ m ≤ 8000,
1 ≤ c ≤ 10000
思路
样例:
4 5
1 2 3
1 4 5
2 4 7
2 3 6
3 4 8根据以上样例,我们可以得到一张图 :
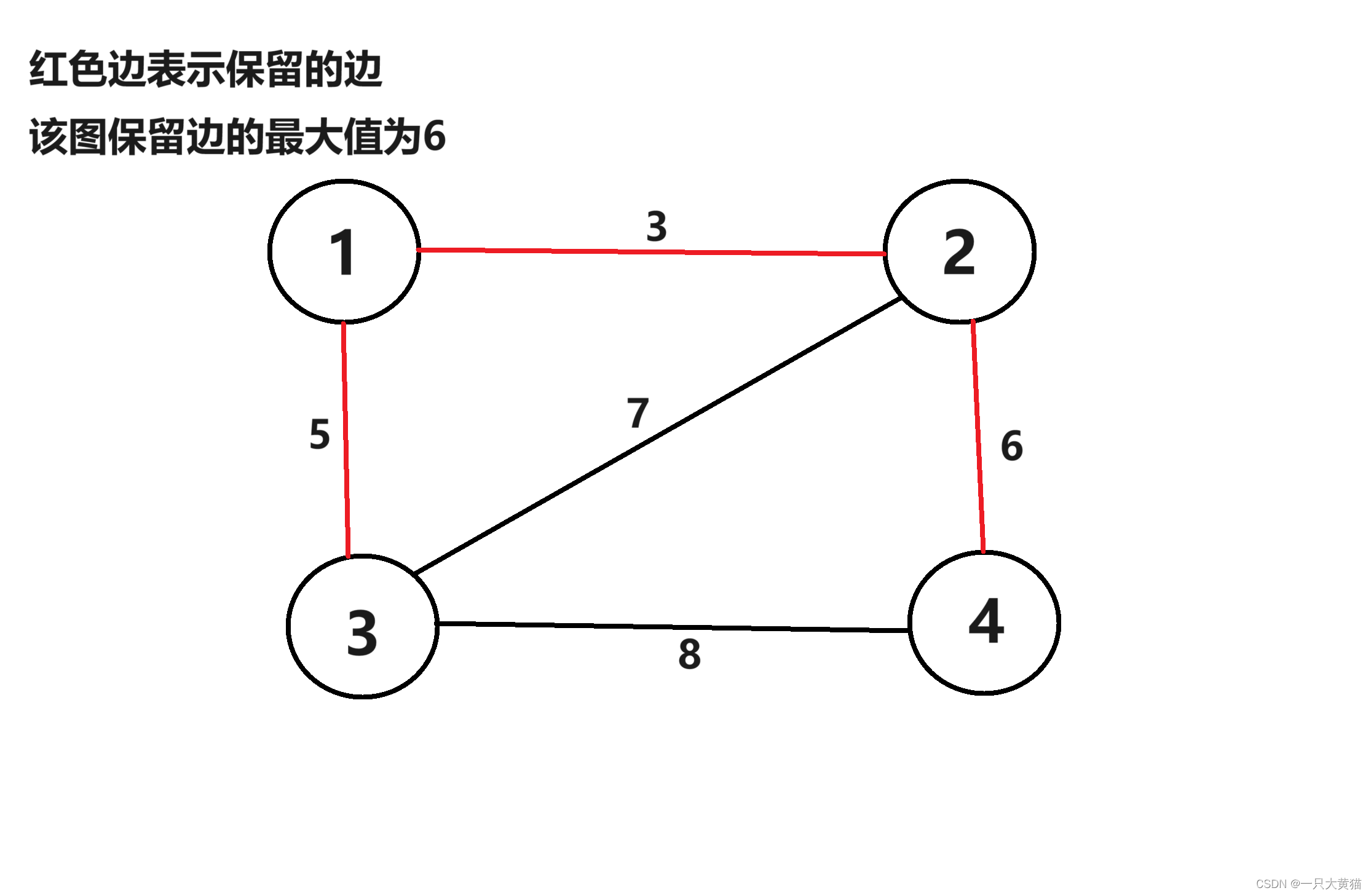
运用并查集的思路(集合两两合并,初始状态没个点分别为一个集合),如果想要得到一颗最小生成树需要合并n - 1次。
将边按照从小到大的顺序排序,从最小的的边开始遍历,如果当前边的两个点不在一个集合中,则合并这两个点所在的集合,如果边权大于之前合并的两点之间的边的边权,则保留。如果这两个点在一个集合中则什么也不做。
当合并次数到达n - 1次时,最小生成树构造完成。输出 n - 1(合并次数,最小生成树的边数)与最小生成树的最大边权。
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 310,M = 8010;
int n,m;
int p[M];
struct edges{
int a,b,c;
}edge[M];
bool cmp(edges x, edges y)
{
return x.c < y.c;
}
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> m;
for(int i = 0; i <= n; i ++) p[i] = i;
for(int i = 0; i < m; i ++)
{
int a,b,c;
cin >> a >> b >> c;
edge[i] = {a,b,c};
}
sort(edge,edge + m,cmp);
int ans = 0;
int flag = 0;
for(int i = 0; i < m; i ++)
{
int a = find(edge[i].a);
int b = find(edge[i].b);
if(p[a] != p[b])
{
flag ++;
p[a] = b;
ans = max(ans,edge[i].c);
}
if(flag == n - 1) break;
}
cout << -- n << " " << ans << endl;
return 0;
}题目来自: https://www.acwing.com/