公开数据集中文版详细描述参考前文:https://editor.csdn.net/md/?not_checkout=1&spm=1011.2124.3001.6192
目录
- 0. 公开数据集
- 1. 神经元的raster和PSTH图
- 1.1 Raster
- 1.2 PSTH
- 2. 运动轨迹图 (center_out)
- 3. 神经元的运动调制曲线 (tuning curve)
0. 公开数据集
- 网址:Nonhuman Primate Reaching with Multichannel Sensorimotor Cortex Electrophysiology 1
- Session:" indy_20170124_01 "
1. 神经元的raster和PSTH图
1.1 Raster
神经元的raster图是一种用于可视化神经元活动的图表,它以时间为横轴,每个神经元的不同脉冲或活动事件为纵轴。每个脉冲或事件用一个点或线表示,多个神经元的活动可以在同一个图表中显示,以便比较它们的活动模式。
在这里,我们将猕猴控制光标向一个新出现的target移动的全过程作为一个trial,并且将二维界面划分为8个不同的方向作为不同的condition,神经元的raster图呈现选定神经元在某一个condition下的所有trials的spike活动。具体处理如下:
- 提取Spike矩阵:我们将神经元全时程的发放率阈值设定为2,然后从原始数据中得到spike矩阵为[n_neuron, n_time]。其中n_neuron代表预处理后的神经元个数,n_time为整个session的所有时间点,这里“spike_array = [138, 147501]”。
- 划分trials:每一个新的target对应一个trial,由于第一个trial没有规定好的初始位置,所以我们只考虑后486个;同时将360度的二维界面等分为8个方向,即8种不同的conditions。
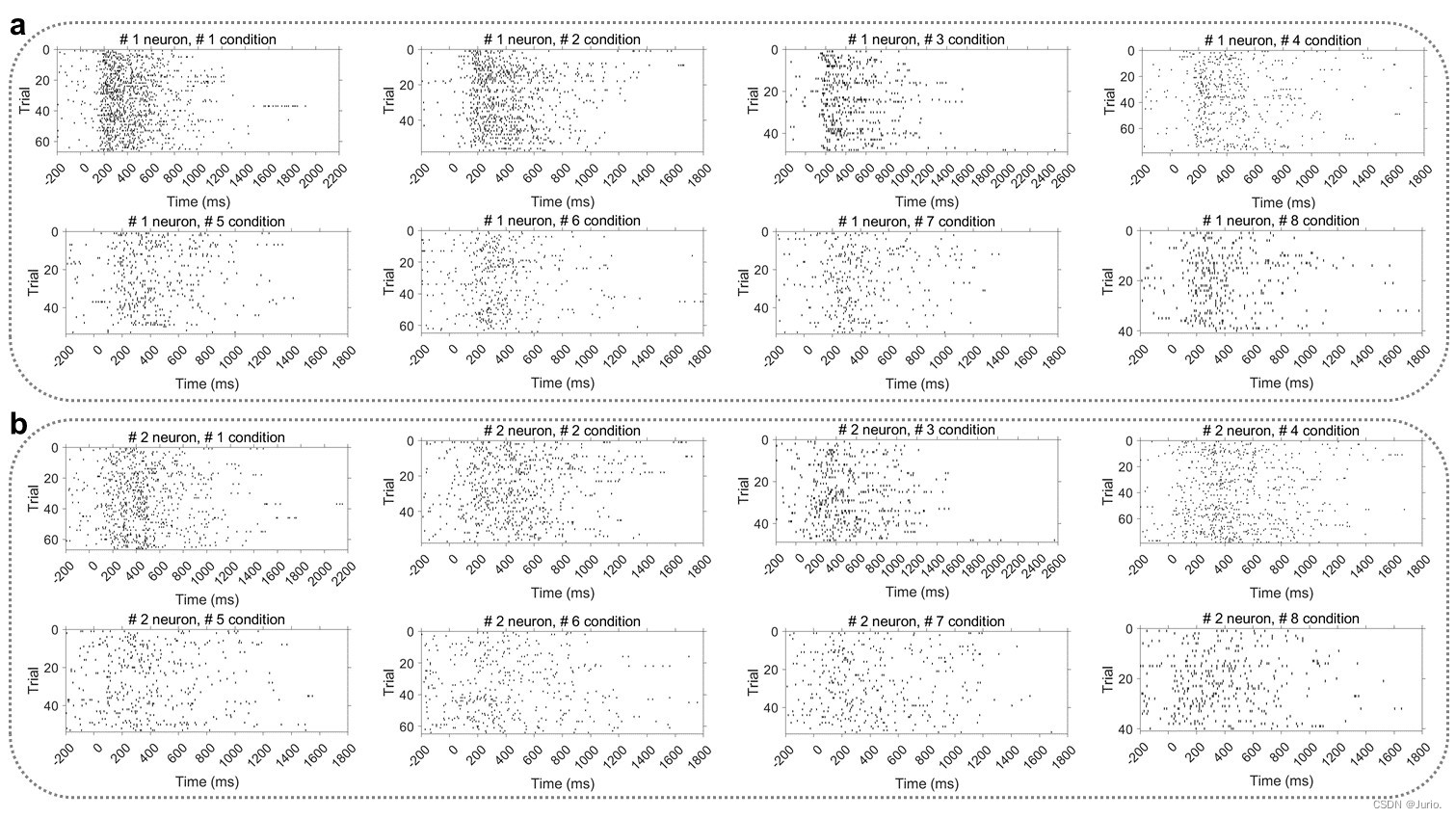
- 绘制raster:我们选定138个神经元中的前两个,以new_target出现为原点,最长的trial时长为时间轴右边界,-200 ms的上文信息为左边界;将8个方向作为不同conditions,纵轴为当前condition的所有trials。
神经元1-2的raster图如 Figure 1 所示:
1.2 PSTH
PSTH(Peri-Stimulus Time Histogram)图是一种用于显示神经元对特定刺激或事件的响应模式的图表。它以时间为横轴,神经元的活动频率为纵轴,显示在特定时间段内神经元的活动频率。PSTH图通常用于研究神经元对刺激的响应时间和模式。
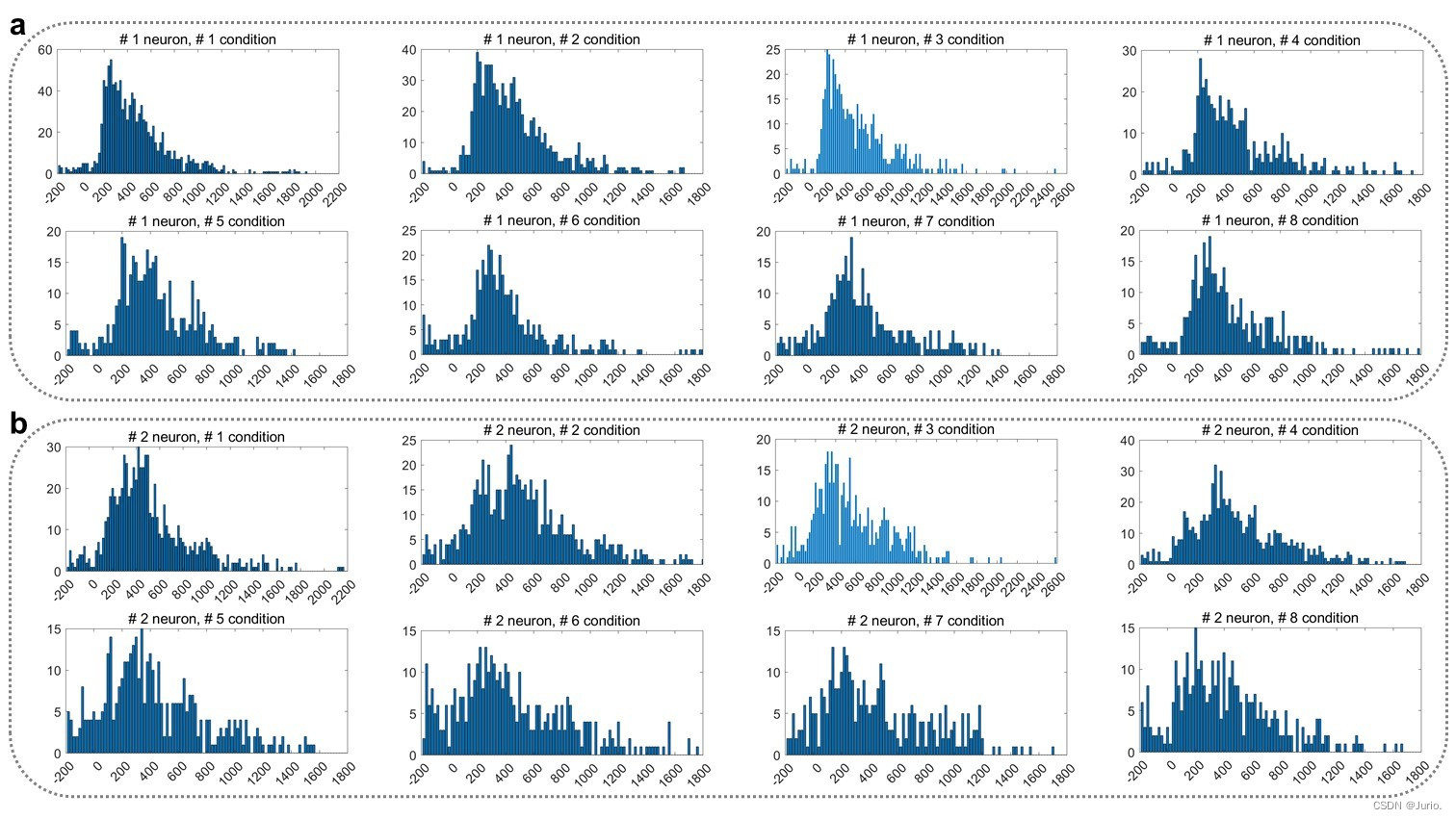
在这里,我们沿用上一节的数据预处理方式,然后将一个时间段bin大小设为20ms,由于神经信号采样率为250Hz,即一个bin包含5个数据点。我们神经元在单个bin内的所有发放trials个数作为其活动频率的指标,其他设置同raster,最终得到前两个神经元的PSTH图如 Figure 2 所示:
2. 运动轨迹图 (center_out)
神经元的运动轨迹图(center_out)是一种常用的方法来可视化神经元的活动模式。该图可以用来显示神经元在不同中心位置的刺激下的活跃程度。通常,"center_out"图使用极坐标来表示刺激的方向和距离。刺激的中心位置通常位于圆心,而刺激的方向和距离则通过圆周上的点来表示。
在这里,我们绘制了前30个trials的8个不同方向的光标运动轨迹作为center_out图,不同的方向用不同的颜色表示,如 Figure 3 所示:

3. 神经元的运动调制曲线 (tuning curve)
神经元的调谐曲线(tuning curve)是一种常用的方法来描述神经元对于不同刺激参数(例如方向、频率、强度等)的响应模式。调谐曲线可以展示神经元在不同刺激参数取值下的活动水平。
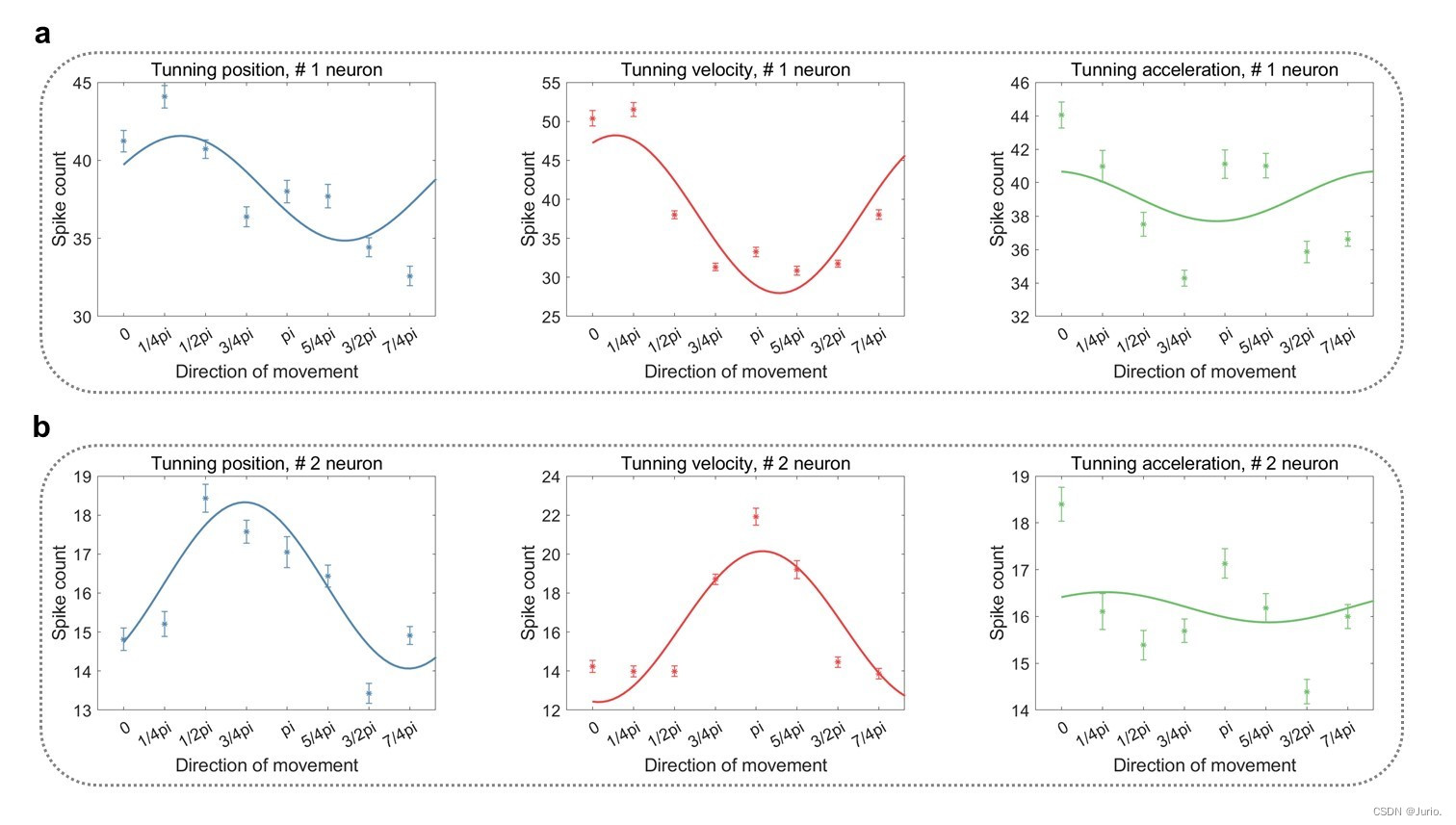
一般来说,神经元对角度的tuning倾向正弦曲线的形式,所以我们这里采用正弦函数来建模神经元的响应模式。同样地,我们对前两个神经元分别绘制了在位置、速度和加速度上的调谐曲线:
Makin, J. G., O’Doherty, J. E., Cardoso, M. M. B. & Sabes, P. N. (2018). Superior arm-movement decoding from cortex with a new, unsupervised-learning algorithm. J Neural Eng. 15(2): 026010. doi:10.1088/1741-2552/aa9e95 ↩︎