题目描述

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

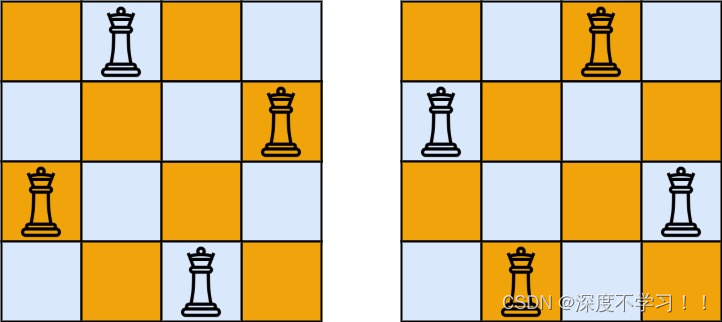
输入：n = 4
输出：[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

思路分析

【这道题不难，相信我】
【这道题不难，相信我】
【这道题不难，相信我】
【这道题不难，相信我】
【这道题不难，相信我】
【这道题不难，相信我】
【这道题不难，相信我】
【这道题不难，相信我】

我知道很多兄弟看到这个题就直接不读题劝退了，实际上这道题没那么难，我觉得甚至没有那道中等难度的电话号码组合回溯题难。

首先，解释一下题目。压根不用管什么国际象棋。

就是给一个二维数组， n*n的。里面可以放一个棋子(题目叫皇后)，这个棋子必须满足三个特性：行， 列， 对角线 均只有一个，跟数独一样。

直接回溯，开始画树。

偷了张图，方便理解：

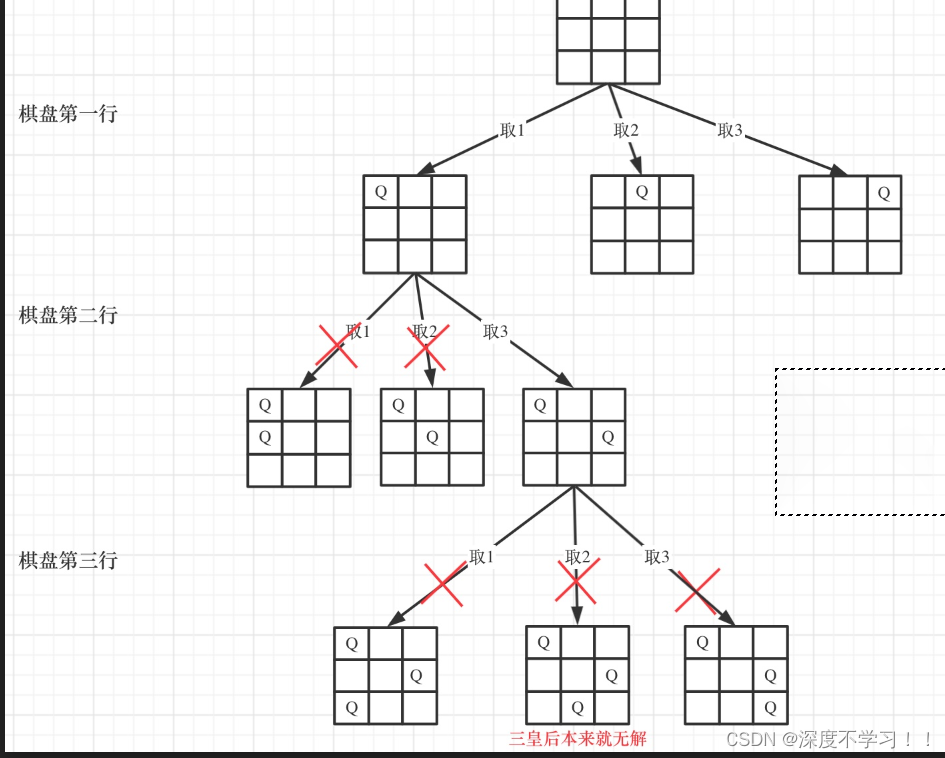
上面这棵树可以理解成，每一层就是遍历二维数组的每一行，然后暴力穷举放置皇后Q这个棋子，看看是否合法。

那么这道题就转换成要解决两个问题：

• 问题1：穷举所有皇后棋子Q的放置情况
• 问题2：判断放置棋子后是否合法

对于问题1

这个很好解决啊，做过回溯的应该都能秒解。

我们设置当前遍历的行为row。
题目给的值为n，表示n*n的二维数组。

回溯终止条件：

当前遍历的row是最后一行的时候，也就是row==n的时候，终止。
将当前Q的放置方案加入答案集。
注意，这里并不需要判断放置方案是否合法，因为合法性在前面已经判断过了，不合法的不会走到这一步。

			if row == n:
                tmp = [''.join(i) for i in board]
                res.append(tmp)
                return

遍历回溯体：

这里没得说，先判断合法性，不合法直接循环下一轮，合法的话，当前位置放皇后，然后继续往下一层遍历。

      		for col in range(n):
                # 如果当前放皇后Q不合法：
                    continue
                board[row][col] = 'Q'
                backtrack(row + 1)
                board[row][col] = '.'

对于问题2

这个也不难。就是判断当前防止皇后Q的位置是否合法。
当前层的Q是否合法，其实就是判断他的行，列，对角线是否有Q。因为下面的还没遍历嘛，肯定没有Q，所以不用判断。

行：不用判断，这一点直接看上面那个图就知道了，每一行都是放了一个，合法就往下走不合法就遍历一下个位置了。

列：实际上是判断当前位置的正上方有没有Q。

		# 查看正上方是否有Q
        for i in range(row):
            if board[i][col] == 'Q':
                return False

对角线：分为正负对角线。其实就是 当前位置的左上方对角线和右上方对角线有没有Q

		# 查看右上方是否有Q
        for i, j in zip(range(row - 1, -1, -1), range(col + 1, n, 1)):
            if board[i][j] == 'Q':
                return False

        # 查看左上方是否有Q
        for i, j in zip(range(row - 1, -1, -1), range(col - 1, -1, -1)):
            if board[i][j] == 'Q':
                return False

完整代码

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        # 从上往下放棋子
        # row表示当前遍历的是第几行，也就是树的第几层
        board = [['.'] * n for _ in range(n)]
        res = []
        def backtrack(row):
            n = len(board)
            # 如果到最后一行了，则将结果添加到res里
            if row == n:
                tmp = [''.join(i) for i in board]
                res.append(tmp)
                return

            for col in range(n):
                if not self.isValid(board, row, col):
                    continue
                board[row][col] = 'Q'
                backtrack(row + 1)
                board[row][col] = '.'
        backtrack(0)

        return res



    def isValid(self, board, row, col):
        n = len(board)

        # 查看上方是否有Q
        for i in range(row):
            if board[i][col] == 'Q':
                return False

        # 查看右上方是否有Q
        for i, j in zip(range(row - 1, -1, -1), range(col + 1, n, 1)):
            if board[i][j] == 'Q':
                return False

        # 查看左上方是否有Q
        for i, j in zip(range(row - 1, -1, -1), range(col - 1, -1, -1)):
            if board[i][j] == 'Q':
                return False

        return True