要学习红黑树节点的插入那么首先就要了解什么是红黑树,以及红黑树的特点。
红黑树的特点
本来AVL树已经很厉害了,但是红黑树的总体效率略比1AVL树高。高的大体原因。我们先来看一下红黑树和AVL树的区别。

AVL树严格的保证了左子树和右子树的高度差不超过1,而红黑树则是保证了最长路径不超过最短路径的2倍。这里可以理解成AVL树是极其相似于一棵完全二叉树了,而红黑树则不是。
所以如果这里存在100w个节点,那么AVL树则再20层左右,而红黑树则在20到40层左右
这里虽然看起来红黑树和AVL树之间相差了那么多层,但是对于cpu而言,这两者的时间是差不多的。
而AVL树要完成这个严格的平衡付出了更多代价(更多的旋转)
而红黑树虽然也存在旋转但是相对而言少了很多的旋转。这也正是红黑树,效率略高的原因.
红黑树的性质
下面我们来看红黑树的性质。

注意的是这里的第5点的叶子节点是指的空节点,而不是我们之前认为的那个叶子节点,引入5号规则是为了便于我们数清楚路径
下面解析三号规则:

然后是4号规则:

根据3号和4号规则就能够解决上面的那个思考题目。
原因如下我们首先思考最短和最长路径的构成。
由此就能够得到下面的结论

其中最短路径是更具第三条和第四条规则得出的,而最长路径则是再最短路径的基础上根据3号规则得出。当我们知道了最短路径之后,对于最长路径,我们肯定不能再增加黑色节点否则不符合规则,那么就只能是增加红色节点,而红色节点不能连续,由此得出的最长路径。
从规则中我们还可以知道如果这个节点全是黑色的也是存在的。例如下面这样
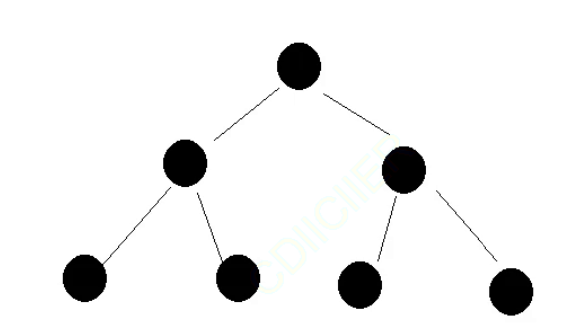
这里解释一下5号规则,那些所谓的叶子节点其实是NIL节点。
而这些节点的功能是帮助我们数清楚改红黑树存在多少条路经的,
例如上面的那个图就存在8条路径。这里记住

上图中的那些红色的圆圈就是NIF节点共有7个,7条路经。
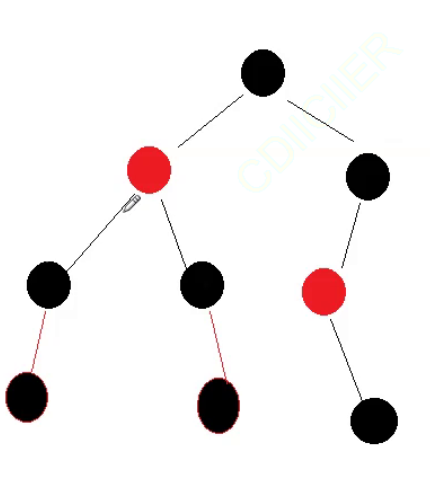
这一个图就是一个非红黑树的图,但是如果你数路径不是到达空的位置的话,那么你就会认为这里是一个红黑树。
分析插入的情况
下面我们来解决模拟实现的一些小细节:
第一点就是:现在需要往一棵红黑树中插入一个新节点,那么这个新节点的初始颜色应该是什么呢?
首先如果我们需要插入的这颗红黑树如果是一个空树,那么这个时候插入的第一个节点一定是黑色的。
那么现在下面存在一棵红黑树

下面需要增加一个节点,那么这个节点的颜色应该是什么呢?
此时如果插入的是黑色的节点,会导致每一条路径都受到影响,因为每一条路径都存在相同的黑色节点。
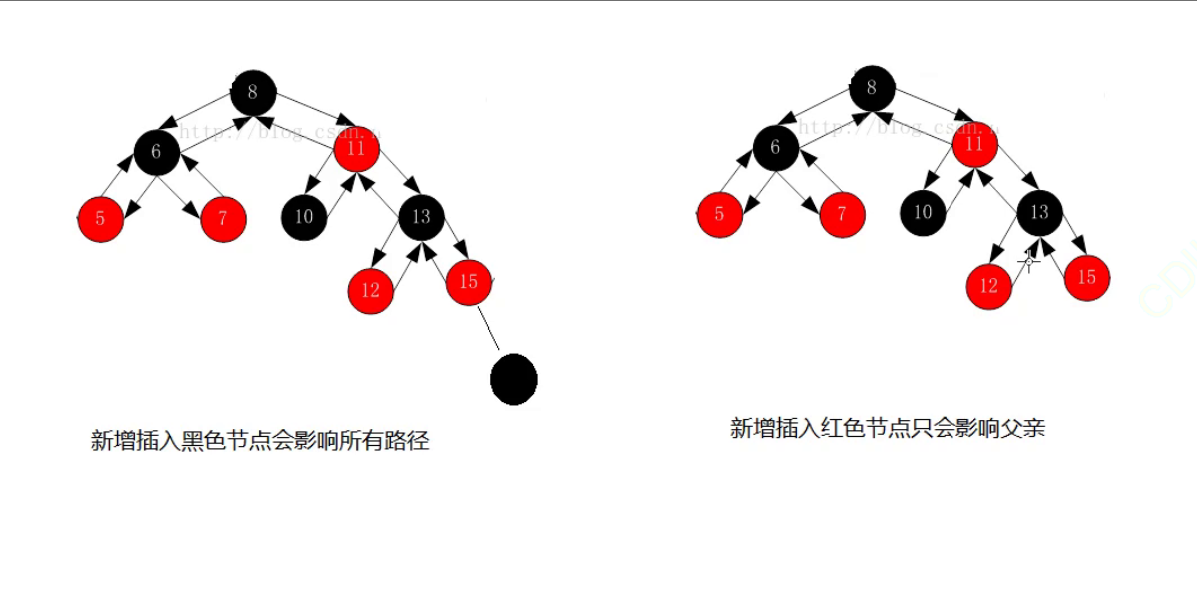
总结就是上图:这里就可以分类了,如果此时你在10(黑色)的下面插入一个红色节点,不需要任何的其它处理,此时并没有违反红黑树的任意一条规则。但是如果是在7(红色的后面增加了一个节点)

此时就违反了规则出现了连续的红色节点,需要进行处理。
所以对于一棵已经存在的红黑树,插入新节点时的颜色应该是红色,如果新增节点的颜色是黑色的那么就需要处理整颗树的所有的路径。
总结如果新增节点是红色的那么就有以下的情况:

这种情况不需要处理,因为新增节点的父节点是黑色的不需要任何的处理。
那么如果新插入节点的父节点是红色的呢?

我们知道AVL树的平衡因子是帮助我们去控制AVL树让其不成为一边倒的树(AVL树存在一些实现方法不需要平衡因子)。
那么当AVL树的平衡因子出现问题的时候,必然要处理的问题是旋转更改平衡因子。对于红黑树而言这里必要要处理更改的就是新增节点的父节点,必须更改为黑色。

这里就可以理解成,AVL树不平衡了更改平衡因子去处理,红黑树出现了两个红色节点的情况,那就通过变色去处理。
如果变颜色都无法处理,那就通过旋转+变色去处理。
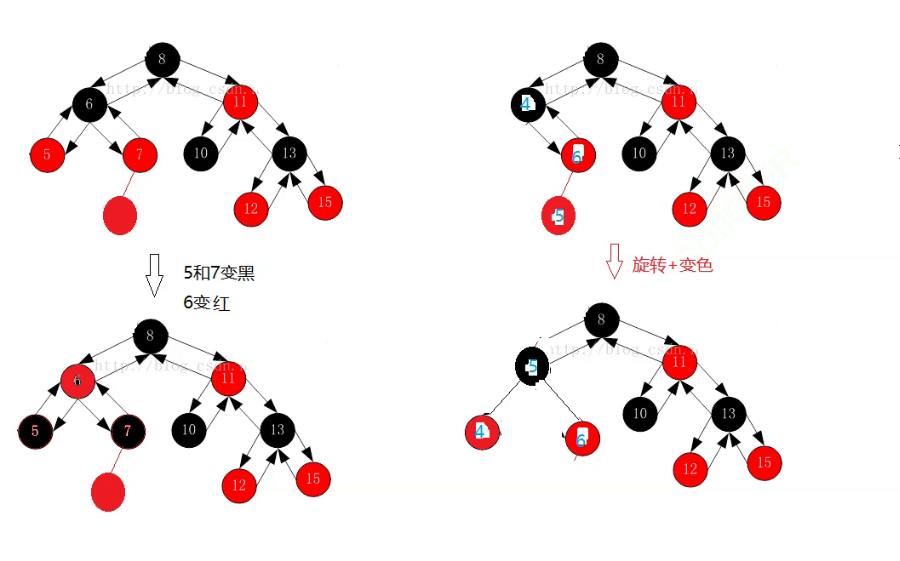
这里第一步肯定是通过将7变成黑色去处理两个红色一同出现的情况,但是这样又会导致7这一条路径多出现了一个黑色的节点,那么我们就可以去考虑将6给变红。
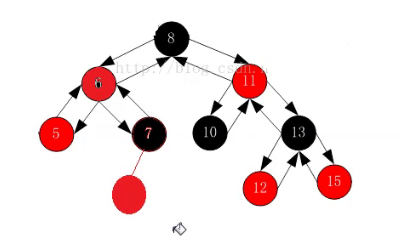
但是6变红又会导致5节点所在的2个路径少了一个黑色节点,就可以考虑将5给变成黑色。
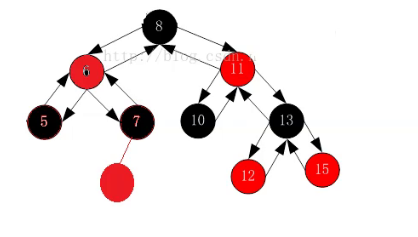
由此这里就解决了违反规则的情况。
此时不需要旋转。
那么如果是下面的这种情况呢?
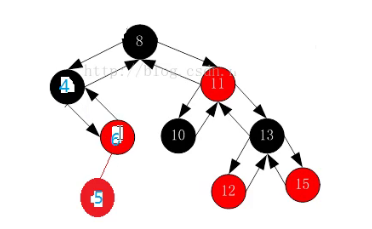
刚才是把5和7变成黑色,把6变成红色解决的问题(单纯的变色即可处理),但是现在如果没有右子树呢?
此时单纯的变色已经无法处理了。
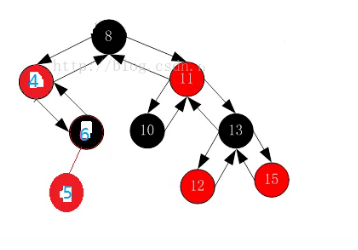
会发现4左边的路径少了一个黑色节点。
所以这个时候光变色已经无法处理了,需要进行一个右左双旋。
先以6为轴进行一个右旋,在以4为轴进行一个左旋。

此时在进行一个变色。
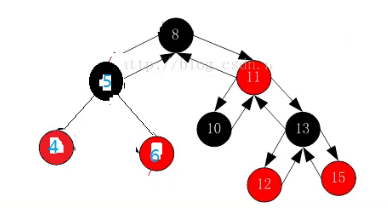
就可以解决问题。
总结就是下面的两种情况:
那么下面就来总结一下经过上面的流程得出的结论:

下面我们依旧是使用抽象图(因为会存在无数多种情况)来表示各种的情况:


这里的abcde和AVL树的抽象图一样可能是一个节点,也有可能是一棵红黑树也可能会空。
但是这里和AVL树不一样的是,这里abcde不谈高度,谈的是每条路径有多少个黑色的节点的红黑树的子树。
那么当遇到了两个红色节点连接在一起的时候,关键是去看什么呢?
这里的关键是去看uncle。
下面我们考虑一下上图中左边各个节点的颜色是否一定是那样的。
这个cur为新插入的节点为红色的,如果p为黑色不需要处理,但是此时我们分析的是需要处理的情况,所以p一定是红色的.因为在cur插入之前这里一定是一颗符合规则的红黑树,所以这里的g一定是黑色的,并且g一定是存在的(因为怕不可能是根(根一定是黑色的))。
那么下面就去看u
那么u存在且为红色

那么这里为什么要将g变成红色呢?变成黑色不行吗?
情况1:仅变色
祖父一定要变成红色,这里如果g就是整个红黑树的根,那么让g变成黑色是没有问题。但如果g只是一个局部子树的根,那么就相当于此时对于整颗红黑树而言,以g为根的子树凭空多了一个黑色的节点(g变成了黑色)。所以除非g为根节点,所以将g变成红色是为了保证整棵红黑树的黑色节点不变
需要继续往上调整的原因是g的父节点可能是一个红色。如果g的父是黑节点那就不需要再往上调整,但是g的父节点可能是一个红色,此时就要让g成为c,然后继续往上调整。直到最后遇到根节点。
那么下面我们来看一下情况1的具象图:
情况1:具象图1:cur自己就是新增

情况1:具象图2:cur的子树上存在新增
在a和b的任意子位置新增一个子节点。

那么cde的情况又是怎么样的呢?一定是下面四种情况的任意一种:
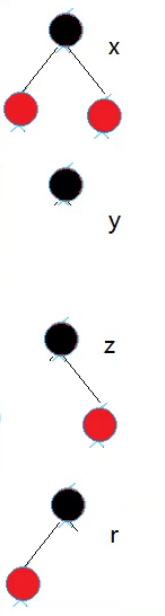
这里谈论的是具有几个黑色节点的红黑树。cde是每条路径一个黑色节点的红黑树(共存在4种)a和b是一个红色节点。
此时针对于具象图1我们要如何处理呢?

首先我们将a和b变成黑色,将cur变成红色:
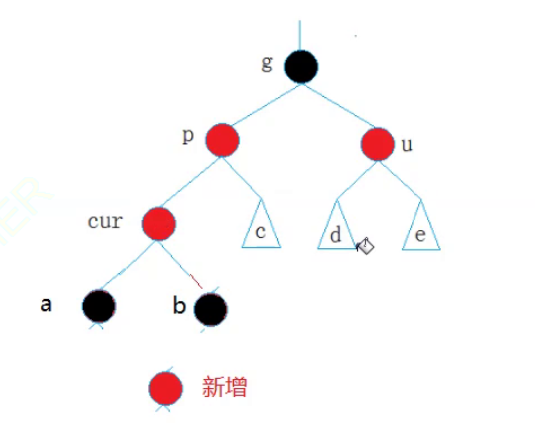
此时cur和p再次成为连续的红色节点,那么我们再将p和u变成黑色,再将g变成红色

那么在这种具象图的时候cur新增一开始应该在什么地方呢?
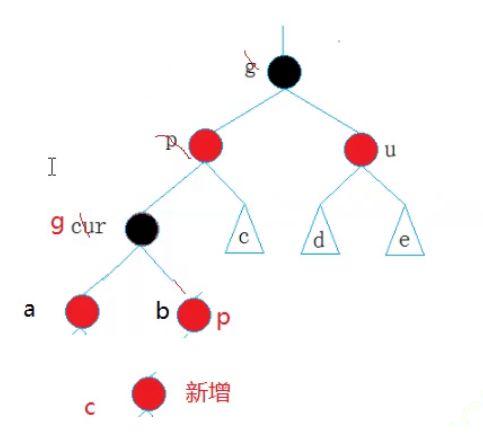
a也就是uncle。就拿这个具象图2来分析一下:
cde具有4种形态也就是4*4*4
在加上c的新增也具有4种情况
那么总情况就是4*4*4*4 = 256种。
这还只是增加了一层,如果在增加一层,首先cde就是每条路径具有两个黑色节点的红黑树,那么数量可以说是很多的。
以下是一个每条路径具有两个黑色节点的红黑树

此时最顶层的节点都是可以删除的,也是能够保留一些的。可以说数量是很恐怖的。
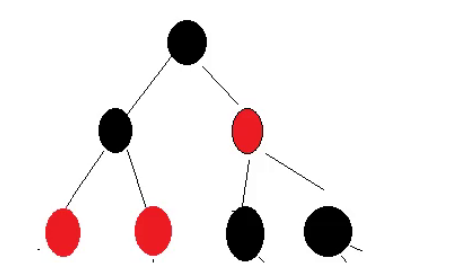
这也是每条路径具有两个黑色节点的红黑树
同样这也是
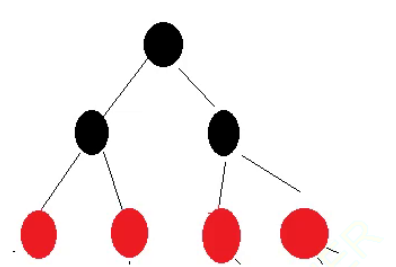
以上的这些情况都可以作为cde的子树(这还只是很少的一部分,即每条路径都存在2个黑色节点的红黑树)。
所以我们需要使用抽象图。
不管此时的情况是由下面的一层还是两层变过来的,我都不管。都是一样的,只要不断循环往上变色即可。我们对于情况1的处理方式都是:
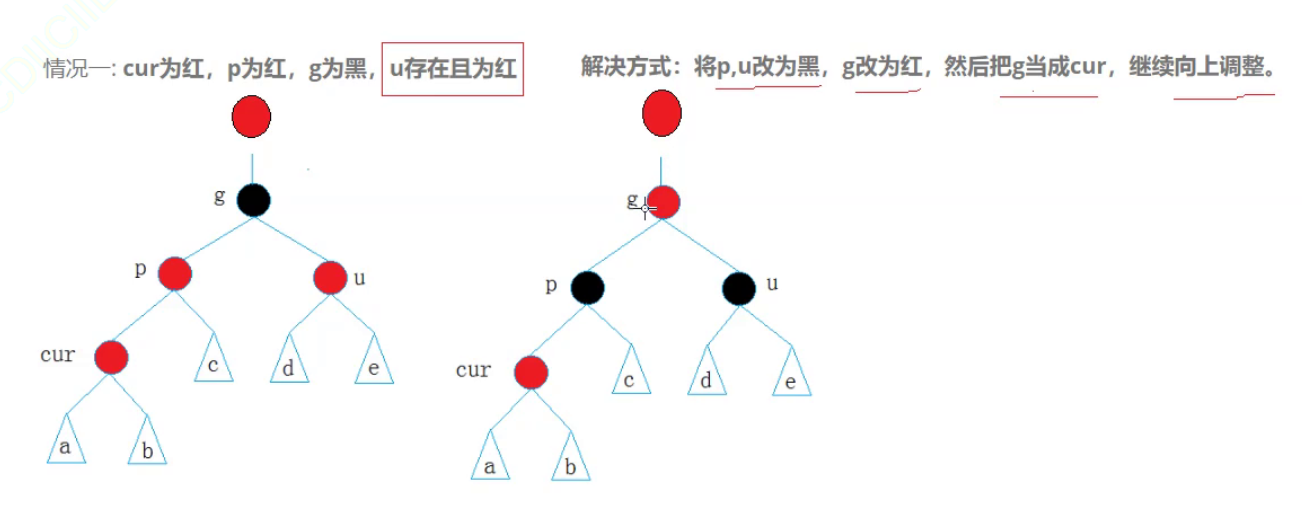
把p和u变成黑色g变成红色,再往上去变色。
以上是一种情况:
情况2:单旋转+变色
下一种情况:
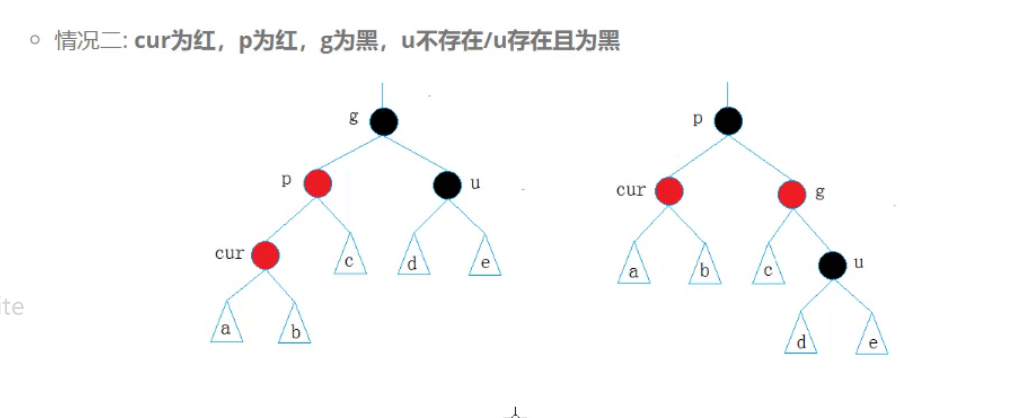
依旧是去看u,如果u不存在或是为黑又是一种情况。
首先如果u不存在。
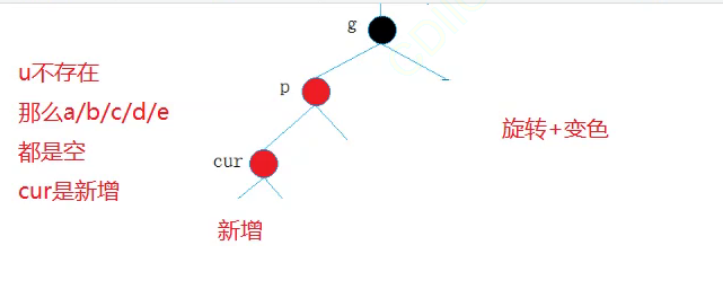
此时一个右旋+变色即可处理。
如果u存在且为黑色,那么u一定是由下面变色边上来的。
此时能够确定下面的结论:

c需要去补一个黑色节点,那么d和e要么是空要么是红色。
此时的情况就有4*2*2种情况。
此时第一种情况往上更新的时候,可能会变成第一种情况(继续往上更新),也有可能会变成第二种情况(需要旋转+变色)。
下面我们就来总结上面的结论:
第一个

这里通过维护那5个维泽保证了红黑树是近似平衡
第二个:

对于处理也是大体分成两种情况的:
总结1

总结:仅变色情况
情况1:uncle节点存在为红(因为其它几个节点(gpc)的颜色是固定的,c为红色(新插入,或者下面调整上来{原因在上面说过了}),p一定是红色,那么g一定是黑色。)

总结:需要旋转的情况
情况2:uncle节点不存在/u存在为黑色
我们来看情况2的第一种如果uncle是不存在的。
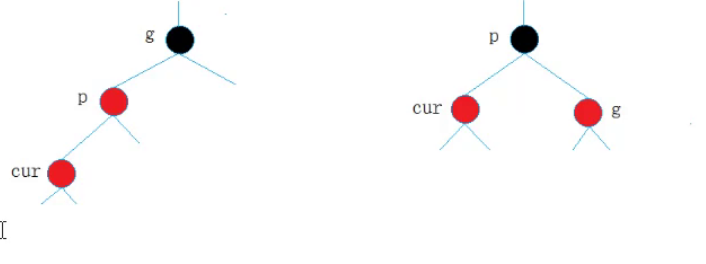
此时的cur就是新增解决方式也很简单就是一个左旋(以g为轴)即可
下面是情况2的第二种如果uncle是存在且为黑色的。
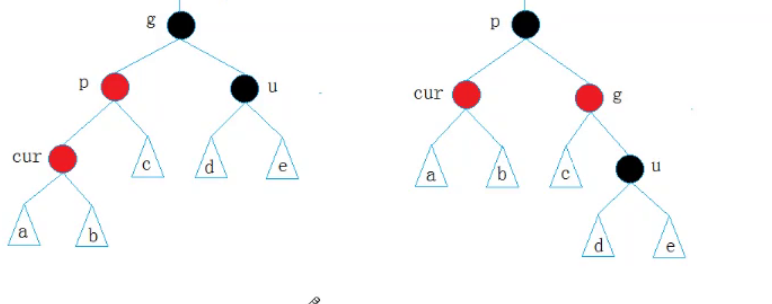
此时的cur就不是新增了,因为cur的变色是在a或者b的下面新增然后通过变色不断影响上来的。下面我们假设右子树只存在u这一个黑色节点
c就是只包含一个黑色节点的红黑树(4种情况)
新增应该是这里

总结在情况2:cur存在且为黑色的情况,并且每条路径只存在1个黑色节点的情况下具象图情况:
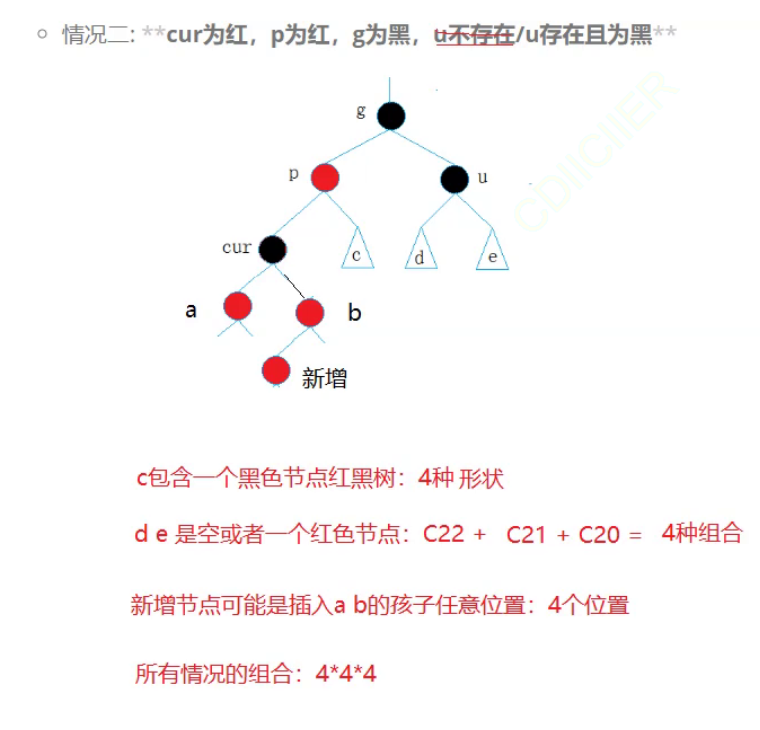
存在64种。但是我们不管这种具象图有多少种,我们的解决方式都是进行一个左旋+变色:
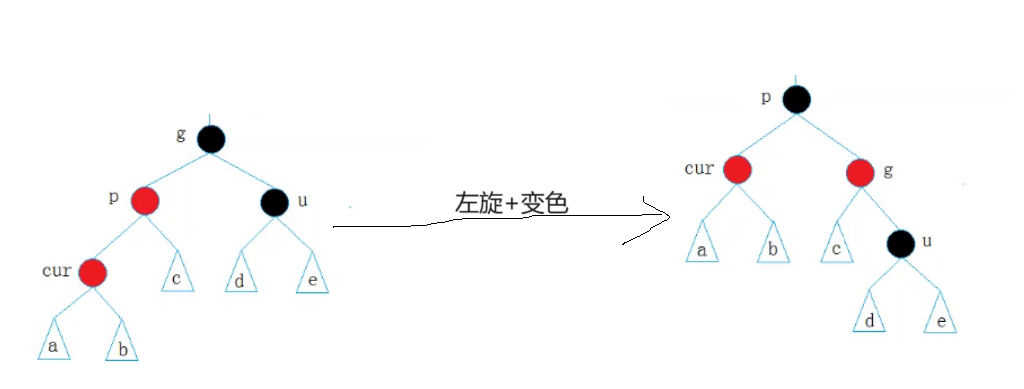
将p变成黑色,cur和g变成红色
这里思考一个问题将cur和g变成黑色,p变成红色可吗?
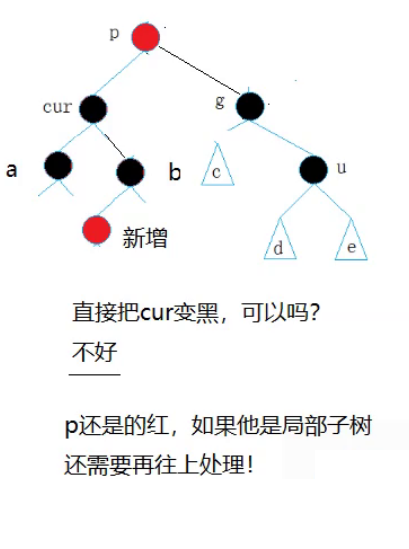
即此时的p不是一个终结态,所以这里p应该成为黑色让其成为一个终结态。
总结旋转的解决方案:

以上都是单旋转的情况。
总结:双旋转
下面是双旋转的情况此时的u是不存在/存在但是黑色的。然后如果此时的cur是p的左孩子,但是p是grandfather的右孩子。
此时需要的就是右左双旋。
如果此时的cur是p的右孩子,但是p是grandfather的左孩子,此时就需要左右双旋转。
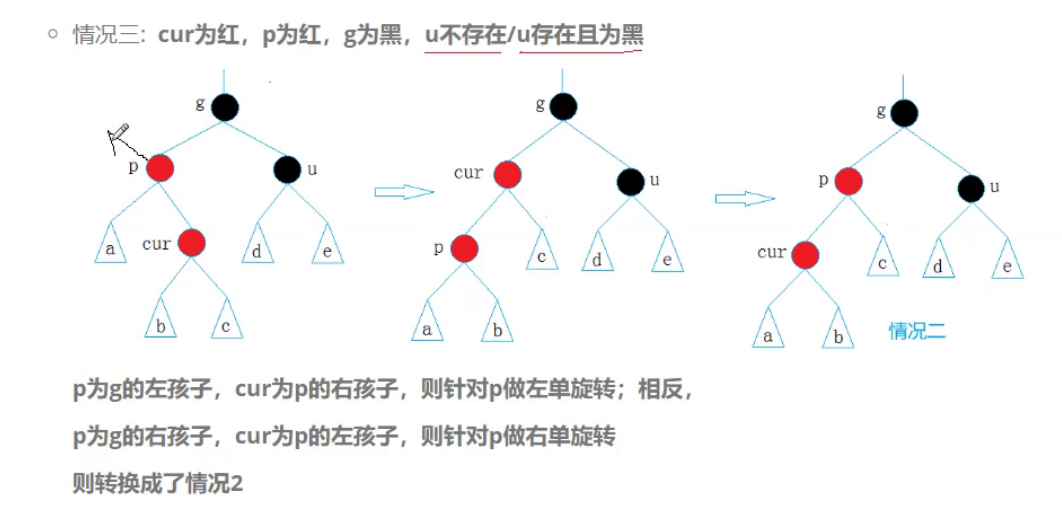
可以看到此时p是g的左孩子,但是c是p的有孩子,此时就需要首先以p为轴进行一个左旋转。再以g为轴今昔那个一个右旋转。最后再加上变色。
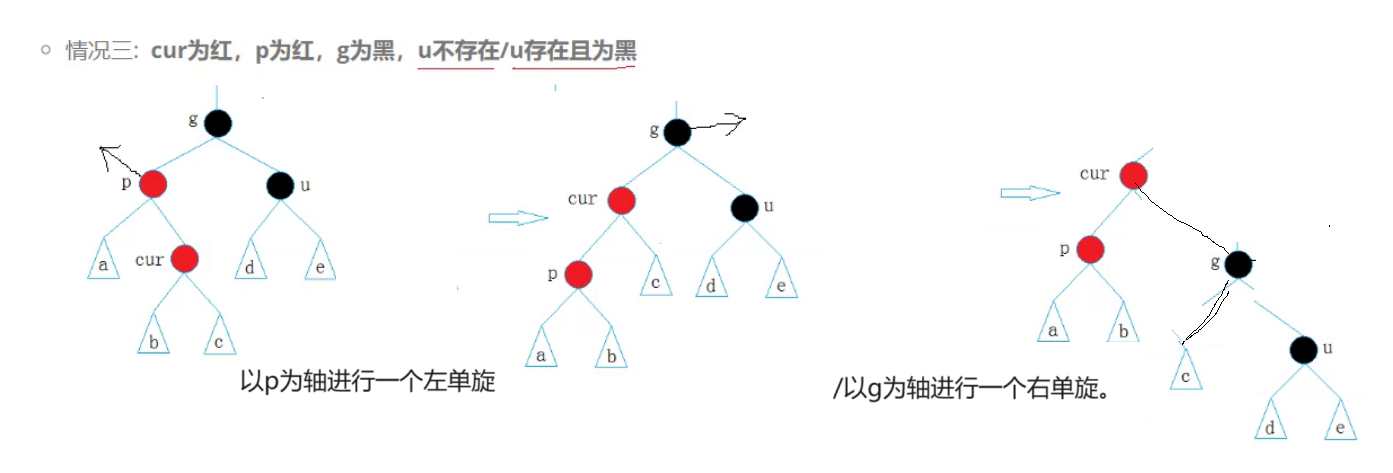
然后修改颜色:

cur修改为黑色,g修改为红色
对于这种情况如果u是不存在呢?

解决方法还是不变依旧是先进行一个左旋再进行一个右旋。然后修改颜色
以上就分析完了uncle处于g的右边的情况,然后还存在一个大的情况那就是uncle在grandfather的左边。
然后依旧是cur和p位于右边,然后根据u的颜色分类,u为黑色(旋转+变色{}),u为红色(变色+往上继续处理)。
抽象图:
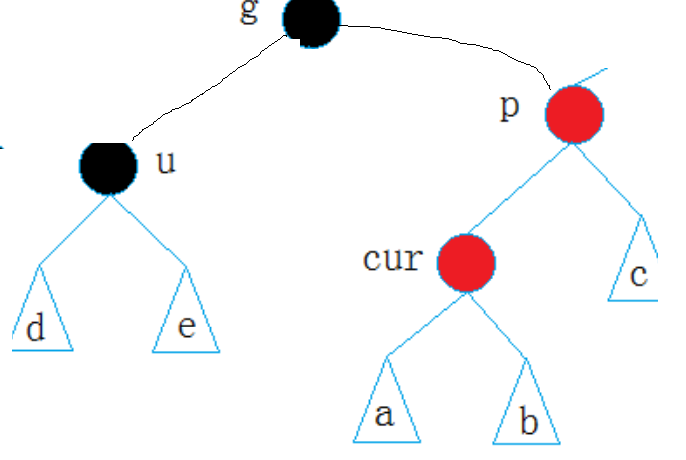
处理方式和在左边是一样的唯一不同也就是在于旋转了,例如上图此时要进行的就是先一个右旋(parent为轴),在一个左旋转(grandparent为轴)。
单旋转图:

进行一个单独的左旋(以g为轴)即可。旋转后变色的方案依旧是不变的
结果就是下图(双旋转后+变色)
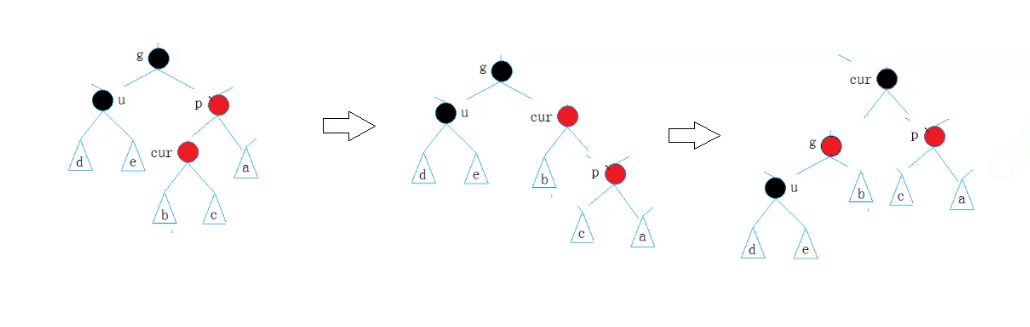
依据上面的学习我们就能够将一棵红黑树构建出来了,但是如何判断这颗二叉树就是红黑树呢?(AVL树可以通过求高度相减的方式得到,但是红黑树应该怎判断呢?)
这里我们选择的是去检测规则三:

验证红黑树
总的来说验证红黑树其实就是验证两个规则一个就是验证不能存在连续的红色节点,以及每条路径的黑色节点的个数是相同的。
那么如何去检测呢?
这里如果我遇到一个父节点是红色节点,然后去检测孩子是否是黑色的这种方式很不好检查。这里我们就可以换一个思路去检擦:如果当前节点是红色的,那么就去看父节点如果父节点是红色,那么就相当于出现了连续的红色节点,破坏了规则直接返回false即可。
这个方法比遇到一个红色节点去检查孩子是很好的,因为孩子节点是存在两个的,但是父节点对于一个节点而言是只存在一个的。
但是以上的规则都是检测是否存在红色节点的,并没有检测到每条路径的黑色节点的个数,每条路径黑色节点的个数我们需要怎么去检测呢?
我们可以使用一个常量来表示黑色节点的个数:但是在递归的时候,不能使用引用
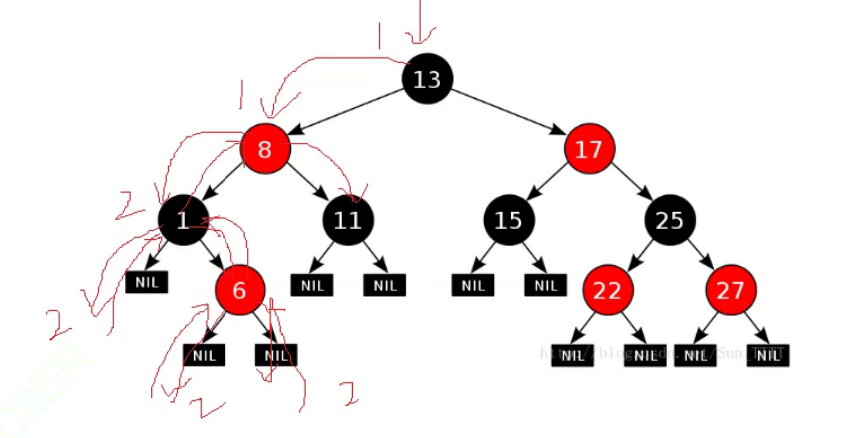
例如上面当读取到13节点的时候,常量为1,而在读取到1节点的时候常量为2,然后就遇到null了返回2了,同理对于6号节点也是2进去然后返回,再将1节点路径上的黑色节点个数判断完成之后,回到8号节点,在去8号节点的右边寻找黑色节点,这里不使用引用的好处也就出来了。此时这里的常量为1,然后去到11号节点后才会成为2.
这就是使用引用的好处
你可以认为这个常量记录的是:

但是依靠打印然后我们人眼去看,这样在数据极其多的时候,是看不过来的,所以这里我们还有一个方法就是将每一条路径的黑色节点个数使用一个vectror储存起来,然后在遍历完红黑树之后,遍历一下vector,检测是否出现黑色节点个数不同的情况。但是还有一个方法就是我们只用将每一次获取到的值(黑色节点的个数)和一个标准去比较也是一个方法。
下面是检测的代码:
bool IsBalance()
{
if (_root == nullptr)
return true;
if (_root->_color == RED)
return false;
//参考值
int refVal = 0;
Node* cur = _root;
while (cur)
{
if (cur->_color == BLACK)
{
++refVal;
}
cur = cur->_left;
}//在这里计算一条路径的黑色节点的个数
int blacknum = 0;
return Check(_root, blacknum, refVal);
}
bool Check(Node* root, int blacknum, const int refVal)
{
if (root == nullptr)
{
//cout << balcknum << endl;
if (blacknum != refVal)//判断是否和参考值是否一样
{
cout << "存在黑色节点数量不相等的路径" << endl;
return false;
}
return true;
}
if (root->_color == RED && root->_parent->_color == RED)
{
cout << "有连续的红色节点" << endl;
return false;
}
if (root->_color == BLACK)
{
++blacknum;
}
return Check(root->_left, blacknum, refVal)
&& Check(root->_right, blacknum, refVal);
}红黑树插入的代码
struct RBNode
{
RBNode<K, T>* _left;
RBNode<K, T>* _right;
RBNode<K, T>* _parent;
pair<K, T> _kv;//这里依旧是采用经典的红黑树节点的
Color _color;
RBNode(const pair<K,T>&V)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(V)
,_color(RED)
{}//这里我们就设定了当我在一棵红黑树上插入的时候,插入的节点首先应该是红色。
};
template<class K,class T>
class RBTree
{
public:
typedef RBNode<K, T> Node;
bool Insert(const pair<K, T>& t)
{
//首先第一步依旧是按照搜索树的规则找到要插入的节点
if (_root == nullptr)
{
_root = new Node(t);//此时的树是一棵空树,直接创建一个空间然后返回即可
_root->_color = BLACK;//保证插入的根节点是一个黑色的节点
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_kv.first < t.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > t.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;//代表之间已经插入过一个相同的值了直接返回false即可
}
}
//到这里就找到了t应该在的位置
cur = new Node(t);//新插入节点的颜色是红色的
cur->_color = RED;//新增节点给红色
//下面需要将新增节点链接到整棵树上
if (parent->_kv.first < cur->_kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//下面需要去看父节点的颜色
while (parent&&parent->_color == RED)// 如果此时父节点的颜色是红色则需要去处理,因为parent可能为空所以这里也需要判断一下
{
Node* grandfather = parent->_parent;
if (parent == grandfather->_left)//父节点是祖父节点的左孩子,那么uncle节点就是祖父的右孩子
{
Node* uncle = grandfather->_right;
//下面根据uncle节点的状态来分类
if (uncle && uncle->_color == RED)// uncle节点存在并且为红色
{
//变色
parent->_color = uncle->_color = BLACK;
grandfather->_color = RED;//将p和u变成黑色,然后将g变成红色,继续往上处理
cur = grandfather;
parent = grandfather->_parent;//这里就存在一个需要我们处理的问题,如果这里的grand就是根节点,那么parent就为空
//同时也就带来了一个问题,如果parent不存在,那么我们需要将grandfather变成黑色。怎么处理呢?难道还是需要特判一下?
}
else//uncle节点不存在,或者存在但是是黑色的
{
//下面就是判断需要使用哪一种旋转方式
//单旋转。
if (cur == parent->_left)//此时这里就是p为g的左孩子,而c为p的左孩子
{
RotateR(grandfather);//以grandfather为轴进行一个右旋转
//旋转完成之后要进行一个变色
parent->_color = BLACK;
grandfather->_color = RED;
break;//在完成之后就可以直接跳出循环了
}
else//此时的p为g的左孩子,但是c为p的右孩子
//
// g
// p u
// c
{
//此时就需要进行一个双旋转
RotateL(parent);//以parent为轴进行一个左旋转
RotateR(grandfather);//再以grandfather为轴进行一个右旋转。
//最后是变色
cur->_color = BLACK;
grandfather->_color = RED;
break;//这里必须使用一个break跳出因为通过双旋转最后的效果图
//我们知道如果不改变p的指向那么p就是一个红色的,还是会进入循环
//所以这里直接跳出循环
}
}
}
else// uncle节点是祖父节点的左孩子,两者的不同就在于解决时的旋转方式不同
{
Node* uncle = grandfather->_left;//uncle为g的左孩子
//依旧是按照uncle的状态来分类
if (uncle && uncle->_color == RED)//存在且为红色
{
//变色
parent->_color = uncle->_color = BLACK;
grandfather->_color = RED;
cur = grandfather;
parent = grandfather->_parent;//继续向上处理
}
else//uncle节点不存在/存在但是是黑色
{
if (cur == parent->_right)
{
//单选转即可
RotateL(grandfather);
grandfather->_color = RED;
parent->_color = BLACK;
//这里可以不需要写break因为循环的条件就是parent必须为红色,才会进入循环
}
else
{
//需要双旋转
RotateR(parent);
RotateL(grandfather);
cur->_color = BLACK;
grandfather->_color = RED;
break;//这里需要增加一个break,防止出现再次进入循环的现象
}
}
}
}
_root->_color = BLACK;//这里来解决上面的那个问题(如果g被变色后发现是根节点,需要重新变成黑色,那么_root这个指针一定是指向g的最后在这里解决一下即可)
// 这里的逻辑是很巧妙的
return true;
}
void RotateR(Node* parent)//完成一个右旋
{
Node* parent_parent = parent->_parent;//用于旋转之后的链接
Node* subleft = parent->_left;
Node* subleftR = subleft->_right;
parent->_left = subleftR;
if (subleftR)//这个节点是可能不存在的
subleftR->_parent = parent;//改变一个节点之后,不要忘了需要改变父节点
subleft->_right = parent;
parent->_parent = subleft;
subleft->_parent = parent_parent;
//以上都是完成的旋转的工作下面完成和整体二叉树的链接工作
if (_root == parent)
{
_root = subleft;
subleft->_parent = nullptr;
}
else
{
if (parent_parent->_left == parent)
{
parent_parent->_left = subleft;
}
else
{
parent_parent->_right = subleft;
}
}
}
void RotateL(Node* parent)//完成一个左旋
{
Node* parent_parent = parent->_parent;
Node* subright = parent->_right;
Node* subrightL = subright->_left;
parent->_right = subrightL;
if (subrightL)
subrightL->_parent = parent;
subright->_left = parent;
parent->_parent = subright;
//以上都是完成的旋转,下面是链接
if (_root == parent)
{
_root = subright;
subright->_parent = nullptr;
}
else
{
if (parent_parent->_left == parent)
{
parent_parent->_left = subright;
subright->_parent = parent_parent;
}
else
{
parent_parent->_right = subright;
subright->_parent = parent_parent;
}
}
}
void Inorder()
{
_Inorder(_root);
}
bool IsBalance()
{
if (_root == nullptr)
return true;
if (_root->_color == RED)
return false;
//参考值
int refVal = 0;
Node* cur = _root;
while (cur)
{
if (cur->_color == BLACK)
{
++refVal;
}
cur = cur->_left;
}//在这里计算一条路径的黑色节点的个数
int blacknum = 0;
return Check(_root, blacknum, refVal);
}
bool Check(Node* root, int blacknum, const int refVal)
{
if (root == nullptr)
{
//cout << balcknum << endl;
if (blacknum != refVal)//判断是否和参考值是否一样
{
cout << "存在黑色节点数量不相等的路径" << endl;
return false;
}
return true;
}
if (root->_color == RED && root->_parent->_color == RED)
{
cout << "有连续的红色节点" << endl;
return false;
}
if (root->_color == BLACK)
{
++blacknum;
}
return Check(root->_left, blacknum, refVal)
&& Check(root->_right, blacknum, refVal);
}
private:
void _Inorder(Node* root)
{
if (root == nullptr)
{
return;
}
_Inorder(root->_left);
cout << root->_kv.first << endl;
_Inorder(root->_right);
}
Node* _root = nullptr;
};然后我验证的思路是使用随机数的方法来解决的这个问题。
代码:
int main()
{
const int N = 1000000;
vector<int> v;
v.reserve(N);
//srand(time(0));
for (size_t i = 0; i < N; i++)
{
v.push_back(rand() + i);
//cout << v.back() << endl;
}
size_t begin2 = clock();
RBTree<int, int> t;
for (auto e : v)
{
if (e == 19173)
{
int i = 0;
}
t.Insert(make_pair(e, e));
//cout << "Insert:" << e << "->" << t.IsBalance() << endl;
}
size_t end2 = clock();
cout << "Insert:" << end2 - begin2 << endl;
cout << t.IsBalance() << endl;
return 0;
}运行截图:
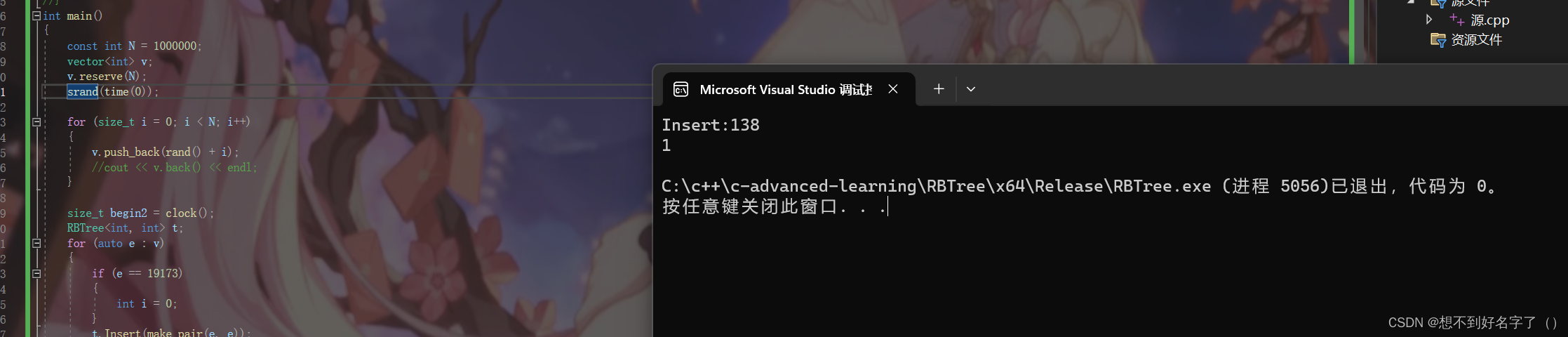
希望这篇博客能对你有所帮助,写得不好请见谅。如果发现了任何的错误,欢迎指出。我一定改正。