Java必刷入门递归题×5（内附详细递归解析图）

news2025/1/9 1:50:19

1.求N的阶乘

2.求1+2+...+N的和

3.顺序打印数字的每一位

4.求数字的每一位之和

5.求斐波拉契数列

1.求N的阶乘

（1）解析题目意思

比如求5的阶乘，符号表示就是5！；所以5！=5*4*3*2*1
我们下面使用简单的递归完成本题，看递归代码

public static int sub(int n) {
        if(n==1) {
            return 1;
        }
        return n * sub(n-1);
    }

下面解析该代码的意思

（2）递归思路

拆解算法：6！=6*5！；5！=5*4！；4！=4*3！；3！=3*2！；2！=2*1！；其实也就是6！=6*5*4*3*2*1。
用代码表示：整体可能有点乱，需要读者静下心来理解

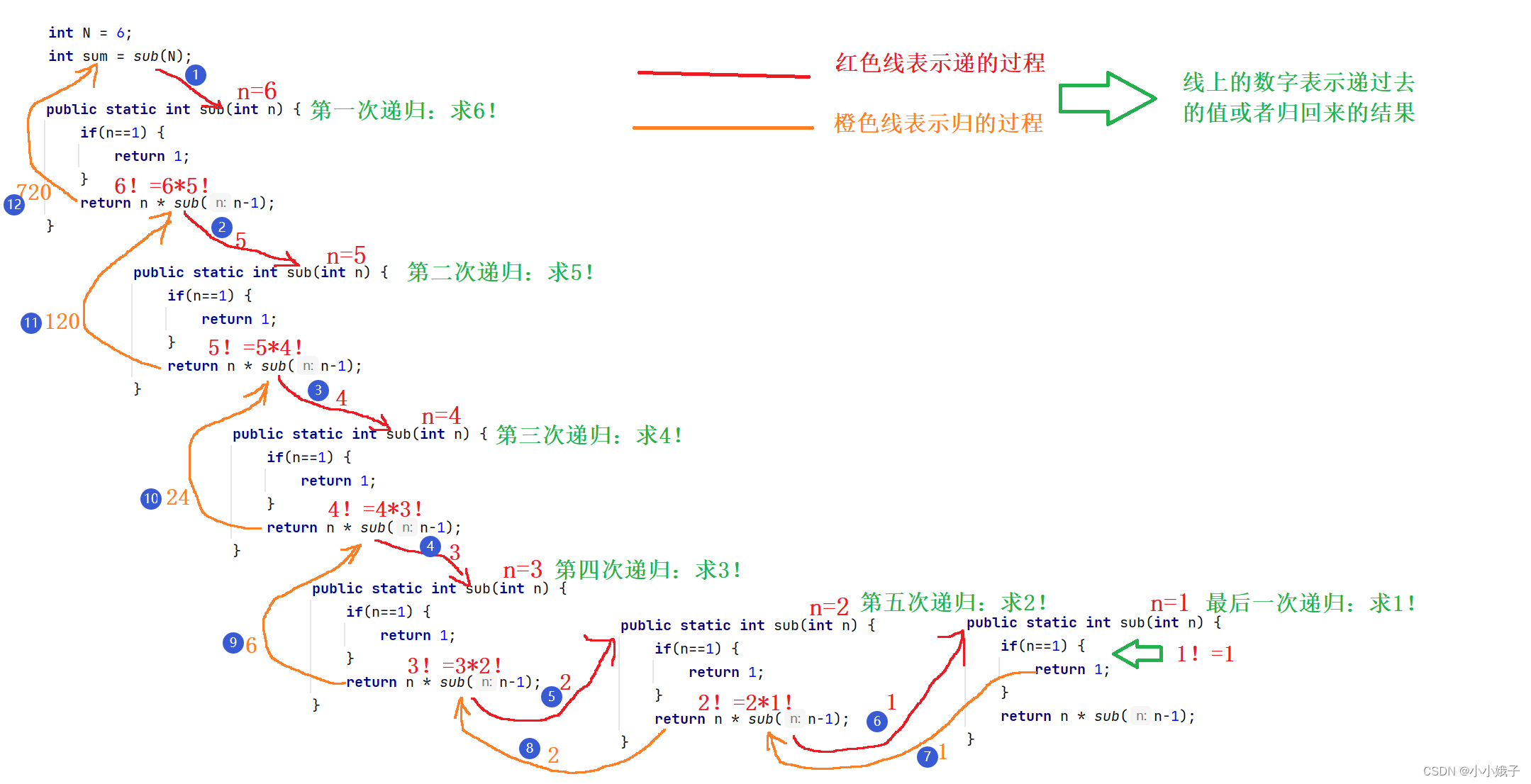
（3）完整代码

public static void main3(String[] args) {
        //递归求N的阶乘  
        int N = 6;
        int sum = sub(N);
        System.out.println(sum);
    }
    public static int sub(int n) {
        if(n==1) {
            return 1;
        }
        return n * sub(n-1);
    }

2.求1+2+...+N的和

（1）解析题目意思

假设N=3，意思是求从1加到N的和（1+2+3）
假设N=4，则需要求（1+2+3+4）的和

（2）递归思路

我们这里以N=3举例
思路：求（1+2+3）可以拆解成：3+（求N=2的和），求N=2的和可以拆解成：2+（求N=1的和）
得出递归代码

public static int sum(int n) {
        if(n==1) {
            return 1;
        }
        return n+sum(n-1);
    }

下面剖解递归思路：

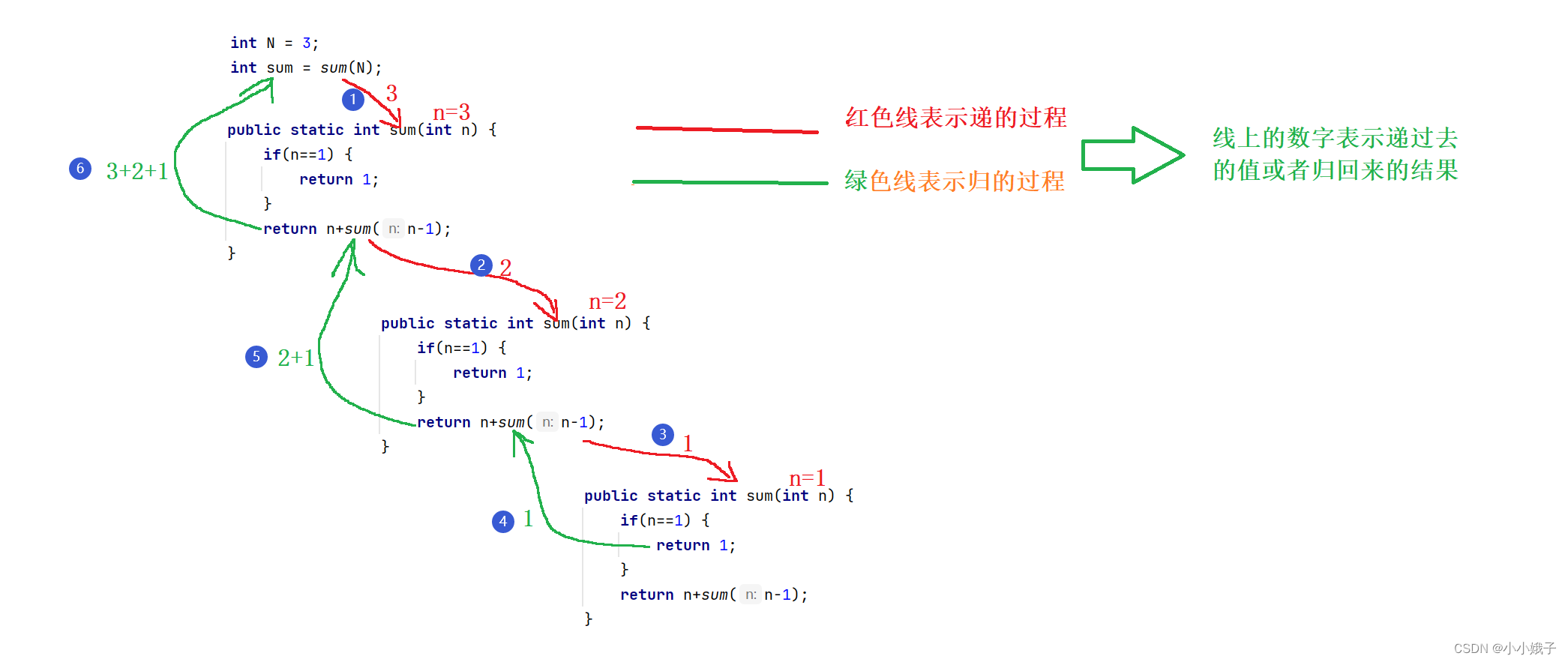
（3）完整代码

 public static void main(String[] args) {
        //递归求和
        int N = 3;
        int sum = sum(N);
        System.out.println(sum);
    }
    public static int sum(int n) {
        if(n==1) {
            return 1;
        }
        return n+sum(n-1);
    }

3.顺序打印数字的每一位

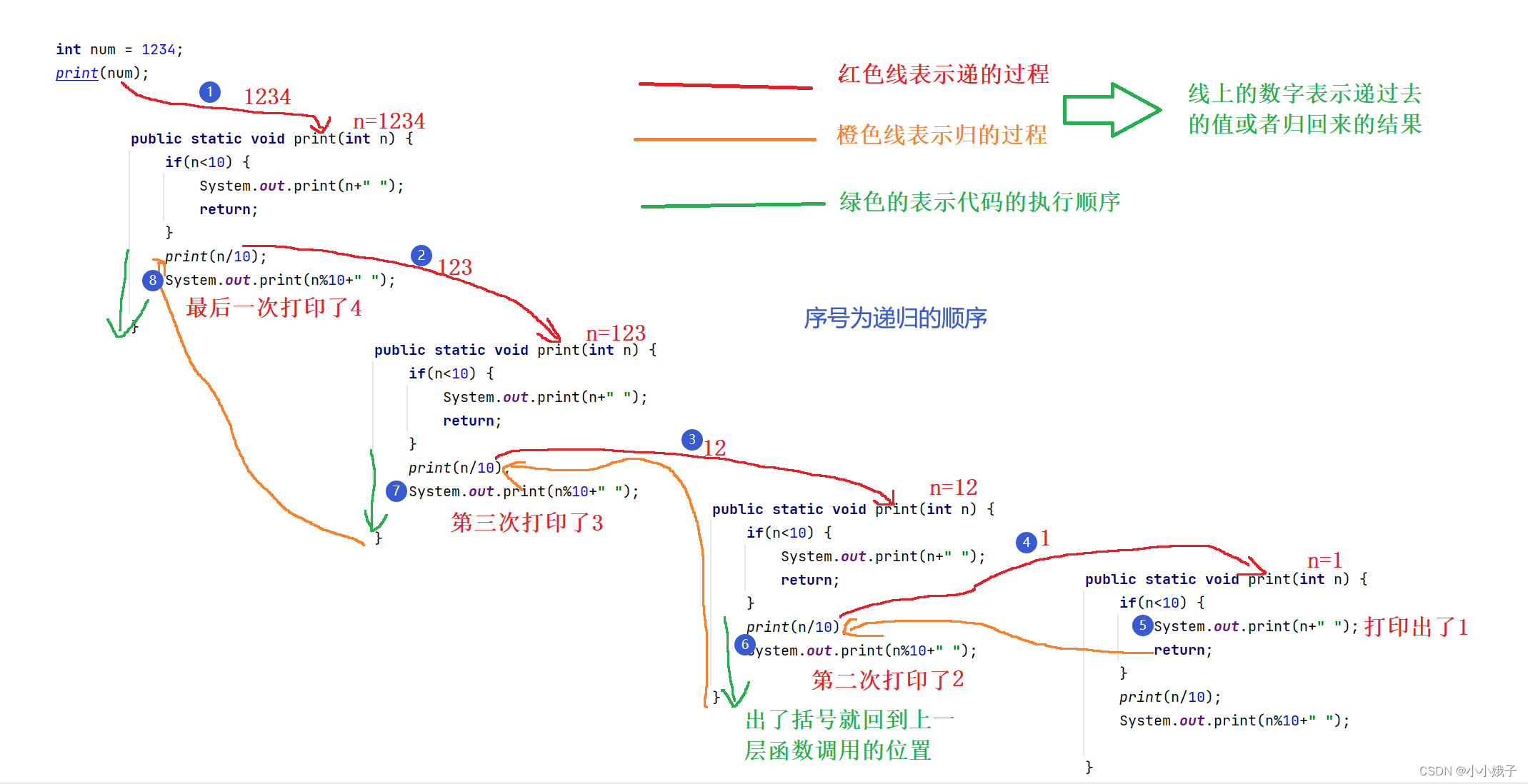
（1）解析题目意思

比如打印1234，要题目意思打印的结果就是1 2 3 4（中间隔开）

（2）解析递归思路

假设输入的数据是1234,打印出1 2 3 4
思路：要打印1 2 3 4，就要先打印1 ，再打印2 3 4 ；打印2 3 4 ，就要先打印2 ，再打印3 4 ；打印3 4，就要先打印3 ，再打印4
利用/10去掉最低位，%10得到最低位的思路进行
得出递归代码

 public static void print(int n) {
        if(n<10) {
            System.out.print(n+" ");
            return;
        }
        print(n/10);
        System.out.print(n%10+" ");

    }

解析递归思路

（3）完整代码

public static void main(String[] args) {
        //顺序打印数组的每一位
        int num = 1234;
        print(num);
    }
    public static void print(int n) {
        if(n<10) {
            System.out.print(n+" ");
            return;
        }
        print(n/10);
        System.out.print(n%10+" ");

    }

4.求数字的每一位之和

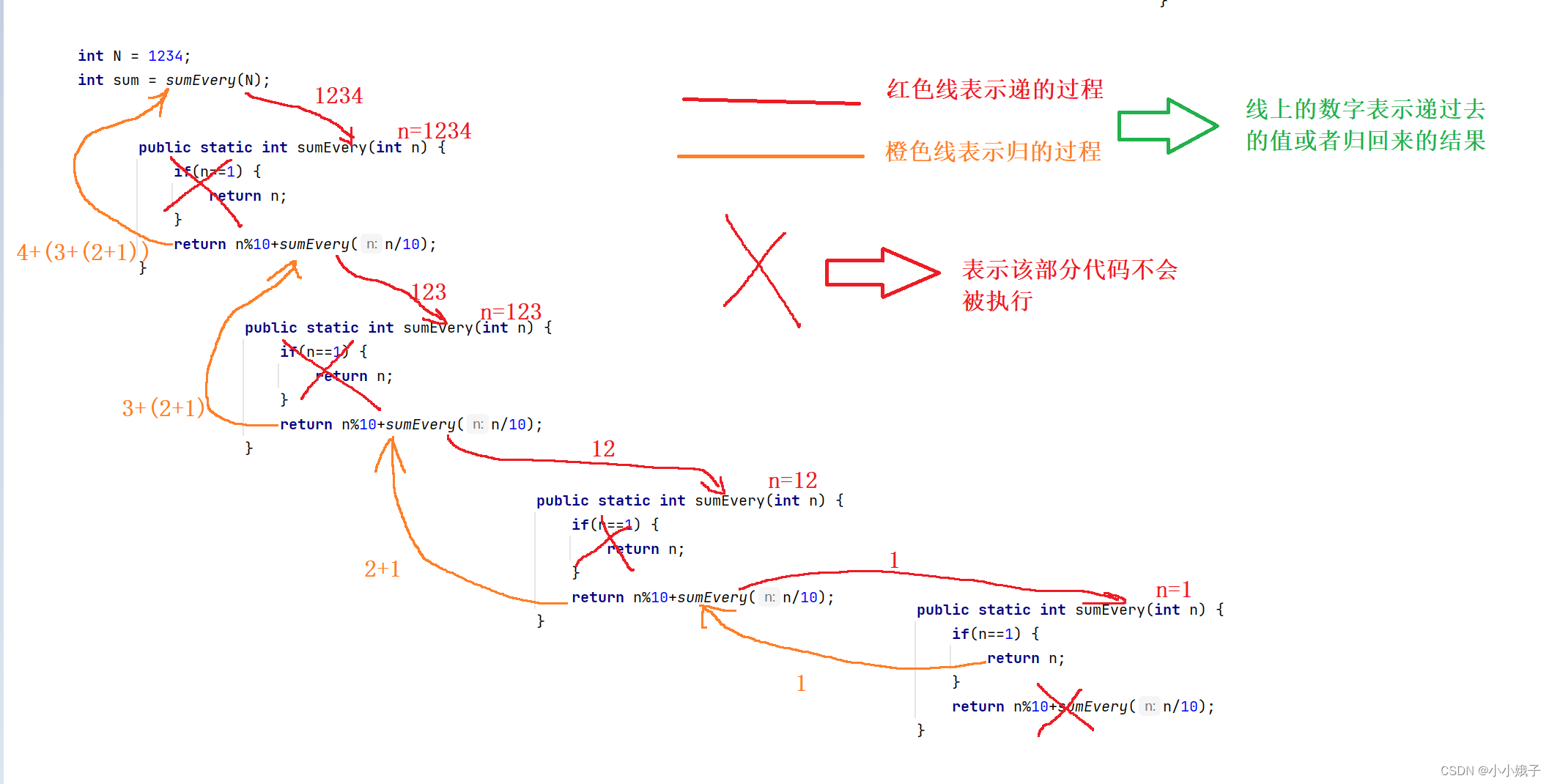
（1）解析题目

比如给出数字：1345，就需要求1+3+4+5的和

（2）解析递归思路

我们这里以求1234的每一位之和
同样利用/10去掉最低位，%10得到最低位的思路
思路：求1234的每一位之和，可以求4+123的每一位之和；求123的每一位之和，可以求3+12的每一位之和；求12的每一位之和，可以求1+2的每一位之和
递归代码

 public static int sumEvery(int n) {
        if(n==1) {
            return n;
        }
        return n%10+sumEvery(n/10);
    }

递归过程解析

（3）完整代码

public static void main(String[] args) {
        //求数字的每一位之和
        int N = 1234;
        int sum = sumEvery(N);
        System.out.println(sum);
    }
    public static int sumEvery(int n) {
        if(n==1) {
            return n;
        }
        return n%10+sumEvery(n/10);
    }

5.求斐波拉契数列

（1）了解斐波拉契数列

斐波那契数列，其数值为：1、1、2、3、5、8、13、21、34……这个数列从第3项开始，每一项都等于前两项之和。

（2）递归思路求解

比如求第五个斐波那契数（5）：5=3（第四个数）+2（第三个数）；3=2（第三个数）+1（第二个数）；以此类推，直到n<=2。
递归部分代码

 public static int fib(int n) {
        if(n<=2) {
            return 1;
        }
        return fib(n-2)+fib(n-1);
    }

递归思路解析

递归完整代码

 public static void main(String[] args) {
        //斐波拉契
        int N = 8;
        int sum = fib(N);
        System.out.println(sum);
    }
    public static int fib(int n) {
        if(n<=2) {
            return 1;
        }
        return fib(n-2)+fib(n-1);
    }

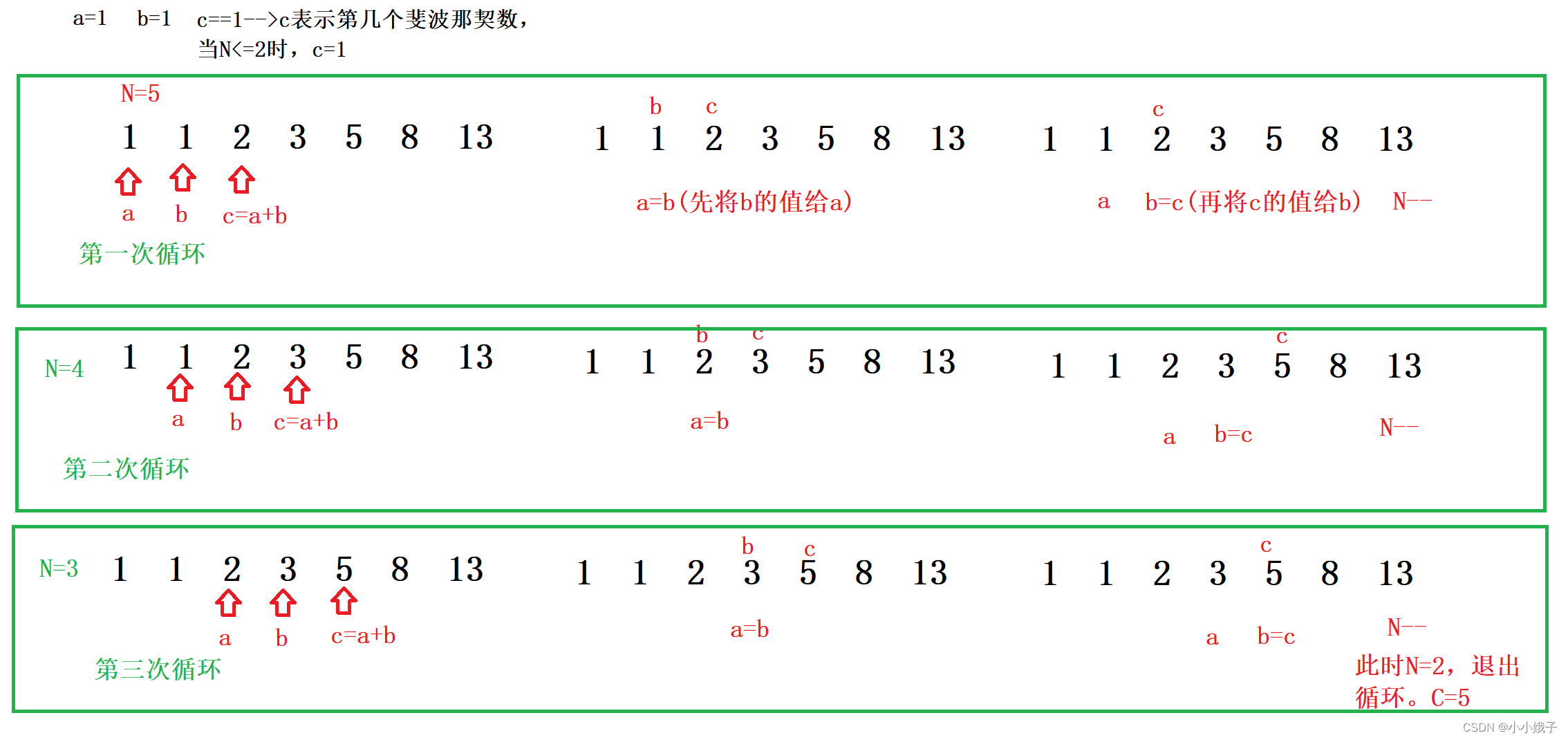
（3）迭代思路

该思路也就是利用循环去做，可以计算更大的斐波那契数
利用：某个数=前面两个数相加，从前面开始往后计算，不断循环即可
代码展示：

 public static void main(String[] args) {
        //迭代思路
        int N = 5;
        int a = 1;
        int b = 1;
        int c = 1;
        while(N>2) {
           c = a+b;
           a = b;
           b = c;
           N--;
        }
        System.out.println(c);
    }