＜C++＞ stack queue模拟实现

目录

前言

一、stack的使用

1. 接口说明

2. 例题

二、模拟实现stack

三、queue的使用

四、模拟实现queue

五、deque

总结

前言

LIFO stack

1. 栈是一种容器适配器，专门设计用于在后进先出上下文（后进先出）中运行，其中元素仅从容器的一端插入和提取。

2. stack 作为容器适配器实现，容器适配器是使用特定容器类的封装对象作为其底层容器的类，提供一组特定的成员函数来访问其元素。元素从特定容器的“背面”推出/弹出，这被称为堆栈的顶部。

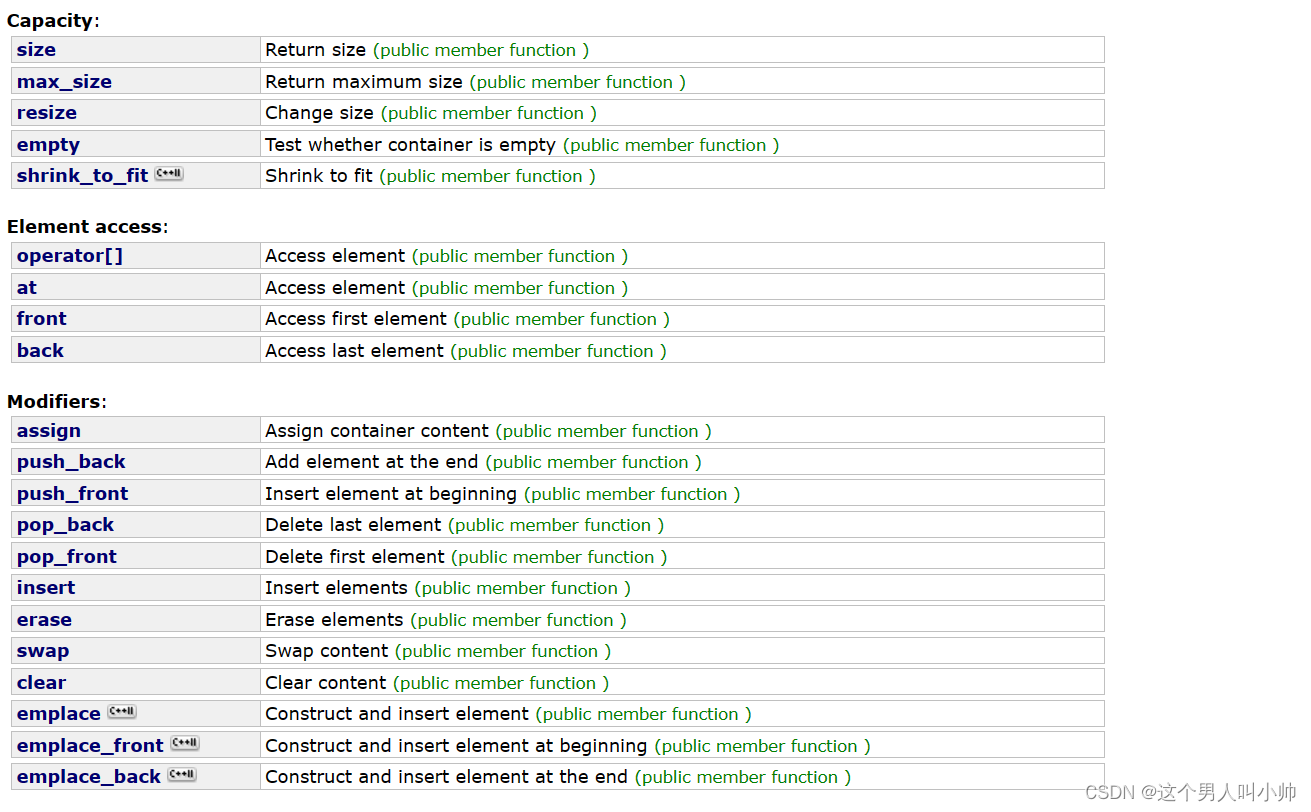
3. stack基础容器可以是任何标准容器类模板，也可以是一些其他专门设计的容器类。容器应支持以下操作：

empty
size
back
push_back
pop_back

4. 标准容器类，并满足这些要求。默认情况下，如果未为特定类实例化指定容器类，则使用标准容器。vectordequeliststackdeque

包括queue，它们都是适配器，它们没有使用数组或链表单独实现它们的功能，它们是依靠封装的容器，将数据存在封装的容器内，然后根据要求适配出相应的需求。

作为容器适配器的stack，它没有迭代器，因为stack的特性，不能支持迭代器的随便访问

适配器的本质是一种复用，是一种设计模式

一、stack的使用

1. 接口说明

函数说明	接口说明
stack()	构造空的栈
empty()	检查stack是否为空
size()	返回stack中元素的个数
top()	返回栈顶元素的引用
push()	将元素val压入stack中
pop()	将stack中尾部的元素弹出

相应的接口十分易懂，我们简单看例子即可

	std::stack<int> st;
	st.push(1);
	st.push(2);
	st.push(3);
	st.push(4);

	while (!st.empty())
	{
		cout << st.top() << " ";
		st.pop();
	}

2. 例题

例1：155. 最小栈

如果只是增加一个min成员变量是有bug的，当最小值出栈后，min不会更新
创建两个栈，栈1正常存数据，栈2存最小值，当栈1数据出栈时，判断其与栈2栈顶数据是否相等，若相等，则栈1、2都出栈一次；当栈1数据压栈时，判断其与栈2的栈顶数据是否相等，若相等则栈2也压栈相同数据，这是为了防止栈1有多个相同的最小值，栈1出栈最小数据后，栈2对应的最小值没有了，这就会出现问题
//用两个栈，一个栈存正常的数据，另一个栈存最小值
class MinStack {
public:
    MinStack() //初始化列表，默认调用自定义类型的构造函数
    {}
    
    void push(int val) {
        _st.push(val);
        if (min_st.empty() || val <= min_st.top())
        {
            min_st.push(val);
        }
    }
    
    void pop() {

        if (_st.top() == min_st.top())
        {
            min_st.pop();
        }

        _st.pop();
    }
    
    int top() {
        return _st.top();
    }
    
    int getMin() {
        return min_st.top();
    }

private:
    stack<int> _st;
    stack<int> min_st;
};

例2. JZ31 栈的压入、弹出序列

模拟出栈，每次匹配，不同，则入栈，相同则出栈

class Solution {
public:

    bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
        stack<int> st;
        int pushi = 0, popi = 0;    //pushi控制pushV下标，popi控制popV下标
        while (pushi < pushV.size())
        {
            st.push(pushV[pushi++]);
            if (st.top() != popV[popi])
            {
                continue;
            }
            else 
            {
                //相等则出栈
                while (!st.empty() && st.top() == popV[popi])
                {
                    st.pop();
                    ++popi;
                }
            }
        }

        return st.empty();
    }
};

逻辑优化

class Solution {
public:
    bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
        stack<int> st;
        int pushi = 0, popi = 0;
        while (pushi < pushV.size())
        {
            st.push(pushV[pushi++]);
            while (!st.empty() && st.top() == popV[popi])
            {
                st.pop();
                ++popi;
            }
        }

        return st.empty();
    }
};

例3. 150. 逆波兰表达式求值

创建一个栈，遍历vector
如果是数字就压栈，使用 stoi 接口
如果是操作符就出栈两次，先出栈的为右操作数，后出栈的为左操作数，计算后再将结果压栈

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        stack<int> st;
        for (auto& str : tokens)
        {
            if (str == "+" || str == "-" || str == "*" || str == "/")
            {
                int right = st.top();
                st.pop();
                int left = st.top();
                st.pop();
                switch(str[0])
                {
                    case '+':
                        st.push(left + right);
                        break;
                    case '-':
                        st.push(left - right);
                        break;
                    case '*':
                        st.push(left * right);
                        break;
                    case '/':
                        st.push(left / right);
                        break;
                }
            }
            else
                st.push(stoi(str));
        }

        return st.top();
    }
};

补充：如何将中序表达式改为后序表达式？

开辟两个栈，遍历表达式
对于操作数直接入栈1
对于操作符，若栈2不为空或当前操作符比栈顶的优先级高，继续入栈；若栈不为空且当前操作符比栈顶的优先级低或相等，则将栈顶操作符压栈栈1
表达式结束后，依次出栈2里面的操作符

类比：

类比stack容器，我们来看看queue例题

102. 二叉树的层序遍历

思路：

我们可以用一种巧妙的方法修改广度优先搜索：

        1. 首先根元素入队
        2. 当队列不为空的时候
2.1 求当前队列的长度 i

2.2 依次从队列中取 i 个元素进行拓展，然后进入下一次迭代
        它和普通广度优先搜索的区别在于，普通广度优先搜索每次只取一个元素拓展，而这里每次取 i 个元素。在上述过程中的第 i 次迭代就得到了二叉树的第 i 层的i个元素。
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) 
    {
        vector<vector<int>> ret;    //存结果
        queue<TreeNode*> q;        //存各节点
        if (!root)
            return ret;
        //入队根节点
        q.push(root);

        while(!q.empty())
        {
            //当前队列存在的数据个数就是该层的数据的个数
            int currentLeveSize = q.size();
            ret.push_back(vector<int> ());
            //当前层的所有结点的所有孩子结点，就是下一层的数据个数
            for (int i = 0; i < currentLeveSize; i ++ )
            {
                auto node = q.front();
                q.pop();
                ret.back().push_back(node->val);
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
        }
        
       return ret;
    }
};

二、模拟实现stack

.h文件不编译，只展开，如果在
#include "Stack.h"
之前，写了各种头文件，并且展开了命名空间std，那么程序是可以运行的，.h文件里需要使用的函数都已经在上面展开

如果将
#include "Stack.h"
using namespace std;
.h文件写在std之前，那么.h文件里如果使用std里的内容，编译器会报错，这是因为，编译器只会向上查找，为std是在.h文件下面展开的，所以.h文件是找不到std围起的内容

所以，.h文件和std展开的位置是很重要的。

我们知道，stack是适配器模式，我们之前写的数据结构只能选择顺序存储或链式存储，并不能相互转换，而适配器模式可以使用模板来随时转换储存结构，这就是大佬实现STL的stack的高处所在。
stack<int, vector<int>> st1;
stack<int, list<int>> st2;

容器适配器：对容器进行封装，适配出我们想要的

对于适配器的栈，不需要构造函数、析构函数，因为它的成员变量是一个自定义类型的容器，自动调用其构造函数、析构函数.

Container使用缺省模板

#pragma once
#include<iostream>
#include<deque>
using namespace std;

namespace my_stack
{
	//容器适配器，对容器进行封装，适配出我们想要的
	template<class T, class Container = deque<T>>
	class stack
	{
	public:
		void push(const T& x)
		{
			_con.push_back(x);
		}

		void pop()
		{
			_con.pop_back();
		}

		T& top()
		{
			//不能用[]，因为可能是链表
			return _con.back();
		}

		size_t size()
		{
			return _con.size();
		}

		bool empty()
		{
			return _con.empty();
		}

	private:
		Container _con;
	};
}

三、queue的使用

FIFO queue

1. 队列是一种容器适配器，专门用于在 FIFO 上下文 ( 先进先出 )中操作，其中从容器一端插入元素，另一端提取元素。

2. 队列作为容器适配器实现，容器适配器即将特定容器类封装作为其底层容器类， queue 提供一组特定的成员函数来访问其元素。元素从队尾入队列，从队头出队列。

3. 底层容器可以是标准容器类模板之一，也可以是其他专门设计的容器类。该底层容器应至少支持以下操作:

        empty：检测队列是否为空

        size：返回队列中有效元素的个数

        front：返回队头元素的引用

        back：返回队尾元素的引用

        push_back：在队列尾部入队列

        pop_front：在队列头部出队列

4. 标准容器类 deque 和 list 满足了这些要求。默认情况下，如果没有为 queue 实例化指定容器类，则使用标准容器deque 。

函数说明	接口说明
queue()	构造空的队列
empty()	检测队列是否为空
size()	返回队列中有效元素的个数
front()	返回队头元素的引用
back()	返回队尾元素的引用
push()	在队尾将元素val入队列
pop()	将队头元素出队列

使用方法同stack

四、模拟实现queue

对于queue来说，STL实现时，就按照了链表容器来实现，不能使用vector容器，因为在pop时，queue调用的是pop_front()函数，而vector没有该函数

为什么不适配vector呢？

问题也显而易见，vector的pop_front效率太低了

#pragma once
#include<iostream>
#include<deque>
using namespace std;

namespace my_queue
{
	//容器适配器，对容器进行封装
	template<class T, class Container = deque<T>>
	class queue
	{
	public:
		void push(const T& x)
		{
			_con.push_back(x);
		}

		void pop()
		{
			_con.pop_front();
		}

		T& front()
		{
			//不能用[]，因为可能是链表
			return _con.front();
		}

		T& back()
		{
			//不能用[]，因为可能是链表
			return _con.back();
		}

		size_t size()
		{
			return _con.size();
		}

		bool empty()
		{
			return _con.empty();
		}

	private:
		Container _con;
	};
}

五、deque

双端队列

Deque（通常发音为“deck”）是 double-ended queue 的不规则首字母缩写。双端队列是具有动态大小的序列容器，可以在两端（其前端或后端）扩展或收缩。

特定的库可以以不同的方式实现 deque，通常作为某种形式的动态数组。但无论如何，它们都允许通过随机访问迭代器直接访问单个元素，并根据需要通过扩展和收缩容器来自动处理存储。

因此，它们提供了类似于vector的功能，但在序列的开头，而不仅仅是在序列的末尾，都可以有效地插入和删除元素。但是，与vector不同的是，deques 不能保证将其所有元素存储在连续的存储位置：通过偏移指向另一个元素的指针来访问 a 中的元素会导致未定义的行为。

vector 和 deque 都提供了非常相似的接口，可以用于类似的目的，但在内部，它们的工作方式完全不同：虽然vector使用单个数组，需要偶尔重新分配以进行增长，但 deque 的元素可以分散在不同的存储块中，容器在内部保留必要的信息，以提供对其任何元素的直接访问，时间恒定且均匀顺序接口（通过迭代器）。因此，deques 在内部比 vector 复杂一些，但这允许它们在某些情况下更有效地增长，尤其是在非常长的序列中，重新分配变得更加昂贵。

对于涉及在开头或结尾以外的位置频繁插入或删除元素的操作，deques 的性能较差，并且迭代器和引用的一致性低于列表和转发列表。

可以看出，双端队列deque表现十分出色，堪称“六边形战士”，但是如此出色的容器，为什么出名度不及vector、string呢？这是因为deque对于涉及在开头或结尾以外的位置频繁插入或删除元素的操作，deques 的性能较差，什么都可以，但什么都不精通。

相比vector：

相比list：

deque缺陷：

1. 不适合随机访问

2. 不适合高频访问

3. 不适合中间位置插入删除

所以这个容易并不常用。

所以deque相比vector、list更适合作为stack、queue的容器，stack、queue不会在中间位置插入删除，是高频的头尾操作。