一
了解一些散列的基本概念,仅从文字角度,整理了最基础的定义。
发现一本书,《算法图解》,微信读书APP可读,有图,并且是科普性质的读物,用的比喻很生活化,可以与《算法导论》合并起来看,会轻松很多。
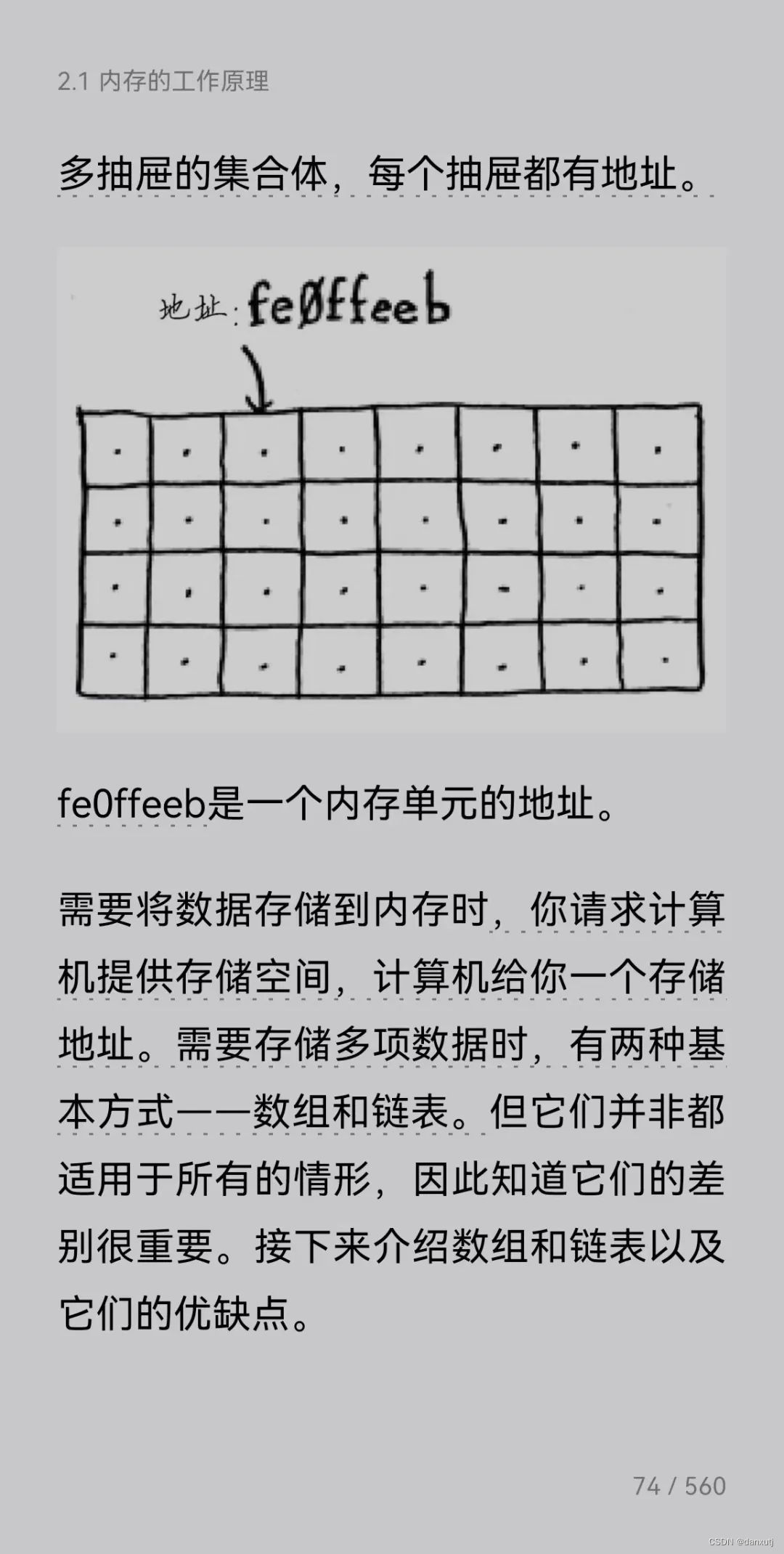
P142散列数 hash table 槽 slot 对应全域中一个关键字
两个关键字映射到同一个槽里:冲突
散列,本质就是把任意长度的输入通过散列算法变成固定长度的输入,你可以理解为它是一种压缩性的映射,所以散列值的空间会小于输入空间,便于储存。
又因为它很难找到逆向规律的特性,所以也可以用作数字签名来保障数据传递的安全性,散列也称为哈希(Hash),hash算法也因此被广泛应用在互联网应用中。
散列表的基本概念
假设某应用要用到一个动态集合,其中每个元素都有一个属于[0…p]的关键字,此处p是一个不太大的数,且没有两个元素具有相同的关键字,则可以用一个数组[p+1]存储该动态集合,并且使用关键字作为数组下标进行直接寻址。这一直接寻址思想在前面的非比较排序中就有所应用。然而,当p很大并且实际要存储的动态集合大小n<<p时,这样一个数组将浪费大部分空间。< p=“”></p时,这样一个数组将浪费大部分空间。<>
散列表(Hash table),使用具有m个槽位的数组来存储大小为n的动态集合。α=n/m被定义为散列表的装载因子。在散列表中,具有关键字k的元素的下标为h(k),即利用散列函数h,根据关键字k计算出槽的位置。散列函数h将关键字域[0…p]映射到散列表[0…m-1]的槽位上,这里,m可以远小于p,从而缩小了需要处理的下标范围,并相应地降低了空间开销。散列表带来的问题是:两个关键字可能映射到同一个槽上,这种情形称为碰撞。因此,散列函数h应当将每个关键字等可能地散列到m个槽位的任何一个中去,并与其它关键字已被散列到哪一个槽位中无关,从而避免或者至少最小化碰撞
二
散列冲突解决方案
- 开放寻址法
开放寻址法的核心思想是,如果出现了散列冲突,我们就重新探测一个空闲的位置。
开放寻址法解决方案有线性探测法、二次探测、双重散列等方案:
线性探测法(Linear Probing):1)插入数据:当我们往散列表中插入数据时,如果某个数据经过散列函数之后,存储的位置已经被占用了,我们就从当前位置开始,依次往后查找(到底后从头开始),看是否有空闲位置,直到找到为止。
2)查找数据:我们通过散列函数求出要查找元素的键值对应的散列值,然后比较数组中下标为散列值的元素和要查找的元素是否相等,若相等,则说明就是我们要查找的元素;否则,就顺序往后依次查找。如果遍历到数组的空闲位置还未找到,就说明要查找的元素并没有在散列表中。
当然这里存在一个问题,就是存数据那块位置往前的某个数据被删除了,那么线性探索查到那块位置的时候就会判断元素不在散列表,查找就会失效,面对这个问题,我们在删除的时候,用下面删除的方法
P156完全散列 perfect hashing 关键字集合是静态 像CD-ROM一样存入不可变 马尔可夫不等式 摊还期望时间
全域散列,它在任意输入的情况下都能达到比较好的平均情况性能。但值得注意的是“平均情况性能”这六个字,就像BFPRT——Top k问题的终极解法一文中介绍的随机快速选择算法一样,虽然很难遇到导致最坏情况发生的输入,但这种可能性仍然是存在的,没有完全消除。我们需要继续追寻,找到像BFPRT一样,能在确定情况下提供出色的最坏情况性能的散列算法。
完全散列算法给出了关键字集合为静态时的解决方案。我们来看看它如何在最坏情况下达到 O(1) 的时间复杂度。最直接的想法,让散列数组的长度 m 尽量大,因为对于固定的关键字集合, m 越大,冲突的可能性就越低。但是,无论 m 取多大的数,冲突的可能性都不会降到0,只会越来越接近0。此时,静态关键字集合的好处就出来了,当冲突的可能性较低时,我们可以多试几个散列函数,找到不发生冲突的那个,确定为最终使用的散列函数。
三
FPGA与散列数相关的应用举例:
安全散列算法SHA(Secure Hash Algorithm,SHA)是美国国家标准和技术局发布的国家标准FIPS PUB 180-1,般称为SHA-1。其可对长度不超过264位的消息产生160位的消息摘要输出,可在NIST的网站上获得该算法的数学原理。IFF(Identification Friend or Foe, IFF)用于确定输入密钥是否正确。
其工作方式如下:
①在FPGA内部构造随机数生成模块,用于产生消息Q,并通过1-Wire总线发送DS2432芯片
②DS2432内部拥有一个由设计者设定的密钥。由该密钥并结合
③与此同时,FPGA内部产生一个期望的响应E,判断该期望响应是否与DS2432的真实响应A一致
④如果E与A吻合,则判断该设计为正版设计;否则判定为盗版设计;
⑤最终,FPGA程序可以对盗版设计做出程序锁止或减少功能。

![[C国演义] 第十八章](https://img-blog.csdnimg.cn/f091e69923d44ee09c05cab21b4d37e5.png)