[C国演义] 第十八章

news2025/1/10 23:58:58

第十八章

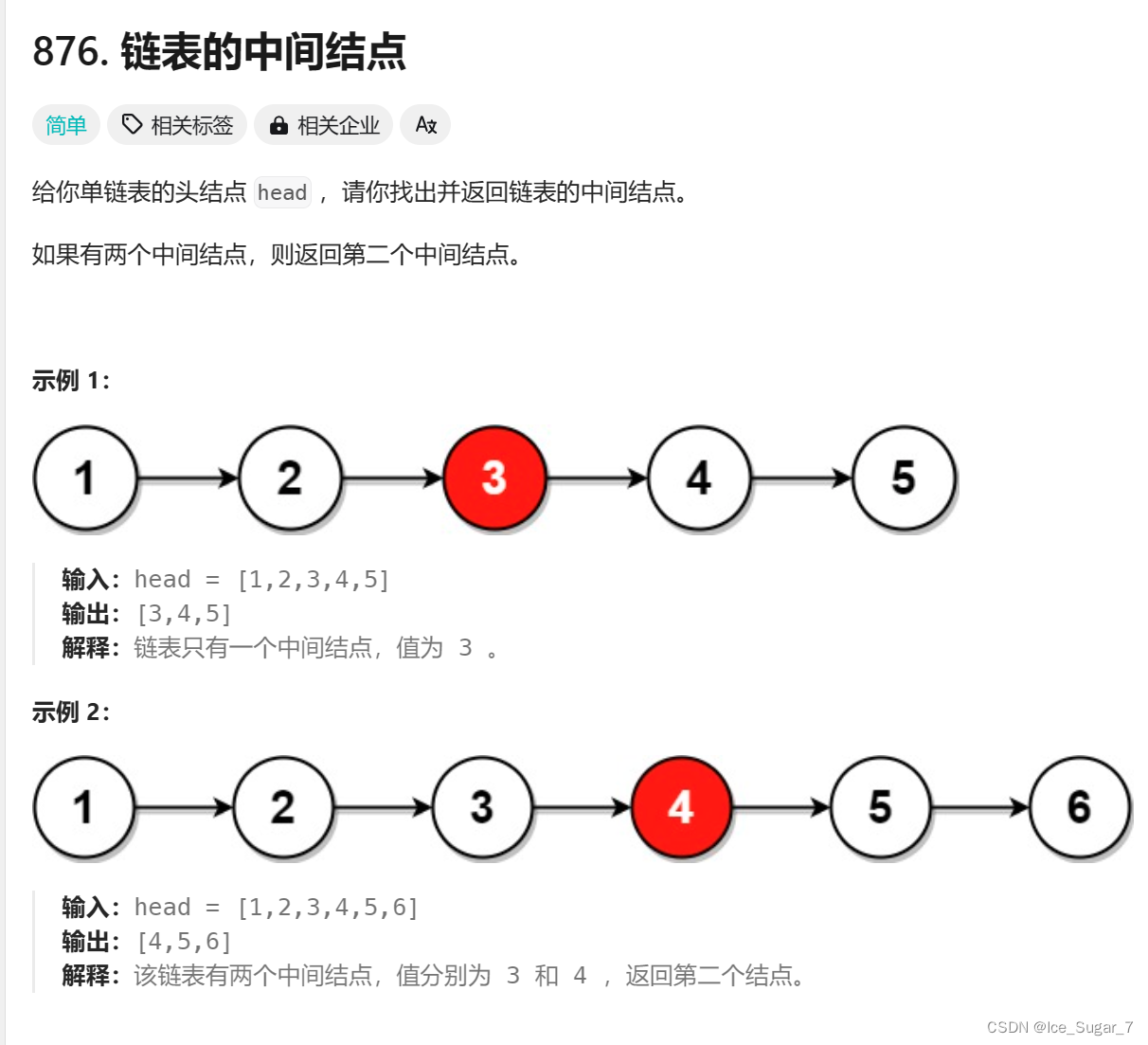
最长斐波那契子序列的长度
最长等差数列
等差序列划分II - 子序列

最长斐波那契子序列的长度

力扣链接

子序列 ⇒ dp[i] — — 以 arr[i] 结尾的所有子序列中, 斐波那契子序列的最长长度
子序列 ⇒ 状态转移方程 — — 根据最后一个位置的组成来划分
初始化 — — 根据状态转移方程, 全都初始化为 2
遍历顺序 — — 根据状态转移方程, 从前往后
返回结果 — — 返回dp表中的最大值, 记作res; 如果res < 3, 那就返回0, 如果res > 3, 那就返回res

class Solution {
public:
    int lenLongestFibSubseq(vector<int>& arr) 
    {
        int n = arr.size();

        // 建表 + 初始化
        vector<vector<int>> dp(n, vector<int>(n, 2));

        // 记录返回结果
        int res = 2;

        // 优化
        unordered_map<int, int> hash; // <数组元素, 下标>
        for(int i = 0; i < n; i++)
        {
            hash[arr[i]] = i;
        }

        // 填表
        for(int j = 2; j < n; j++) // 最后一个元素
        {
            for(int i = 1; i < j; i++) // 倒数第二个元素
            {

                int target = arr[j] - arr[i]; // 第一个元素
                // 斐波那契数列 -- 递增的
                if(target < arr[i] && hash.count(target))
                {
                    dp[i][j] = dp[hash[target]][i] + 1;
                }

                res = max(res, dp[i][j]);
            }
        }

        // 返回结果
        return res < 3 ? 0 : res;
    }
};

最长等差数列

力扣链接
在这里插入图片描述

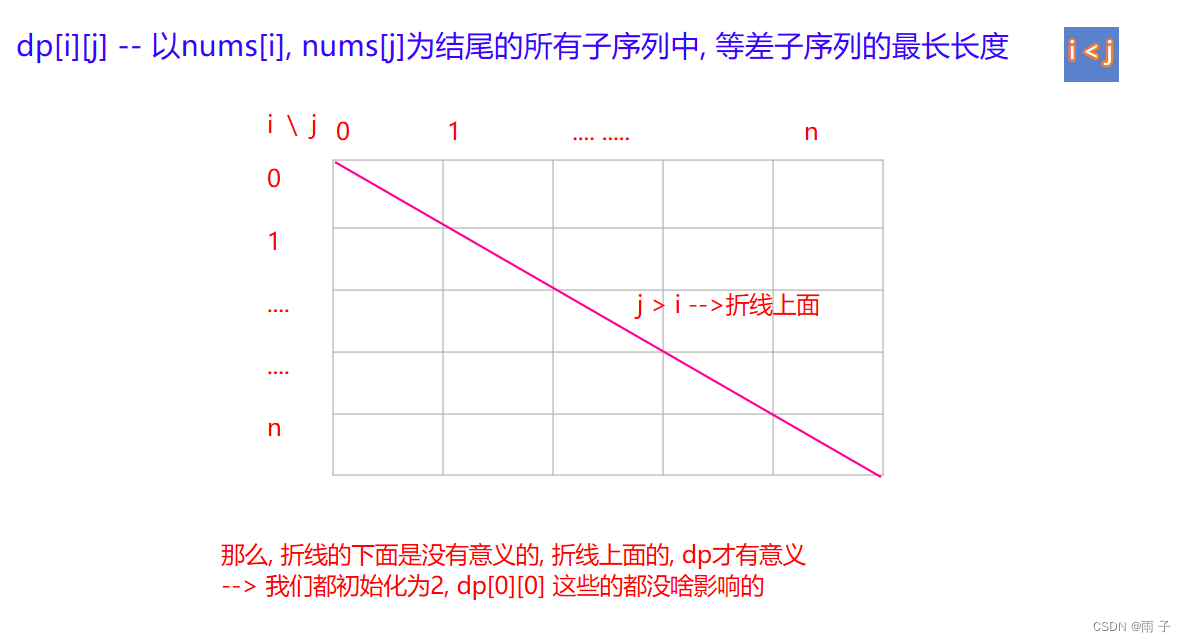
子序列 ⇒ dp[i]的含义: dp[i]的含义: 以nums[i] 为结尾的所有子序列中, 等差子序列的最长长度
子序列 ⇒ 状态转移方程 :
初识化 : 都初始化为 2
🗨️dp[0][0] 也初始化为 2?
遍历顺序 : 根据 优化, 我们采取 固定第二个元素, 再枚举最后一个元素的遍历顺序
返回结果 : 返回dp表中的最大值

class Solution {
public:
    int longestArithSeqLength(vector<int>& nums) 
    {
        int n = nums.size();

        // 建表 + 初始化
        vector<vector<int>> dp(n, vector<int>(n, 2));

        // 优化
        unordered_map<int, int> hash; // <数组元素, 下标>
        hash[nums[0]] = 0;

        int res = 2;
        // 先固定倒数第二个元素,在枚举最后一个元素 && 边dp边插入hash
        // -- 有利于找到离i最近的一个target
        for(int i = 1; i < n; i++) // 先固定倒数第二个元素
        {
            for(int j = i + 1; j < n; j++) // 枚举最后一个元素
            {
                int target = 2 * nums[i] - nums[j]; // 目标的第一个元素
                if(hash.count(target)) // 如果存在, 更新dp[i][j]
                {
                    dp[i][j] = dp[hash[target]][i] + 1;
                }

                res = max(res, dp[i][j]);
            }

            // 依次插入hash表中
            hash[nums[i]] = i;
        }

        return res;
    }
};

等差序列划分II - 子序列

力扣链接
在这里插入图片描述

子序列 ⇒ dp[i] : 以nums[i] 为结尾的所有子序列中, 等差子序列的最大数目
子序列 ⇒ 状态转移方程 : 根据最后一个位置划分
初始化 : 全都初始化为 0
遍历顺序 : 根据优化 ⇒ 先固定倒数第二个元素, 再枚举最后一个元素
返回结果 : 累加dp表

class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& nums) 
    {
        int n = nums.size();

        // 建表 + 初始化
        vector<vector<int>> dp(n, vector<int>(n, 0));

        // 优化
        // 由于前面存在多个target && 我们要全部累加起来
        // --> 所以, 用一个vector来接收一下下标
        unordered_map<long long int, vector<int>> hash; // <数组元素, 下标>
        hash[nums[0]].push_back(0);

        int res = 0;

        // 先固定倒数第二个元素,在枚举最后一个元素 && 边dp边插入hash
        for(int i = 1; i < n; i++) // 先固定倒数第二个元素
        {
            for(int j = i + 1; j < n; j++) // 枚举最后一个元素
            {
                long long int target = (long long int ) 2 * nums[i] - nums[j]; // 目标的第一个元素
                if(hash.count(target)) // 如果存在, 更新dp[i][j]
                {
                    // 这里的 k 都是在合理区间内的, 全部累加
                    for(auto k : hash[target])
                    {
                        // 全部都累加起来
                        dp[i][j] += dp[k][i] + 1;
                    }
                }

                res += dp[i][j];
            }

            // 依次插入hash表中
            hash[nums[i]].push_back(i);
        }

        return res;
    }
};