目录
1、【二分】
(1)r=mid —— 大于等于某数的最小值
(2)l=mid —— 小于等于某数的最大值
2、【前缀和】
(1)一维前缀和
(2)二维前缀和
3、【差分】
(1)一维差分
(2)二维差分
4、【单调栈】
(1)单调递增栈
(2)单调递减栈
5、【并查集】
6、【BFS 求最短路】
为什么BFS可以求最短路?
7、【Dijkstra】
8、【spfa】
9、【floyd】
10、【kruskal】
11、【质数】
12、【约数】
1、【二分】
【蓝桥杯集训3】二分专题(3 / 5)-CSDN博客
- l + r >> 1 —— 先 r = mid 后 l = mid+1 —— 寻找左边界 —— 找大于等于某数的最小值
- l+r+1>>1 —— 先 l = mid 后 r = mid-1 —— 寻找右边界 —— 找小于等于某数的最大值
(1)r=mid —— 大于等于某数的最小值
1 2 3 3 3 3 4 5
int l=0,r=n-1;
while(l<r)
{
int mid=l+r>>1;
if(a[mid]>=x) r=mid;
else l=mid+1;
}(2)l=mid —— 小于等于某数的最大值
1 2 3 3 3 3 4 5
int l=0,r=n-1;
{
int mid=l+r+1>>1;
if(a[mid]<=x) l=mid;
else r=mid-1;
}2、【前缀和】
【蓝桥杯集训1】前缀和专题(4 / 5)-CSDN博客
(1)一维前缀和
a数组下标从1开始,Si = Si-1 + ai
则 [ Al,Ar ]段的和 = s[r] - s[l-1]
for(int i=1;i<=n;i++)
{
a[i]=sc.nextInt();
s[i]=s[i-1]+a[i];
}
[Al,Ar]的和 = s[r]-s[l-1]
(2)二维前缀和

static int N=1010; static int[][] a=new int[N][N],s=new int[N][N]; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { a[i][j]=sc.nextInt(); s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j]; }
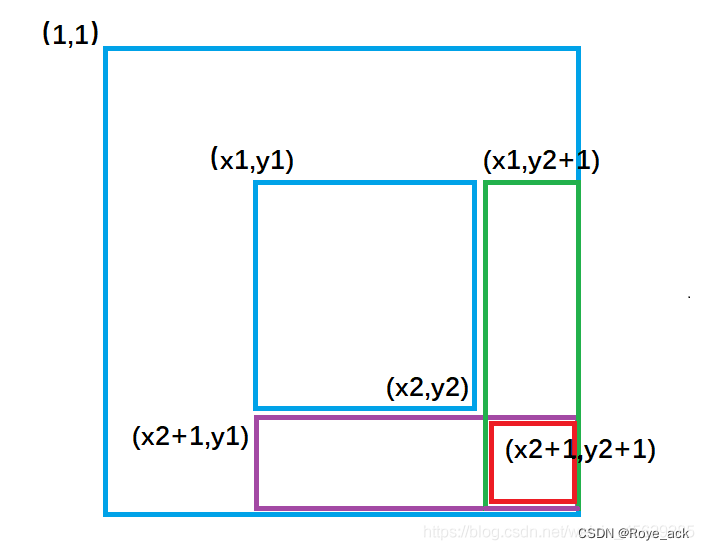
while(q-->0) { int x1=sc.nextInt(),y1=sc.nextInt(),x2=sc.nextInt(),y2=sc.nextInt(); int res=s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]; System.out.println(res); }
3、【差分】
【蓝桥杯集训2】差分专题(3 / 4)-CSDN博客
(1)一维差分
给a数组 [l,r] 区间的每个数+c,只需要给其差分数组b做如下操作即可
b[l]+=c; b[r+1]-=c;
构造差分数组
int[] a=new int[N]; int[] b=new int[N]; for(int i=1;i<=n;i++) { a[i]=sc.nextInt(); b[i]=a[i]-a[i-1]; //构造差分数组 }差分数组进行
![\large b\left [ l \right ]+=c](https://latex.csdn.net/eq?%5Clarge%20b%5Cleft%20%5B%20l%20%5Cright%20%5D+%3Dc)
操作
int l,r,c; while(k-->0) { b[l]+=c; b[r+1]-=c; }最后求差分数组b的前缀和即为原数组在【l,r】段+c的数组
for(int i=1;i<=n;i++) { a[i]=a[i-1]+b[i]; //b的前缀和是a System.out.print(a[i]+" "); }
(2)二维差分
初始化
static int N=1010; static int[][] a=new int[N][N],b=new int[N][N]; public static void work(int x1,int y1,int x2,int y2,int c) { b[x1][y1]+=c; b[x2+1][y1]-=c; b[x1][y2+1]-=c; b[x2+1][y2+1]+=c; } for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { a[i][j]=sc.nextInt(); work(i,j,i,j,a[i][j]); }求前缀和
work(x1,y1,x2,y2,c); for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1]; System.out.print(b[i][j]+" "); } System.out.println(); }
4、【单调栈】
【蓝桥杯集训9】单调栈、单调队列(模拟栈、模拟队列)专题(3 / 3)_Roye_ack的博客-CSDN博客
(1)单调递增栈
- 在保持栈内元素单调递增前提下(如果栈顶元素大于待入栈元素,弹出栈顶),新元素入栈
- 对于要入栈的元素,在对栈进行更新后,栈顶元素就是数组中左侧第一个比自己小的元素
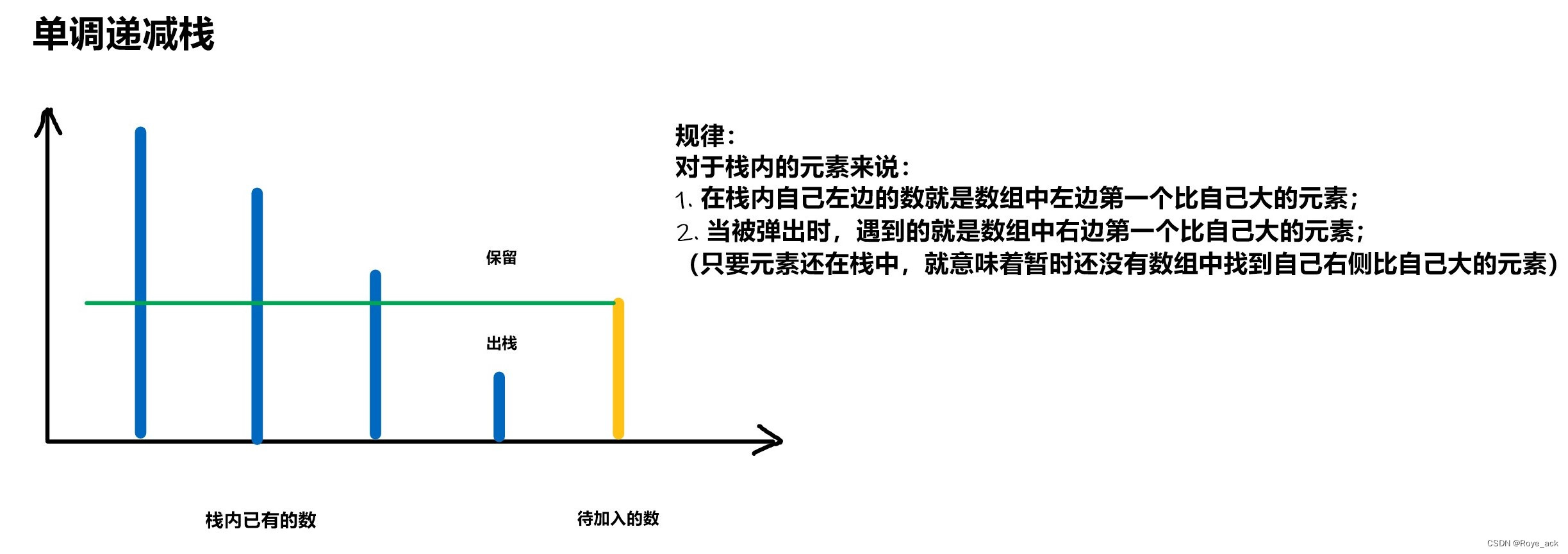
(2)单调递减栈
- 在保持栈内元素单调递减前提下(如果栈顶元素小于要待入栈元素,弹出栈顶),新元素入栈
- 对于要入栈的元素,在对栈进行更新后,栈顶元素就是数组中左侧第一个比自己大的元素
题目:输出每个数左边第一个比自己小的数,如果不存在则输出-1
class Main
{
public static void main(String[] args)
{
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
Deque<Integer> stk=new LinkedList<>();
while(n-->0)
{
int x=sc.nextInt();
while(!stk.isEmpty()&&stk.peek()>=x) stk.pop();
if(stk.isEmpty()) System.out.print("-1 ");
else System.out.print(stk.peek()+" ");
stk.push(x);
}
}
}
5、【并查集】
【蓝桥杯集训7】并查集专题(3 / 5)-CSDN博客
int find(int x) //返回x的祖宗结点+状态压缩 { if(p[x]!=x) p[x]=find(p[x]); return p[x]; } p[find(a)]=find(b); //合并操作 给a认个祖宗b if(find(a)==find(b)) //a和b元素在同一个集合 for(int i=1;i<=n;i++) p[i]=i;
import java.util.*;
class Main
{
static int N=100010;
static int[] p=new int[N];
public static int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]); //如果不是祖宗,则向上查找
return p[x];
}
public static void unite(int a,int b)
{
p[find(a)]=find(b); //给a认个祖宗b
}
public static void main(String[] args)
{
Scanner sc=new Scanner(System.in);
int n=sc.nextInt(),m=sc.nextInt();
for(int i=1;i<=n;i++) p[i]=i;
while(m-->0)
{
String s=sc.next();
int a=sc.nextInt(),b=sc.nextInt();
if(s.equals("M"))
{
if(find(a)!=find(b)) unite(a,b);
}
else
{
if(find(a)==find(b)) System.out.println("Yes");
else System.out.println("No");
}
}
}
}
6、【BFS 求最短路】
【蓝桥杯集训11】BFS(4 / 4)_Roye_ack的博客-CSDN博客
为什么BFS可以求最短路?
为什么就算有多条通路,它总能输出最小距离?
因为当第一个点到达终点时,它一定是最短距离,并且会将终点标记,那么其他点再也无法到达终点,也更新不了初始点到终点的距离将起点(0,0)入队,上下左右走,只要在合法的范围内且不碰到墙且没有走过,则入队
BFS就是将所有能走的路都走,第一条能走通的路一定是最短路
static int[][] g=new int[110][110];
static int[][] d=new int[110][110]; //记录该点到起点的最短距离
static int[][] st=new int[110][110]; //标记走过的点
static int[] dx={-1,1,0,0};
static int[] dy={0,0,-1,1}; //方向数组 public static int bfs()
{
d[0][0]=0;
Queue<PII> q=new LinkedList<>();
q.offer(new PII(0,0));
while(!q.isEmpty())
{
PII t=q.poll();
for(int i=0;i<4;i++)
{
int nx=t.x+dx[i];
int ny=t.y+dy[i];
if(nx>=0&&nx<n&&ny>=0&&ny<m&&g[nx][ny]==0&&st[nx][ny]==0)
{
q.offer(new PII(nx,ny));
d[nx][ny]=d[t.x][t.y]+1;
st[nx][ny]=1;
}
}
}
return d[n-1][m-1];
}