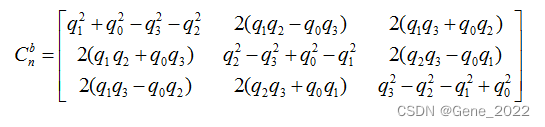上两节,我们依次讲了树、二叉树、二叉查找树。二叉查找树是最常用的一种二叉树,它支持快速插入、删除、查找操作,各个操作的时间复杂度跟树的高度成正比,理想情况下,时间复杂度是O(logn)。
不过,二叉查找树在频繁的动态更新过程中,可能会出现树的高度远大于log2n的情况,从而导致各个操作的效率下降。极端情况下,二叉树会退化为链表,时间复杂度会退化到O(n)。我上一节说了,要解决这个复杂度退化的问题,我们需要设计一种平衡二叉查找树,也就是今天要讲的这种数据结构。
很多书籍里,但凡讲到平衡二叉查找树,就会拿红黑树作为例子。不仅如此,如果你有一定的开发经验,你会发现,在工程中,很多用到平衡二叉查找树的地方都会用红黑树。你有没有想过,为什么工程中都喜欢用红黑树,而不是其他平衡二叉查找树呢?
带着这个问题,让我们一起来学习今天的内容吧!
什么是“平衡二叉查找树”?
平衡二叉树的严格定义是这样的:二叉树中任意一个节点的左右子树的高度相差不能大于1。从这个定义来看,上一节我们讲的完全二叉树、满二叉树其实都是平衡二叉树,但是非完全二叉树也有可能是平衡二叉树。
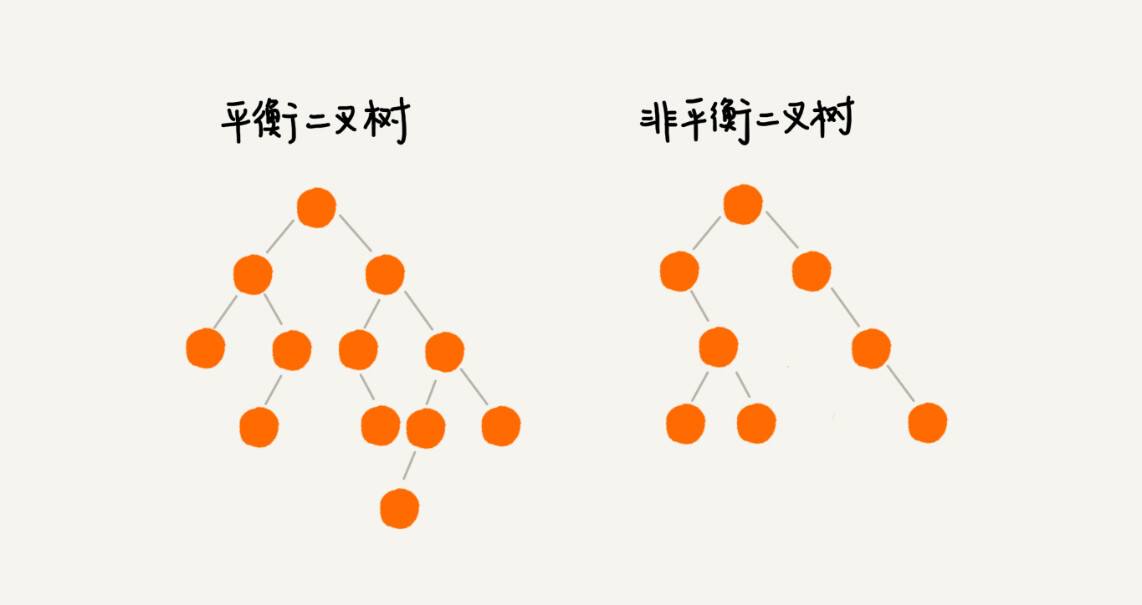
平衡二叉查找树不仅满足上面平衡二叉树的定义,还满足二叉查找树的特点。最先被发明的平衡二叉查找树是AV