目录
- 1. 梯度下降法
- 1.1 一元线性回归
- 1.2 多元线性回归
- 1.3 标准方程法
- 1.4 梯度下降法与标准方程法的优缺点
- 2. 相关系数与决定系数
1. 梯度下降法
1.1 一元线性回归
定义一元线性方程
y
=
ω
x
+
b
y=\omega x+b
y=ωx+b
则误差(残差)平方和
C
(
ω
,
b
)
=
∑
i
=
1
n
(
y
i
^
−
y
i
)
2
C(\omega,b)=\sum_{i=1}^n(\hat{y_i}-y_i)^2
C(ω,b)=i=1∑n(yi^−yi)2
即
C
(
ω
,
b
)
=
∑
i
=
1
n
(
ω
x
i
+
b
−
y
i
)
2
C(\omega,b)=\sum_{i=1}^n(\omega x_i+b-y_i)^2
C(ω,b)=i=1∑n(ωxi+b−yi)2
为方便计算,常写为如下形式
C
(
ω
,
b
)
=
1
2
n
∑
i
=
1
n
(
ω
x
i
+
b
−
y
i
)
2
C(\omega,b)=\frac{1}{2n}\sum_{i=1}^n(\omega x_i+b-y_i)^2
C(ω,b)=2n1i=1∑n(ωxi+b−yi)2
其中,
y
i
y_i
yi为真实值,
y
i
^
\hat{y_i}
yi^为预测值。
若用一元线性方程拟合上面的数据集,那么最佳的拟合直线方程需满足
C
(
ω
,
b
)
C(\omega,b)
C(ω,b)最小,即使得真实值到直线竖直距离的平方和最小。因此需要求解使得
C
(
ω
,
b
)
C(\omega,b)
C(ω,b)最小的参数
ω
\omega
ω和
b
b
b,即
min
ω
,
b
C
(
ω
,
b
)
\min_{\omega,b}C(\omega,b)
ω,bminC(ω,b)
梯度下降公式
ω
:
=
ω
−
α
∂
C
(
ω
,
b
)
∂
ω
=
ω
−
α
1
n
∑
i
=
1
n
(
ω
x
i
+
b
−
y
i
)
2
x
i
\omega:=\omega-\alpha \frac{\partial C(\omega,b)}{\partial \omega}=\omega-\alpha \frac{1}{n}\sum_{i=1}^n(\omega x_i+b-y_i)^2x_i
ω:=ω−α∂ω∂C(ω,b)=ω−αn1i=1∑n(ωxi+b−yi)2xi
b
:
=
b
−
α
∂
C
(
ω
,
b
)
∂
b
=
b
−
α
1
n
∑
i
=
1
n
(
ω
x
i
+
b
−
y
i
)
2
b:=b-\alpha \frac{\partial C(\omega,b)}{\partial b}=b-\alpha \frac{1}{n}\sum_{i=1}^n(\omega x_i+b-y_i)^2
b:=b−α∂b∂C(ω,b)=b−αn1i=1∑n(ωxi+b−yi)2
其中
α
\alpha
α为步长(学习率),
:
=
:=
:=表示赋值操作。
梯度下降基本步骤
- 初始化 ω \omega ω和 b b b(常取0)
- 不断改变 ω \omega ω和 b b b,直到 C ( ω , b ) C(\omega,b) C(ω,b)到达一个全局最小值,或局部极小值。
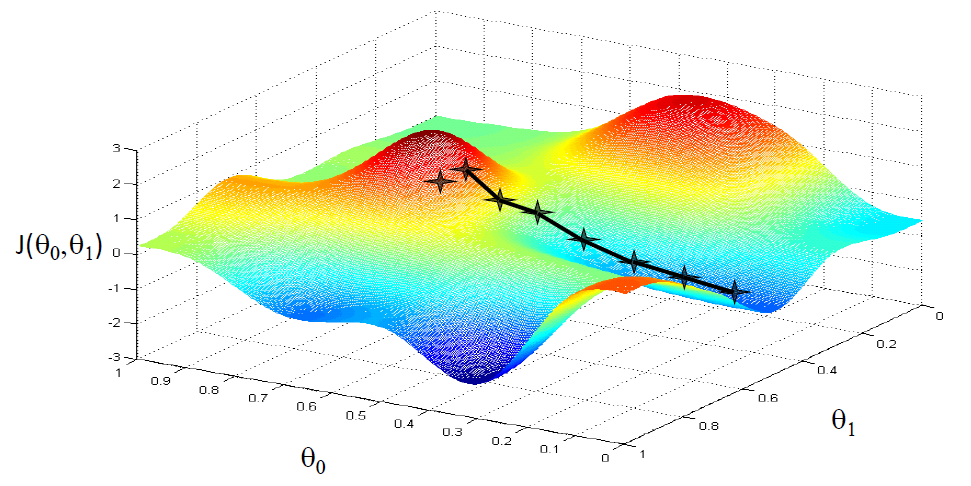
下图使用梯度下降能到达局部最小值
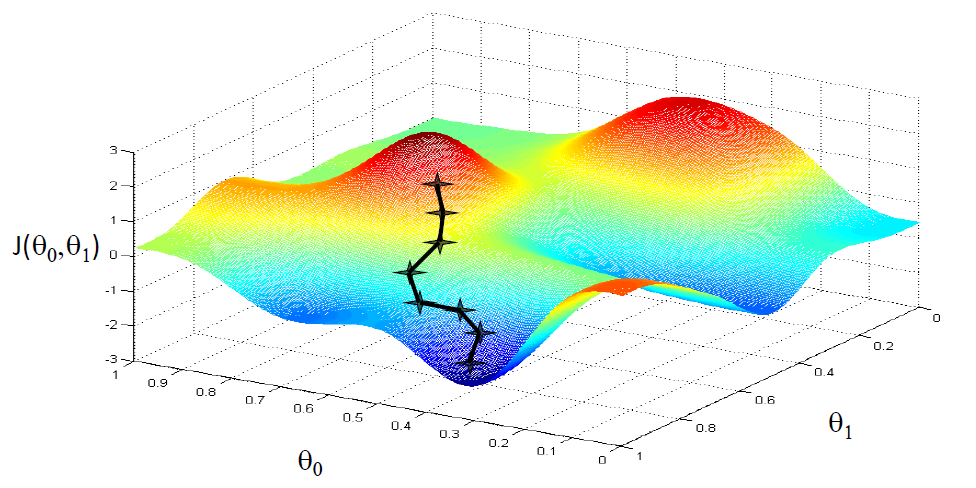
下图使用梯度下降能到达全局最小值
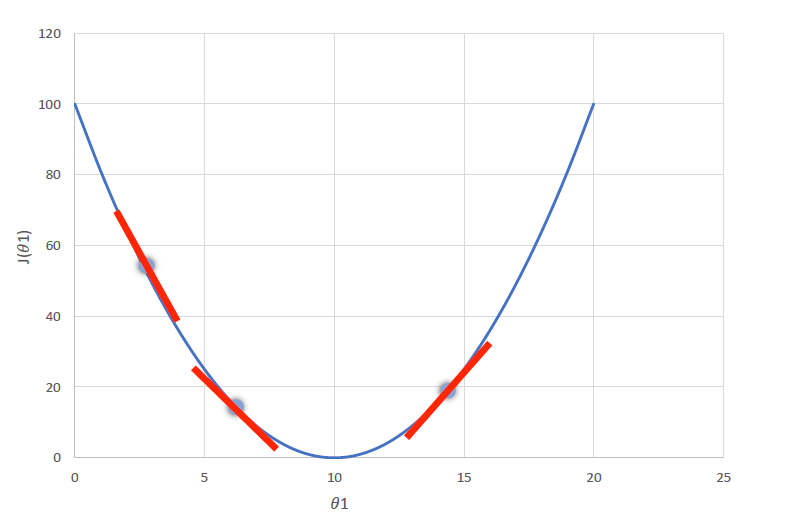
下图中,将 θ 1 \theta1 θ1看成 ω \omega ω, J ( θ 1 ) J(\theta 1) J(θ1)看成 C ( ω , b ) C(\omega,b) C(ω,b)。则
- 在第一个点处, ∂ C ( ω , b ) ∂ ω \frac{\partial C(\omega,b)}{\partial \omega} ∂ω∂C(ω,b)小于0,根据梯度下降公式,此时 ω \omega ω的值会增大,即往代价函数最小值的方向靠近。
- 在第三个点处,
∂
C
(
ω
,
b
)
∂
ω
\frac{\partial C(\omega,b)}{\partial \omega}
∂ω∂C(ω,b)大于0,根据梯度下降公式,此时
ω
\omega
ω的值会减小,即往代价函数最小值的方向靠近。
1.2 多元线性回归
定义多元线性方程
y
=
ω
1
x
1
+
ω
2
x
2
+
.
.
.
+
ω
n
x
n
+
b
y=\omega_1 x_1+\omega_2 x_2+...+\omega_n x_n+b
y=ω1x1+ω2x2+...+ωnxn+b
误差平方和
C
(
ω
1
,
.
.
.
,
ω
n
,
b
)
=
1
2
n
∑
i
=
1
n
(
y
^
(
x
i
)
−
y
i
)
2
C(\omega_1,...,\omega_n,b)=\frac{1}{2n}\sum_{i=1}^n(\hat{y}(x^i)-y^i)^2
C(ω1,...,ωn,b)=2n1i=1∑n(y^(xi)−yi)2
注:
y
^
(
x
i
)
\hat{y}(x^i)
y^(xi)为预测值,
y
i
y^i
yi为真实值,这里的
x
i
x^i
xi表示的是第
i
i
i个数据(包含多列属性)。
由1.1可得
b
:
=
b
−
α
1
n
∑
i
=
1
n
(
y
^
(
x
i
)
−
y
i
)
2
x
0
i
b:=b-\alpha \frac{1}{n}\sum_{i=1}^n(\hat{y}(x^i)-y^i)^2x_0^i
b:=b−αn1i=1∑n(y^(xi)−yi)2x0i
这里
x
0
i
=
1
x^i_0=1
x0i=1,以实现格式统一。
ω
1
:
=
ω
1
−
α
1
n
∑
i
=
1
n
(
y
^
(
x
i
)
−
y
i
)
2
x
1
i
\omega_1:=\omega_1-\alpha \frac{1}{n}\sum_{i=1}^n(\hat{y}(x^i)-y^i)^2x^i_1
ω1:=ω1−αn1i=1∑n(y^(xi)−yi)2x1i
ω
2
:
=
ω
2
−
α
1
n
∑
i
=
1
n
(
y
^
(
x
i
)
−
y
i
)
2
x
2
i
\omega_2:=\omega_2-\alpha \frac{1}{n}\sum_{i=1}^n(\hat{y}(x^i)-y^i)^2x^i_2
ω2:=ω2−αn1i=1∑n(y^(xi)−yi)2x2i
.
.
.
...
...
ω
n
:
=
ω
n
−
α
1
n
∑
i
=
1
n
(
y
^
(
x
i
)
−
y
i
)
2
x
n
i
\omega_n:=\omega_n-\alpha \frac{1}{n}\sum_{i=1}^n(\hat{y}(x^i)-y^i)^2x^i_n
ωn:=ωn−αn1i=1∑n(y^(xi)−yi)2xni
改写为矢量版本
y
=
ω
T
x
y=\omega ^Tx
y=ωTx
ω
:
=
ω
−
α
1
n
X
T
(
y
^
(
x
)
−
y
)
\omega:=\omega-\alpha \frac{1}{n} X^T(\hat{y}(x)-y)
ω:=ω−αn1XT(y^(x)−y)
其中,
ω
\omega
ω和
x
x
x(某行数据)均为列向量,实际应用。
1.3 标准方程法
调用sklearn实现一元线性回归与多元线性回归的梯度下降时,sklearn内部的实现并没有使用梯度下降法,而是使用标准方程法。
公式推导(利用最小二乘法)12

上述公式推导使用到的矩阵求导公式
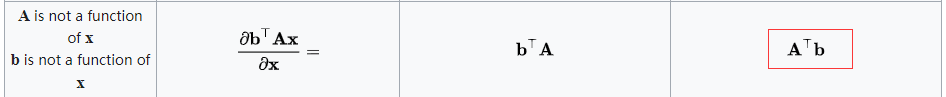

由推导的公式可知,需要满足的条件是
(
X
T
X
)
−
1
(X^TX)^{-1}
(XTX)−1存在。在机器学习中,
(
X
T
X
)
−
1
(X^TX)^{-1}
(XTX)−1不可逆的原因通常有两种,一种是自变量间存在高度多重共线性,例如两个变量之间成正比(例如:x1 为房子的面积,单位是平方英尺;x2为房子的面积,单位是平方米;而1
平方英尺=0.0929 平方米),那么在计算
(
X
T
X
)
−
1
(X^TX)^{-1}
(XTX)−1时,可能得不到结果或者结果无效;另一种则是当特征变量过多(样本数 m
≤
\le
≤特征数量 n)的时候也会导致
(
X
T
X
)
−
1
(X^TX)^{-1}
(XTX)−1不可逆。
(
X
T
X
)
−
1
(X^TX)^{-1}
(XTX)−1不可逆的情况很少发生,如果有这种情况,其解决问题的方法之一便是使用正则化以及岭回归等来求最小二乘法。
单变量情况下利用最小二乘法求解最佳参数

1.4 梯度下降法与标准方程法的优缺点
梯度下降法
优点
- 当特征值非常多的时候也可以很好的工作
缺点
- 需要选择合适的学习率
- 需要迭代多个周期
- 只能得到最优解的近似值
标准方程法
优点
- 不需要学习率不需要迭代可以得到全局最优解
缺点
- 需要计算 ( X T X ) − 1 (X^TX)^{-1} (XTX)−1,时间复杂度大约是 O ( n 3 ) O(n^3) O(n3),n是特征数量
2. 相关系数与决定系数
常用相关系数来衡量两个变量间的相关性,相关系数越大,相关性越高,使用直线拟合样本点时效果就越好。
公式如下(两个变量的协方差除以标准差的乘积)
r
(
X
,
Y
)
=
C
o
v
(
X
,
Y
)
V
a
r
[
X
]
V
a
r
[
Y
]
r(X,Y)=\frac{Cov(X,Y)}{\sqrt{Var[X]Var[Y]}}
r(X,Y)=Var[X]Var[Y]Cov(X,Y)
=
∑
i
=
1
n
(
X
i
−
X
ˉ
)
(
Y
i
−
Y
ˉ
)
∑
i
=
1
n
(
X
i
−
X
ˉ
)
2
∑
i
=
1
n
(
Y
i
−
Y
ˉ
)
2
=\frac{\sum_{i=1}^n(X_i-\bar{X})(Y_i-\bar{Y})}{\sqrt{\sum_{i=1}^n(X_i-\bar{X})^2}\sqrt{\sum_{i=1}^n(Y_i-\bar{Y})^2}}
=∑i=1n(Xi−Xˉ)2∑i=1n(Yi−Yˉ)2∑i=1n(Xi−Xˉ)(Yi−Yˉ)
下图的样本点中,左图的相关系数为0.993,右图的相关系数为0.957,即左图的样本点变量间的相关性更高。
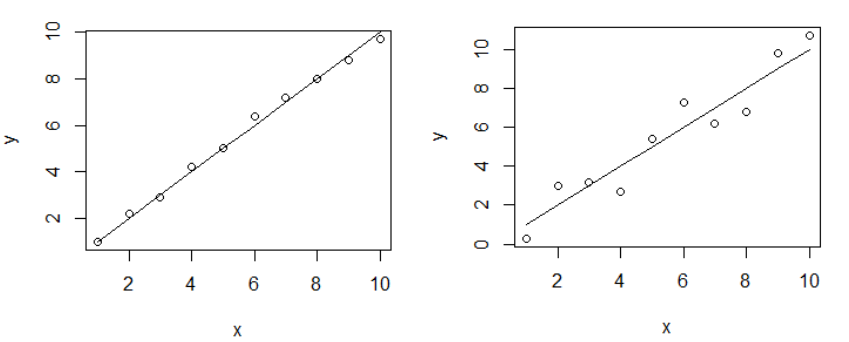
相关系数用于描述两个变量之间的线性关系,但决定系数
R
2
R^2
R2的适用范围更广,可以用于描述非线性或者有两个及两个以上自变量的相关关系,它可以用来评价模型的效果。
总平方和(SST)
∑
i
=
1
n
(
y
i
−
y
ˉ
)
2
\sum_{i=1}^{n}(y_i-\bar{y})^2
i=1∑n(yi−yˉ)2
回归平方和(SSR)
∑
i
=
1
n
(
y
^
−
y
ˉ
)
2
\sum_{i=1}^{n}(\hat{y}-\bar{y})^2
i=1∑n(y^−yˉ)2
残差平方和(SSE)
∑
i
=
1
n
(
y
i
−
y
^
)
2
\sum_{i=1}^{n}(y_i-\hat{y})^2
i=1∑n(yi−y^)2
三者的关系
S
S
T
=
S
S
R
+
S
S
E
SST=SSR+SSE
SST=SSR+SSE
决定系数
R
2
=
S
S
R
S
S
T
=
1
−
S
S
E
S
S
T
=
∑
i
=
1
n
(
y
i
−
y
^
)
2
∑
i
=
1
n
(
y
i
−
y
ˉ
)
2
R^2=\frac{SSR}{SST}=1-\frac{SSE}{SST}=\frac{\sum_{i=1}^{n}(y_i-\hat{y})^2}{\sum_{i=1}^{n}(y_i-\bar{y})^2}
R2=SSTSSR=1−SSTSSE=∑i=1n(yi−yˉ)2∑i=1n(yi−y^)2
R 2 R^2 R2的取值范围在0到1之间,值为0表示模型无法解释因变量的变化,值为1表示模型完全解释了因变量的变化。
覃秉丰——标准方程法 ↩︎
白板推导——最小二乘法及其几何意义 ↩︎
![[LeetCode]-225. 用队列实现栈-232. 用栈实现队列](https://img-blog.csdnimg.cn/6fe972f020854c14b111f172f0196d4e.png)