题目:
1236. 递增三元组 - AcWing题库
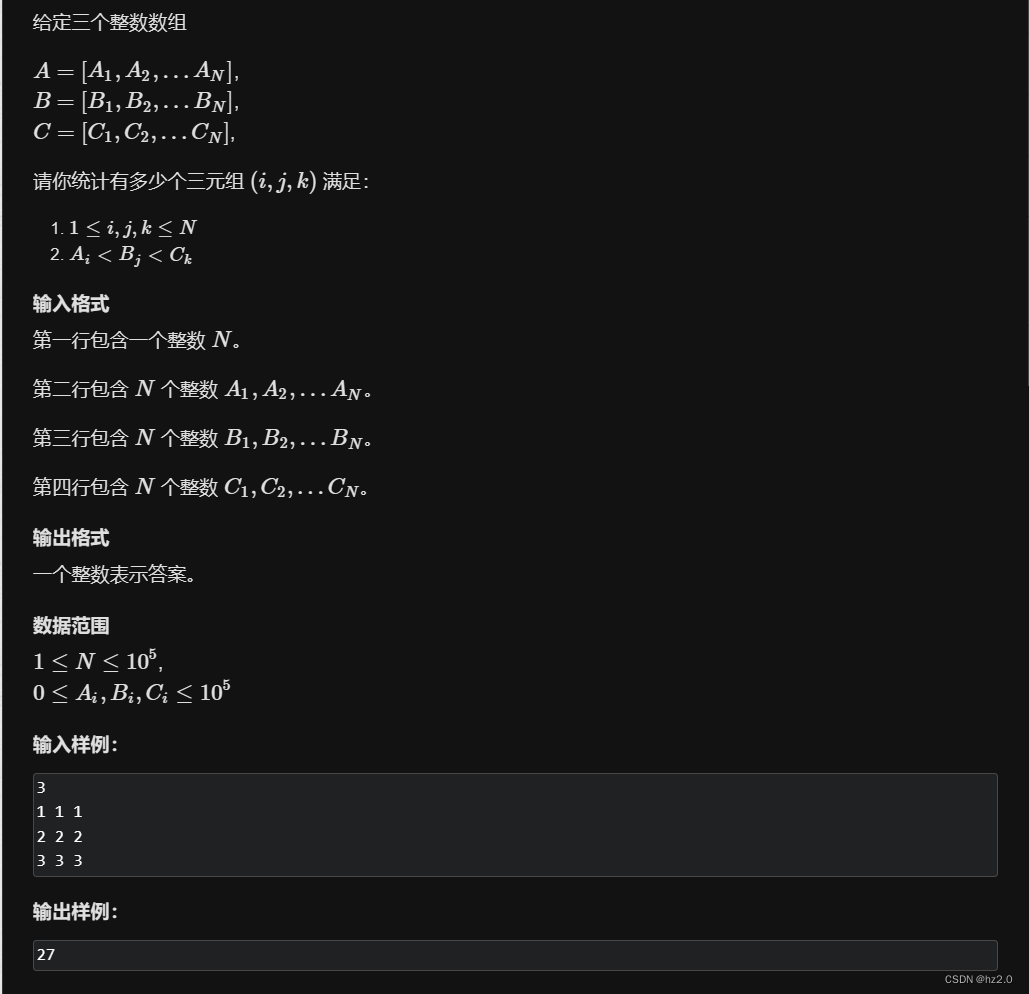
思路:枚举
1.由给定数据估计时间复杂度。
数据范围为1~1e5---->时间复杂度只能为O(n)或者O(nlogn)。
2.先暴力枚举找到思路,再设法优化。
只枚举中间的数组B。对于枚举的每一个bi,找出在A中比其小的a的数量cntA,在C中比其大的c的数量cntC。 cntA*cntC即为当b=bi时的所以满足条件的组合。
法一:二分
1.将A,B数组从小到大排序(sort)
2.明确目标:在A中寻找最后一个小于bi的a的下标,在C中寻找第一个大于bi的c的下标。将二者作为两次二分的分界点。
3.边界情况:当A中没有比bi小的数时,cntA=0;当C中没有比bi大的数时,cntC=0。
代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
int a[N], b[N], c[N];
int n;
int main()
{
cin >> n;
int i;
for (i = 0; i < n; i++)scanf("%d", &a[i]);
for (i = 0; i < n; i++)scanf("%d", &b[i]);
for (i = 0; i < n; i++)scanf("%d", &c[i]);
//排序
sort(a, a + n);
sort(c, c + n);
int cntA = 0, cntC = 0; ll cnt = 0;
for (i = 0; i < n; i++) //遍历数组B
{
//确定最后一个小于bi的a的下标
int L = 0, R = n - 1;
while (L < R) {
int mid = L + R +1>> 1;
if (b[i] > a[mid])L = mid;
else R = mid-1;
}
cntA=L+1;
//边界情况:当A中没有比bi小的数时,cntA=0
if(a[0]>=b[i])cntA=0;
//cout<<cntA;
//确定第一个大于bi的c的下标
L = 0; R = n - 1;
while (L < R) {
int mid = L + R >> 1;
if (b[i] < c[mid])R = mid;
else L = mid+1;
}
cntC=n-L;
//边界情况:当C中没有比bi大的数时,cntC=0
if(b[i]>=c[n-1])cntC=0;
//cout<<cntC<<endl;
cnt += (ll)cntA * cntC;
}
cout << cnt;
}法二:前缀和
1.前缀和本质:以空间换时间。
2.注意:s[i]前缀和求的是前数值从1~i的和,而非数组从a[0]~a[i](或者c[0]~c[i]的和)!!!
3.为确保数组下标>=0,将所以的数值+1(不影响大小比较,但却避免了递归求前缀和时s[i-1]下标为负)
代码:
#include<iostream>
#include<cstdio>
#include<cstring>//memset头文件
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N], c[N];
int Count[N];//表示每个数出现的次数(让数组A(C)的值等于cnt的下标-->字典)
int s[N];//求cnt[]的前缀和
int cntA[N], cntC[N];//分别表示A[],C[]中有多少个数小于b[i]
int main()
{
int n;
cin >> n;
int i;
for (i = 0; i < n; i++)scanf("%d", &a[i]), a[i]++;//统一加一不影响大小比较
for (i = 0; i < n; i++)scanf("%d", &b[i]), b[i]++;//因为要以数值作为下标
for (i = 0; i < n; i++)scanf("%d", &c[i]), c[i]++;//这样可以避免后面当i为1时s[i-1]的下标为负而报错
//求cntA[]
for (i = 0; i < n; i++)Count[a[i]]++;//此时i为下标,表示数值a[i]出现的次数
for (i = 1; i < N; i++)s[i] = s[i - 1] + Count[i];//此时i为大小,表示(数值从1~i出现的次数)经过加一后数值最小为1而不是0
for (i = 0; i < N; i++)cntA[i] = s[b[i] - 1];//此时i为下标,表示A中比数值b[i]小的数的个数
//清空弹夹
memset(Count, 0, sizeof(Count));
memset(s, 0, sizeof(s));
//求cntC[]
for (i = 0; i < n; i++)Count[c[i]]++;
for (i = 1; i < N; i++)s[i] = s[i - 1] + Count[i];
for (i = 0; i < n; i++)cntC[i] = s[N-1] - s[b[i]];//此时i为下标,表示C中比数值b[i]大的数的个数
//枚举每个b[i]
long long res = 0;
for (i = 0; i < n; i++)res += (long long)cntA[i] * cntC[i];
cout << res;
return 0;
}