目录
225. 用队列实现栈
题目
思路
代码
232. 用栈实现队列
题目
思路
代码
225. 用队列实现栈
225. 用队列实现栈 - 力扣(LeetCode)![]() https://leetcode.cn/problems/implement-stack-using-queues/description/
https://leetcode.cn/problems/implement-stack-using-queues/description/
题目
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(
push、top、pop和empty)。实现
MyStack类:
void push(int x)将元素 x 压入栈顶。int pop()移除并返回栈顶元素。int top()返回栈顶元素。boolean empty()如果栈是空的,返回true;否则,返回false。
示例:

思路
- 两个队列,每次要删除数据时,把不删除的数据先导到另一个队列,留下的数据刚好从队头开始删除。。
- 入队列时,入不为空的队列。出队列时,不为空队列的前N-1个数据倒入空队列中,剩下的就在队头,方便删除。
图示:

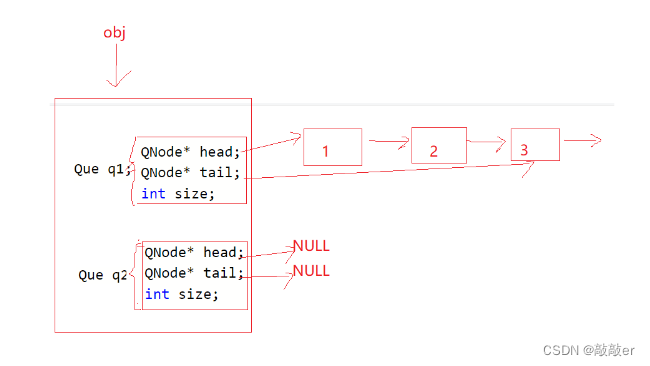
代码
//链式结构:表示队列
typedef int QDataType;
typedef struct QueueNode
{
struct QueueNode* next;
QDataType data;
}QNode;
//队列的结构
typedef struct Queue
{
QNode* head;
QNode* tail;
int size;
}Que;
//初始化队列
void QueueInit(Que* pq);
//销毁队列
void QueueDestroy(Que* pq);
//队尾入队列
void QueuePush(Que* pq, QDataType x);
//队头出队列
void QueuePop(Que* pq);
//获取队列队头元素
QDataType QueueFront(Que* pq);
//获取队列队尾元素
QDataType QueueBack(Que* pq);
//检测队列是否为空,如果为空返回非零结果,如果非空返回0
bool QueueEmpty(Que* pq);
//检测队列中有效元素个数
int QueueSize(Que* pq);
void QueueInit(Que* pq)
{
assert(pq);
pq->head = pq->tail = NULL;
pq->size = 0;
}
void QueueDestroy(Que* pq)
{
assert(pq);
QNode* cur = pq->head;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
pq->size = 0;
}
void QueuePush(Que* pq, QDataType x)
{
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
if (pq->tail == NULL)
{
pq->head = pq->tail = newnode;
}
else
{
pq->tail->next = newnode;
pq->tail = newnode;
}
pq->size++;
}
void QueuePop(Que* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
if (pq->head->next == NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
else
{
QNode* next = pq->head->next;
free(pq->head);
pq->head = next;
}
pq->size--;
}
QDataType QueueFront(Que* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->head->data;
}
QDataType QueueBack(Que* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->tail->data;
}
bool QueueEmpty(Que* pq)
{
assert(pq);
return pq->head == NULL;
}
int QueueSize(Que* pq)
{
assert(pq);
return pq->size;
}
typedef struct {
Que q1;
Que q2;
} MyStack;
MyStack* myStackCreate() {
MyStack* pst=(MyStack*)malloc(sizeof(MyStack));
QueueInit(&pst->q1);
QueueInit(&pst->q2);
return pst;
}
void myStackPush(MyStack* obj, int x) {
if(!QueueEmpty(&obj->q1))
{
QueuePush(&obj->q1,x);
}
else
{
QueuePush(&obj->q2,x);
}
}
int myStackPop(MyStack* obj) {
Que* empty=&obj->q1;
Que* nonEmpty=&obj->q2;
if(!QueueEmpty(&obj->q1))
{
nonEmpty=&obj->q1;
empty=&obj->q2;
}
while(QueueSize(nonEmpty)>1)
{
QueuePush(empty,QueueFront(nonEmpty));
QueuePop(nonEmpty);
}
int top=QueueFront(nonEmpty);
QueuePop(nonEmpty);
return top;
}
int myStackTop(MyStack* obj) {
if(!QueueEmpty(&obj->q1))
{
return QueueBack(&obj->q1);
}
else
{
return QueueBack(&obj->q2);
}
}
bool myStackEmpty(MyStack* obj) {
return QueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);
}
void myStackFree(MyStack* obj) {
QueueDestroy(&obj->q1);
QueueDestroy(&obj->q2);
free(obj);
}
232. 用栈实现队列
232. 用栈实现队列 - 力扣(LeetCode)![]() https://leetcode.cn/problems/implement-queue-using-stacks/description/
https://leetcode.cn/problems/implement-queue-using-stacks/description/
题目
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(
push、pop、peek、empty):实现
MyQueue类:
void push(int x)将元素 x 推到队列的末尾int pop()从队列的开头移除并返回元素int peek()返回队列开头的元素boolean empty()如果队列为空,返回true;否则,返回false
示例:

思路
- 两个栈分别为pushst和popst,pushst负责插入,popst负责删除。
- 插入时往pushst插入。要删除时,先将pushst中的元素一个一个移出往popst中导入,再从栈顶删除,实现先入先出。
- 再要插入时,往pushst插入,
- 再要删除时,先检测popst里面是否还有元素,还有就等popst里面删完了再把pushst导入popst继续删。
popst的栈顶相当于队头,pushst的栈顶相当于队尾。
图示:

代码
#include<stdio.h>
#include<assert.h>
#include<string.h>
#include<stdlib.h>
#include<stdbool.h>
// 下面是定长的静态栈的结构,实际中一般不实用,所以我们主要实现下面的支持动态增长的栈
//静态栈
typedef int STDataType;
#define N 10
typedef struct Stack
{
STDataType _a[N];
int _top; // 栈顶
}Stack;
//动态栈 支持动态增长的栈
typedef int STDataType;
typedef struct stack
{
STDataType* a;
int top;//栈顶
int capacity;//容量
}ST;
//初始化栈
void STInit(ST* ps);
//销毁栈
void STDestroy(ST* ps);
//入栈
void STPush(ST* ps, STDataType x);
//出栈
void STPop(ST* ps);
//获取栈顶元素
STDataType Sttop(ST* ps);
//获取栈中有效元素
int STSize(ST* ps);
//检测栈中是否为空
bool STEmpty(ST* ps);
//̬ջʼ
void STInit(ST* ps)
{
assert(ps);
ps->a = NULL;
ps->capacity = 0;//
ps->top = 0;//ջ
}
//
void STDestroy(ST* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->top = ps->capacity = 0;
}
//
void STPush(ST* ps, STDataType x)
{
assert(ps);
if (ps->top == ps->capacity)
{
int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
ps->a = tmp;
ps->capacity = newCapacity;
}
ps->a[ps->top] = x;
ps->top++;
}
//ɾ
void STPop(ST* ps)//, STDataType x
{
assert(ps);
assert(ps->top > 0);
--ps->top;
}
STDataType STTop(ST* ps)
{
assert(ps);
assert(ps->top > 0);
return ps->a[ps->top - 1];
}
int STSize(ST* ps)
{
assert(ps);
return ps->top;
}
bool STEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
typedef struct {
ST pushst;
ST popst;
} MyQueue;
MyQueue* myQueueCreate() {
MyQueue* obj=(MyQueue*)malloc(sizeof(MyQueue));
STInit(&obj->pushst);
STInit(&obj->popst);
return obj;
}
void myQueuePush(MyQueue* obj, int x) {
STPush(&obj->pushst,x);//直接往pushst插入
}
int myQueuePop(MyQueue* obj) {
int front=myQueuePeek(obj);
STPop(&obj->popst);
return front;
}
int myQueuePeek(MyQueue* obj) {
if(STEmpty(&obj->popst))
{
//倒数据
while(!STEmpty(&obj->pushst))
{
STPush(&obj->popst,STTop(&obj->pushst));
STPop(&obj->pushst);
}
}
return STTop(&obj->popst);
}
bool myQueueEmpty(MyQueue* obj) {
return STEmpty(&obj->popst)&&STEmpty(&obj->pushst);
}
void myQueueFree(MyQueue* obj) {
STDestroy(&obj->popst);
STDestroy(&obj->pushst);
free(obj);
}