《算法通关村——二分查找在旋转数字中的应用》

news2024/9/21 2:38:28

《算法通关村——二分查找在旋转数字中的应用》

这里我们直接通过一个题目，来了解二分查找的应用。

153. 寻找旋转排序数组中的最小值

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次旋转后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

示例 3：

输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

提示：

n == nums.length
1 <= n <= 5000
-5000 <= nums[i] <= 5000
nums 中的所有整数 互不相同
nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

理解

无论经过多少次旋转，我们可以理解以下，整个数列肯定是呈现出一个这样子的情况：从开始的地方一直递增，然后突然就到了最小值，然后从最小值之后有递增，到了数列的最后一个值，因为从题目可以得知，数列的数字是唯一且递增的，所以可以确认数列（除非是原数列的次序）第一个值肯定比第二个值大。通过一个图来理解以下。通过上面的文字和这个图以下就明了了。

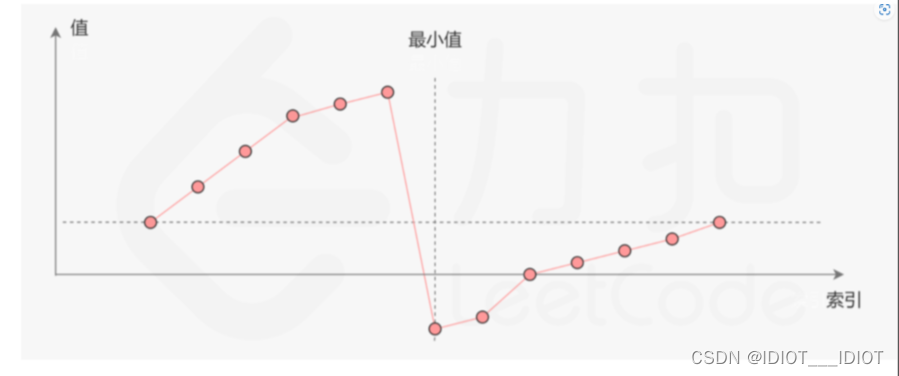
在这里插入图片描述

虽然了解了是这么一种次序，但如何去和二分挂钩呢，因为我们今天的主题可是二分啊。别急我们慢慢道来。

我们可以定义low（低索引），high（高索引），和pivot（中间值）三个变量。有以下三种情况，1.中间值比高位置小，而最小值在位置更小的地方，高位要往低位走，如图
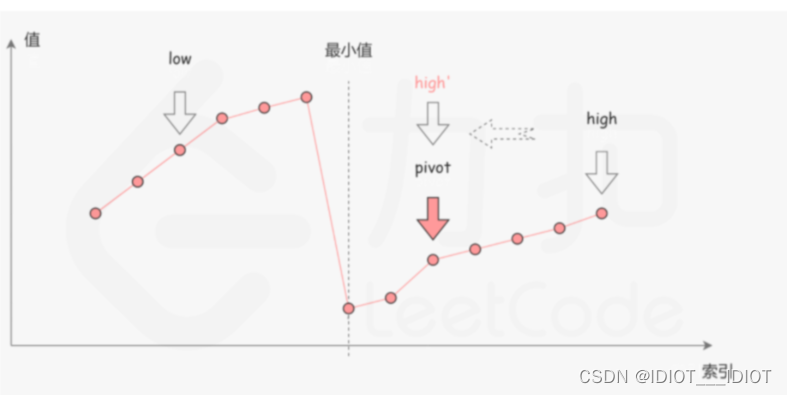
在这里插入图片描述

2.中间值比高位置大，而最小值在更高的位置，低位要往高位走。如图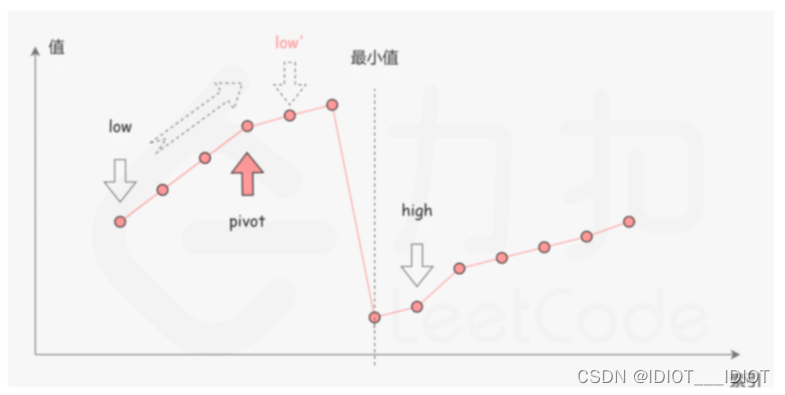在这里插入图片描述

3.另外就是相等了。通过此就可以定义递归。

必须注意的是low=pivot+1，而high=pivot，可以通过[3,1,2]理解，这里就不详细说啦。

题解代码

class Solution {
    public int findMin(int[] nums) {
        int low = 0;
        int high = nums.length-1;
        while(low < high){
            int pivot = low + ((high - low)>>1);
            if(nums[pivot] < nums[high]){
                high = pivot;
            }
            if(nums[pivot] > nums[high]){
                low = pivot + 1;
            }
        }
        return nums[low];
    }
}