报名明年4月蓝桥杯软件赛的同学们，如果你是大一零基础，目前懵懂中，不知该怎么办，可以看看本博客系列：备赛20周合集
20周的完整安排请点击：20周计划
每周发1个博客，共20周（读者可以按自己的进度选“正常”和“快进”两种计划）。
每周3次集中答疑，周三、周五、周日晚上，在QQ群上答疑：

第 4周:  杂题-2

0. 上周答疑

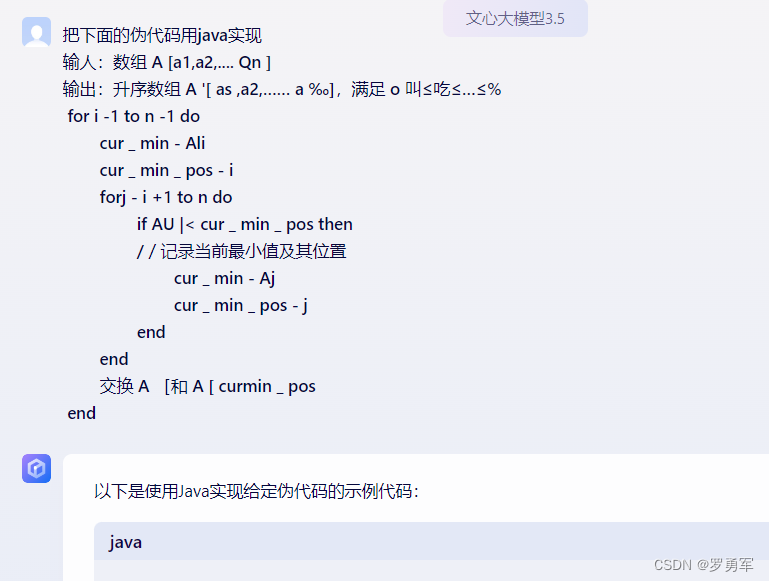
  伪代码怎么转化Java语言？
  C/C++、Java、Python代码怎么互转？
  回答：用大数据模型转，例如文心一言3.5，是免费的。
  在转换代码这件事上，大数据模型做得很好。

1. 精讲题

  本周还是杂题！
  大家是不是感到太慢了，什么时候才学数据结构、算法呢？我想立刻现在马上学：二分、排序、二叉树、DFS、…
  不要着急，杂题做得越多，后面的学习越高效越快！
  一是提高编码能力！争取做到：一次写20行代码，不用调试一次过！
  二是算法能力！杂题虽然没用到经典算法，但它们的解题步骤其实也是算法，有时难度不亚于经典算法。
  下面给出6个精讲题，有模拟、构造、思维、数学等各种杂题，难度从简单到难。大家自己先做，然后再看题解。

1.1 修剪灌木

难度 **
2022年第十三届省赛：链接1-蓝桥OJ 、链接2-NewOj
【题解】这是一道思维题。由于每棵灌木都会在2N天内被剪为0，所以不会无限长高。其中的第i棵，它左边有i-1棵，右边有n-i棵。爱丽丝分别从左右绕回来，各需要2i和2(n-i-1)天，取最大值就是高度。i从0开始。
（1）C/C++代码

#include<bits/stdc++.h>
using namespace std;
int main() {
    int n;  cin >> n;
    for (int i = 0; i < n; i++)   cout << max(i, n - i - 1) * 2 << endl;
    return 0;
}

（2）python代码

n = int(input())
for i in range (n): print(max(i,n-i-1)*2)

（3）java代码

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        for (int i = 0; i < n; i++) {
            System.out.println(Math.max(i, n - i - 1) * 2);
        }
    }
}

1.2 英文数字计数

见博客：英文数字计数
难度 ***

1.3 矩形拼接

2022年第十三届省赛: 链接-NewOJ
难度 *** 准确地说，难度有3.5颗星
【题解】本题是一道纯粹的构造题，思维简单，但是代码比较繁琐细致，目的是考核编码能力。
  3个矩形摆在一起，可能有几个边？读者可以在纸上手画观察，如果3个矩形完全不能匹配，是8边形；如果能完全匹配成一个新矩形，是4边形；其他情况是6边形。
  本题只有3个矩形，并不复杂。3个矩形做任意组合，每个矩形有横竖两种摆法，共48种情况。T = 1000组测试，总计算量是1000×48，计算量很小不会超时，所以简单地用暴力法组合出所有情况，取最小值即可。
（1）C/C++代码
  下面的C++代码，第10 ~ 14行，对3个矩形进行组合。第15 ~ 17行，每个矩形有横和竖两种摆法。
  第18行，如果一个矩形的边长等于另外两个矩形边长之和，那么至少是6个边。然后第20行，如果这两个矩形边长相等，那么就是4个边。后面几行请自己分析。

#include<bits/stdc++.h>
using namespace std;
int a[3][2];
int main(){
    int T;    cin >> T;
    while(T--)    {
        for(int i = 0; i < 3; i++)
            cin >> a[i][0] >> a[i][1];
        int ans = 8;
        for(int i = 0; i < 3; i++)               //第1个矩形
            for(int j = 0; j < 3; j++)
                if(i != j)                       //第2个矩形
                    for(int k = 0; k < 3; k++)
                        if(k != i && k != j)     //第3个矩形
                            for(int ii = 0; ii <= 1; ii++){           //第1个有横竖两种摆法
                                for(int jj = 0; jj <= 1; jj++){       //第2个横竖摆
                                    for(int kk = 0; kk <= 1; kk++){   //第3个横竖摆
                                        if(a[i][ii] == a[j][jj] + a[k][kk]){ 
                                            ans = min(ans, 6);
                                            if(a[j][1-jj] == a[k][1-kk])
                                                ans = min(ans, 4);
                                        }
                                        if(a[i][ii] == a[j][jj] || a[j][jj] == a[k][kk])
                                            ans = min(ans, 6);
                                        if(a[i][ii] == a[j][jj] && a[j][jj] == a[k][kk])
                                            ans = min(ans, 4);
                                    }
                                }
                            }
        cout<<ans<<endl;
    }
    return 0;
}

（2）python代码

def check1(x1,x2,x3):
    if x1>=x2 and x1>=x3:
        if x1==x2+x3 and a[2]+a[3]-x2==a[4]+a[5]-x3:  return True
    if x2>=x1 and x2>=x3:
        if x2==x1+x3 and a[0]+a[1]-x1==a[4]+a[5]-x3:  return True
    if x3>=x1 and x3>=x2:
        if x3==x1+x2 and a[0]+a[1]-x1==a[2]+a[3]-x2:  return True
    return False
def check2(x1,x2,x3):
    if x1>=x2 and x1>=x3:
        if x1==x2+x3:    return True
    if x2>=x1 and x2>=x3:
        if x2==x1+x3:    return True
    if x3>=x1 and x3>=x2:
        if x3==x1+x2:    return True
    return False
     
T = int(input())
for t in range(T):
    a=list(map(int,input().split()))
    ans=8
    for i in range(0,2):              #第1个矩形
        for j in range(2,4):          #第2个矩形
            for k in range(4,6):      #第3个矩形
                x1,x2,x3 = a[i],a[j],a[k]
                if x1==x2 and x2==x3:          ans = min(ans,4)
                if check1(x1,x2,x3):           ans = min(ans,4)
                if x1==x2 or x1==x3 or x2==x3: ans = min(ans,6)
                if check2(x1,x2,x3):           ans = min(ans,6)
    print(ans)

（3）java代码

import java.util.*;
import java.io.*; 
public class Main { 
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int T = in.nextInt();
        for(int _t = 1; _t <= T; _t++){
            int[][] a = new int[3][2];
            int ans = 8;
            for(int i = 0; i < 3; i++) {
                a[i][0] = in.nextInt();
                a[i][1] = in.nextInt();
            }
            //枚举第一个矩形下标为i，第二个矩形下标为j，第三个矩形下标为k
            for(int i = 0; i < 3; i++)
                for(int j = 0; j < 3; j++)
                    if(i != j)
                        for(int k = 0; k < 3; k++)
                            if(i != k && j != k)
                            //枚举三个矩形的两条边
                                for(int ii = 0; ii <= 1; ii++)
                                    for(int jj = 0; jj <= 1; jj++)
                                        for(int kk = 0; kk <= 1; kk++) {
                                            if(a[i][ii] == a[j][jj])//6条边的情况1
                                                ans = Math.min(ans, 6);
                                            if(a[i][ii] == a[j][jj] && a[i][ii] == a[k][kk])//4条边的情况1
                                                ans = Math.min(ans, 4);
                                            //枚举仅考虑a[i][ii] 与 a[j][jj] + a[k][kk]的关系
                                            if(a[i][ii] == a[j][jj] + a[k][kk])  {
                                                ans = Math.min(ans, 6);     //6条边的情况2
                                                if(a[j][1 - jj] == a[k][1 - kk])    //4条边的情况2
                                                    ans = Math.min(ans, 4);
                                            }
                                    }
            System.out.println(ans);
        }
    }
}

1.4 最少砝码

2021年第十二届蓝桥杯省赛: 链接1-蓝桥OJ
难度 ***
【题解】这是一道找规律题。
  题目要求给出最少数量的几个整数（砝码），通过加减组合得到1 ~ N的整数。熟悉二进制的都知道，用1、2、4、8、16、…这些2的倍数，可以组合后相加得到任意整数。不过，本题的砝码不仅可以相加，还可以放在天平的两边通过减法得到新的称重。例如N = 3时，砝码可以是{1, 2}，也可以是{1, 3}、{2, 3}。
  本题的思维有一点难度，读者如果自己提前做了此题，思维过程可能比较繁琐。下面给出一种简洁的推理方法。
  设当前砝码称重范围是1 ~ R。加一个砝码w，并且要求不重复加w前已经能得到的称重，那么w将是一个很大的砝码。新的称重范围是：
    {1, 2, …, R, w-R, w-R+1,…, w, w+1, w+2, …, w+R}
  因为从R到w-R是连续的，所以有w-R = R+1，即w = 2R+1。也就是说，如果当前称重范围是1 ~ R，那么加一个w = 2R+1的砝码，可以扩展到新的称重范围R’= w+R = 3R+1。
  下面列表计算，每一行的“原砝码，原称重范围”是上一行的“新砝码，新称重范围”。

  这个表格给出了一种最少砝码的实现方式，虽然可能有其他实现方式，但这种实现方式最大程度扩展了新的R’，是一种最优方案。
  根据这个表格可以得到计算方法：（1）砝码按3的倍数增长；（2）每加一个砝码，称重范围增长到R’ = 3R+1。
  R按3倍增长，这比二进制的倍增还快，当N = $10^9$时，计算量$lo{g}_{3}N$ < $lo{g}_{2}N$ = 30。

（1）C/C++代码

#include <stdio.h>
int main() {
    int N;
    scanf("%d", &N);
    int R = 1;
    int cnt = 1;
    while (R < N) {
        R = R * 3 + 1;
        cnt++;
    }
    printf("%d", cnt);
    return 0;
}

（2）python代码

N = int(input())
R = 1 
cnt = 1
while R < N:
    R = R*3 + 1
    cnt += 1
print(cnt)

（3）java代码

import java.util.*;
public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int N = scanner.nextInt();
        int R = 1;
        int cnt = 1;
        while (R < N) {
            R = R * 3 + 1;
            cnt++;
        }
        System.out.println(cnt);
    }
}

1.5 蜂巢

2022年第十三届省赛: [链接1-蓝桥OJ]
难度 ****
【题解】本题是一道构造题，考点有两个：坐标转换、距离计算。
  蜂巢有6个方向，看起来比较复杂，但实际上走步非常简单，例如样例中从B走到C，C在B的右下方，B只要一直向右向下走，且不超过C的行和列，不管怎么走，一定能以最小步数走到C。
  本题的难点是对坐标的处理。如果是简单的直角坐标系，很容易计算。本题是六角形的蜂巢，每个蜂巢的中心点是否能转为直角坐标？把蜂巢的关系用下面的直角坐标表示：

  中心点O，对应的6个蜂巢的坐标分别为(-2, 0)、(-1, 1)、(1, 1)、(2, 0)、(1, -1)、(-1, -1)，下面代码中用xdir[]、ydir[]表示。
  先计算得到起点坐标(x1, y1)、终点坐标(x2, y2)。如何计算起点到终点的步数？由于蜂巢的坐标比较奇怪，不能直接用“曼哈顿距离[ 曼哈顿距离，又称为出租车距离：两点的距离等于x方向上的距离加上y方向上的距离，即|x1-x2| + |y1-y2|。]”计算。读者如果已经做了这一题，可能是用各种复杂的判断来计算的。下面给出一个简单巧妙的方法。
  坐标之差的绝对值dx = |x1-x2|，dy = |y1-y2|，有以下结论：
  1、若dx ≥ dy，那么最少步数是(dx+dy)/2，即先横着走，再斜着走；
  2、若dx < dy，一直斜着走就行，最少步数是dy。

（1）C/C++代码
  代码中有一个地方需要注意，即坐标值应该用long long，如果用int会溢出。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll xdir[] = {-2,-1,1,2, 1,-1};  //横向
ll ydir[] = { 0, 1,1,0,-1,-1};  //纵向
void walk(ll d, ll q, ll &x, ll &y){
    x += xdir[d] * q;
    y += ydir[d] * q;           //引用传参，返回坐标值(x,y)
}
int main(){
    ll d1,p1,q1,d2,p2,q2;
    cin>>d1>>p1>>q1>>d2>>p2>>q2;
    ll x1 = 0, y1 = 0;           //计算起点坐标(x1, y1)
    walk(d1,p1,x1,y1);           //先走第1个方向
    walk((d1 + 2) % 6,q1,x1,y1); //再走第2个方向
    ll x2 = 0, y2 = 0;           //计算终点坐标(x2, y2)
    walk(d2,p2,x2,y2);
    walk((d2 + 2) % 6,q2,x2,y2);
    ll dx = abs(x1 - x2), dy = abs(y1 - y2);
    if (dx >= dy) cout << (dx+dy)/2;      //先横走，再斜着走
    else          cout << dy;              //一直斜着走就行了
}

（2）python代码

xdir = [-2,-1,1,2, 1,-1]
ydir = [ 0, 1,1,0,-1,-1]
def walk(d, q,x,y):  
    x += xdir[d]*q
    y += ydir[d]*q
    return x,y
d1,p1,q1,d2,p2,q2 = map(int,input().split())
x1, y1 = walk(d1,p1,0,0)
x1, y1 = walk((d1 + 2) % 6, q1,x1,y1)
x2, y2 = walk(d2,p2,0,0)
x2, y2 = walk((d2 + 2) % 6, q2,x2,y2)
dx,dy = abs(x1 - x2), abs(y1 - y2);
if (dx >= dy): print((dx+dy)//2)     #先横走，再斜着走
else:          print(dy)             #一直斜着走 

（3）java代码

import java.util.*;
public class Main {
    static long[] xdir = {-2, -1, 1, 2, 1, -1}; //横向
    static long[] ydir = {0, 1, 1, 0, -1, -1}; //纵向
    static void walk(int d, long q, long[] pos) {
        pos[0] += xdir[d] * q;
        pos[1] += ydir[d] * q;
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int d1 = scanner.nextInt();
        long p1 = scanner.nextLong();
        long q1 = scanner.nextLong();
        int d2 = scanner.nextInt();
        long p2 = scanner.nextLong();
        long q2 = scanner.nextLong();
        long[] pos1 = {0, 0};
        walk(d1, p1, pos1);
        walk((d1 + 2) % 6, q1, pos1);
        long[] pos2 = {0, 0};
        walk(d2, p2, pos2);
        walk((d2 + 2) % 6, q2, pos2);
        long dx = Math.abs(pos1[0] - pos2[0]);
        long dy = Math.abs(pos1[1] - pos2[1]);
        if (dx >= dy)  System.out.println((dx + dy) / 2);
        else           System.out.println(dy);        
    }
}

1.6 立方体表面距离

见博客：立方体表面距离
难度 *****

2. 刷题

  还是继续刷题吧。上周的题目链接，大家接着做：

  蓝桥题库的模拟题-简单
  蓝桥题库的模拟题-中等
  蓝桥题库的模拟题-困难

  蓝桥题库的枚举题-简单
  蓝桥题库的枚举题-中等
  蓝桥题库的枚举题-困难

  蓝桥题库的递归题