先说结论:机器学习中的正则化主要解决模型过拟合问题。
如果模型出现了过拟合,一般会从两个方面去改善,一方面是训练数据,比如说增加训练数据量,另一方面则是从模型角度入手,比如,降低模型复杂度。
但无论是增加数据量还是降低模型复杂度,都是不容易做到的,这时正则化就是一个唾手可得选择,只要在损失函数中加入正则化项,往往就能得到一个不错的效果提升。
什么是过拟合?
如果模型在训练集上效果好,但在测试集上效果差,这时我们就怀疑模型出现了过拟合。

最左边的是欠拟合,模型过于简单,只能拟合简单的线性关系。
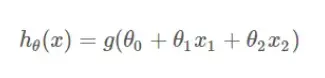
中间的代表刚好拟合,其拟合的是一个2次多项式:
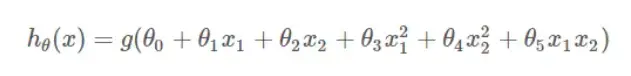
最右边的图就是过拟合的例子,模型过于复杂,也就是说模型考虑的太多了,模型可能使用了与分类无关的特征,或者模型试图去拟合关于特征的M次多项式,最终导致过拟合。
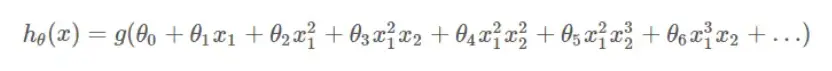
什么是正则化?
以线性回归为例,正常情况下,损失函数是这个样子的:
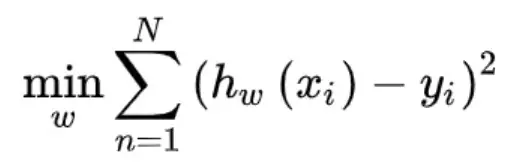
加入正则化项后:
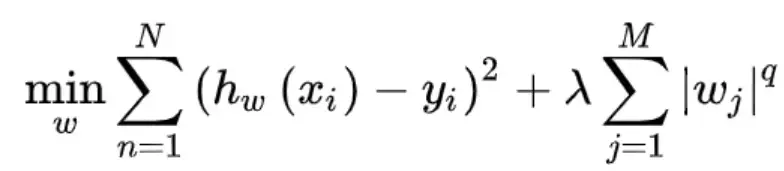
如果q等于1称为L1正则化,q等于2称为L2正则化。
为什么正则化能防止过拟合?
前面我们说过,降低模型复杂度可以防止过拟合,正则化本质上就是在降低模型复杂度,正则化项其实就是对损失函数达到最小值的最优解w进行了限制。
在SVM的推理过程中,我们接触了带约束的最优化问题,并且知道可以通过拉格朗日乘子法以及对偶问题将带等式约束以及不等式约束优化问题转换成不带约束的优化问题。 所以对于公式(2),可以等价为:
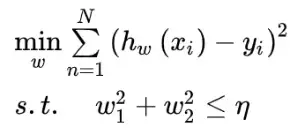
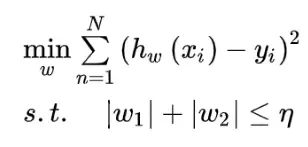
上面的公式可视化为:
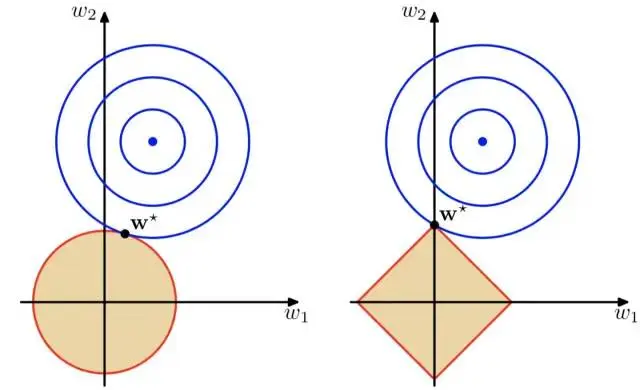
上图,蓝色的圆是原始损失函数(1)的等高线,其中心点是最优解,棕色的代表正则化项,有了正则化项约束后,最优解只能在棕色的圆或者正方形内寻找,所以最优解只能是等高线与圆的切点或者与正方形顶点的交点。
那为什么与正则化项相交点的参数能防止过拟合呢?
先来看L1正则化,最优解w一定是在坐标轴上,也就是说w的某些维度一定是0,这就起到了参数稀疏化的作用。
(在神经网络中的Dropout机制不也是一种正则化思想嘛!)
既然参数的某些元素为0,那么就可能把模型拟合的M次多项式高次项或者组合项去掉转换为2次多项式了。
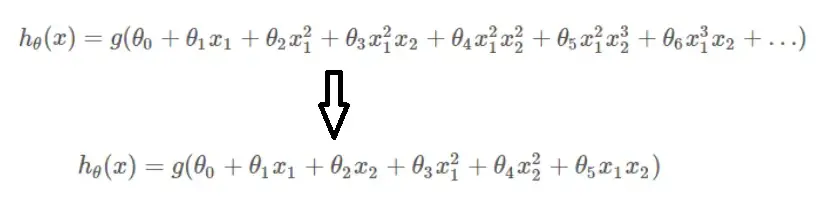
而L2正则化虽然没有使W中的某些元素为0,但却使w的每个元素都很小,也就是限制了某些高次项或者复杂组合项的作用。 所以无论是哪种正则化,都是在约束模型的复杂度。