文章目录
- 数楼梯
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- [NOIP2002 普及组] 过河卒
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- [NOIP2003 普及组] 栈
- 题目背景
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
数楼梯
题目描述
楼梯有 N N N 阶,上楼可以一步上一阶,也可以一步上二阶。
编一个程序,计算共有多少种不同的走法。
输入格式
一个数字,楼梯数。
输出格式
输出走的方式总数。
样例 #1
样例输入 #1
4
样例输出 #1
5
提示
- 对于 60 % 60\% 60% 的数据, N ≤ 50 N \leq 50 N≤50;
- 对于 100 % 100\% 100% 的数据, 1 ≤ N ≤ 5000 1 \le N \leq 5000 1≤N≤5000。
#include <iostream>
#include <string>
#include <cstdlib>
#include <cstring>
using namespace std;
#define maxn 1700
struct Bigint {
int len, a[maxn];
Bigint(int x = 0) {
memset(a, 0, sizeof(a));
for (len = 1; x; len++)
static_cast<void>(a[len] = x % 10), x /= 10;
len--;
}
int& operator[](int i) {
return a[i];
}
void flatten(int L) {
len = L;
for (int i = 1; i <= len; i++) {
a[i + 1] += a[i] / 10;
a[i] %= 10;
}
for (; !a[len];) len--;
}
void print() {
for (int i = max(len, 1); i >= 1; i--)
printf("%d", a[i]);
}
};
Bigint operator+(Bigint a, Bigint b) {
Bigint c;
int len = max(a.len, b.len);
for (int i = 1; i <= len; i++)
c[i] += a[i] + b[i];
c.flatten(len + 1);
return c;
}
int main() {
int N;
cin >> N;
Bigint f[5010];
f[1] = Bigint(1);
f[2] = Bigint(2);
for (int i = 3; i <= N; i++)
f[i] = f[i - 2] + f[i - 1];
f[N].print();
return 0;
}
[NOIP2002 普及组] 过河卒
题目描述
棋盘上 A A A 点有一个过河卒,需要走到目标 B B B 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 C C C 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示, A A A 点 ( 0 , 0 ) (0, 0) (0,0)、 B B B 点 ( n , m ) (n, m) (n,m),同样马的位置坐标是需要给出的。

现在要求你计算出卒从 A A A 点能够到达 B B B 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
输入格式
一行四个正整数,分别表示 B B B 点坐标和马的坐标。
输出格式
一个整数,表示所有的路径条数。
样例 #1
样例输入 #1
6 6 3 3
样例输出 #1
6
提示
对于 100 % 100 \% 100% 的数据, 1 ≤ n , m ≤ 20 1 \le n, m \le 20 1≤n,m≤20, 0 ≤ 0 \le 0≤ 马的坐标 ≤ 20 \le 20 ≤20。
【题目来源】
NOIP 2002 普及组第四题
#include <iostream>
#define NAXN 22
using namespace std;
int ctrl[NAXN][NAXN];
int n, m, hx, hy;
long long f[NAXN][NAXN] = {0};
int dx[9][2] = {{0,0},{1,2},{1,-2},{-1,2},{-1,-2},{2,1},{2,-1},{-2,1},{-2,-1}};
//马的控制范围相对于马位置的偏移
int main(){
cin >> n >> m >> hx >> hy;
for (int i = 0; i < 9; i++){
int tmpx = hx + dx[i][0];
int tmpy = hy + dx[i][1];
//判断在棋盘范围内
if (tmpx >= 0 && tmpx <= n && tmpy >= 0 && tmpy <= m){
ctrl[tmpx][tmpy]=1;//记录马的控制点
}
}
f[0][0] = 1 - ctrl[0][0]; //若原点就是马控制点,则初始路径数量就是0,否则是1
for (int i = 0; i <= n; i++){
for (int j = 0; j <= m; j++){
if(ctrl[i][j]) continue;//若这个点是控制点,则跳过
if (i != 0) f[i][j] += f[i - 1][j]; //若不在横轴上,上面路径数加上
if (j != 0) f[i][j] += f[i][j - 1]; //若不在纵轴上,左边路径数加上
}
}
cout << f[n][m];//输出答案
return 0;
}
[NOIP2003 普及组] 栈
题目背景
栈是计算机中经典的数据结构,简单的说,栈就是限制在一端进行插入删除操作的线性表。
栈有两种最重要的操作,即 pop(从栈顶弹出一个元素)和 push(将一个元素进栈)。
栈的重要性不言自明,任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时,想到了一个书上没有讲过的问题,而他自己无法给出答案,所以需要你的帮忙。
题目描述
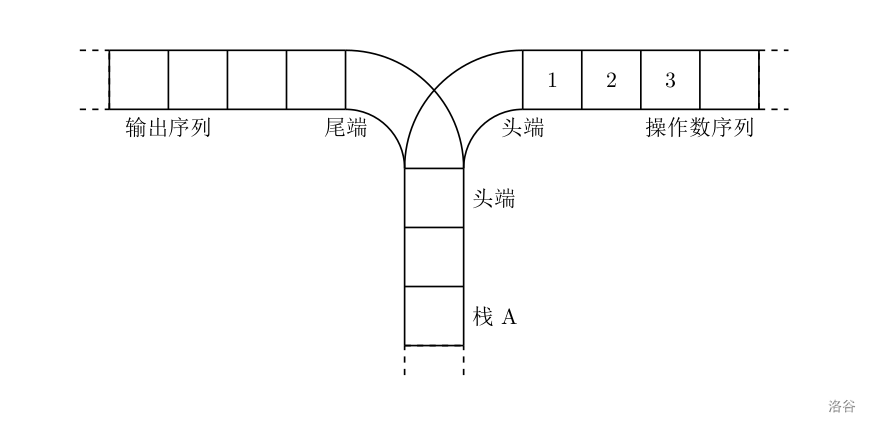
宁宁考虑的是这样一个问题:一个操作数序列, 1 , 2 , … , n 1,2,\ldots ,n 1,2,…,n(图示为 1 到 3 的情况),栈 A 的深度大于 n n n。
现在可以进行两种操作,
- 将一个数,从操作数序列的头端移到栈的头端(对应数据结构栈的 push 操作)
- 将一个数,从栈的头端移到输出序列的尾端(对应数据结构栈的 pop 操作)
使用这两种操作,由一个操作数序列就可以得到一系列的输出序列,下图所示为由 1 2 3 生成序列 2 3 1 的过程。
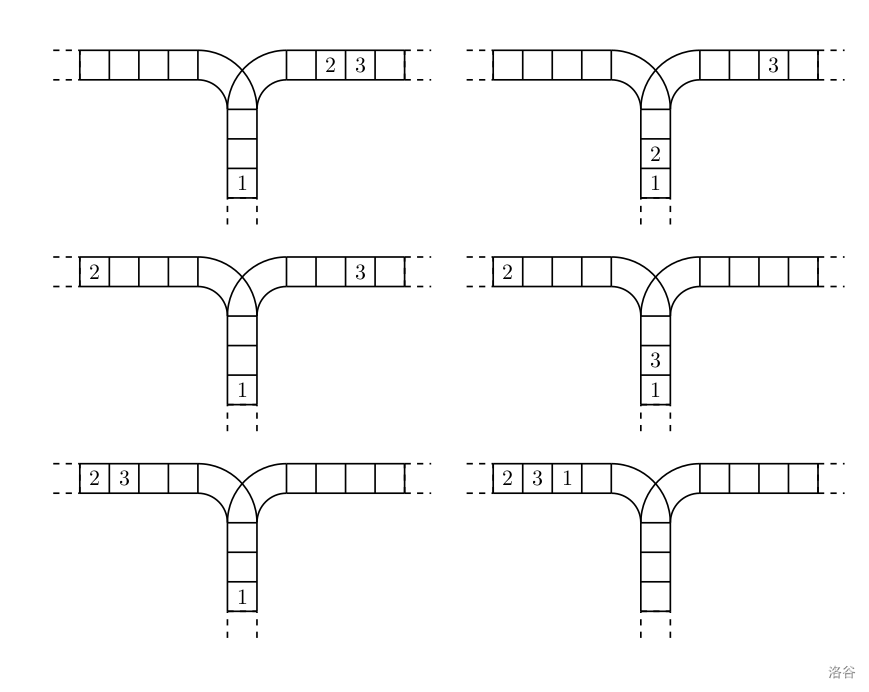
(原始状态如上图所示)
你的程序将对给定的 n n n,计算并输出由操作数序列 1 , 2 , … , n 1,2,\ldots,n 1,2,…,n 经过操作可能得到的输出序列的总数。
输入格式
输入文件只含一个整数 n n n( 1 ≤ n ≤ 18 1 \leq n \leq 18 1≤n≤18)。
输出格式
输出文件只有一行,即可能输出序列的总数目。
样例 #1
样例输入 #1
3
样例输出 #1
5
提示
【题目来源】
NOIP 2003 普及组第三题
#include<cstdio>
using namespace std;
int main(){
int n,h[20]={1,1};
scanf("%d",&n);
for(int i=2;i<=n;i++)
for(int j=0;j<i;j++)
h[i] += h[j]*h[i-j-1];
printf("%d",h[n]);
return 0;
}


![[Machine Learning] 多任务学习](https://img-blog.csdnimg.cn/2cb02ad1b9534645b82c801ba69bbbff.png#pic_center)