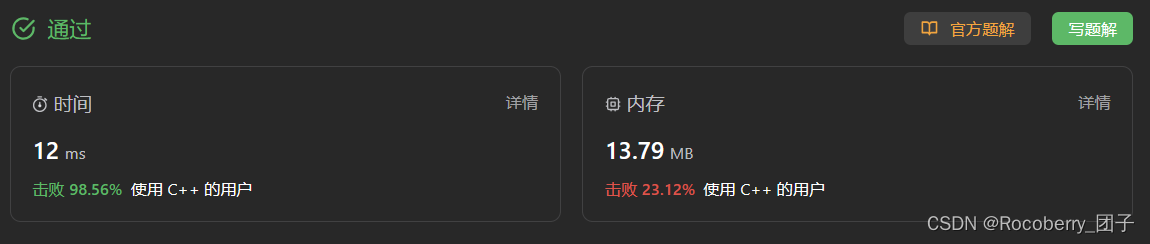
课程表
- 题解1 BFS(拓扑图模板)
- 题解2 DFS
你这个学期必须选修
numCourses 门课程,记为
0 到
numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
提示:
- 1 <=
numCourses<= 2000 - 0 <=
prerequisites.length<= 5000 prerequisites[i].length== 2- 0 <=
ai, bi<numCourses prerequisites[i]中的所有课程对 互不相同!!!

拓扑排序不用区分什么广度优先深度优先把自己弄乱了,抓住节点入度和出度的本质特征。
方法一: BFS从入度思考(从前往后排序), 入度为0的节点在拓扑排序中一定排在前面, 然后删除和该节点对应的边, 迭代寻找入度为0的节点。
方法二: DFS从出度思考(从后往前排序), 出度为0的节点在拓扑排序中一定排在后面, 然后删除和该节点对应的边, 迭代寻找出度为0的节点。
题解1 BFS(拓扑图模板)
class Solution {
vector<vector<int>> edges;
vector<int> indeg;
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
edges.resize(numCourses);
indeg.resize(numCourses);
const int m = prerequisites.size();
for(const auto& x : prerequisites){
// a->b:修b先修a
// 对应关系就是 修x[0]先修x[1]
// 所以是 x[1]->x[0]
// x[1]出度++, x[0]入度++
// 起点找边,终点找入度
edges[x[1]].push_back(x[0]);
// 入度(箭头指向的位置)
++ indeg[x[0]];
}
queue<int> q;
for(int i = 0; i < numCourses; i++){
// 可以直接修的课程,作为第一轮
if(! indeg[i])
q.push(i);
}
int visited = 0;
while(!q.empty()){
visited ++;
int u = q.front();
q.pop();
for(int v : edges[u]){
indeg[v] --;
if(! indeg[v])
// 下一轮
q.push(v);
}
}
return visited == numCourses;
}
};
题解2 DFS
class Solution {
vector<vector<int>> edges;
vector<int> visited;
bool valid = true;
public:
// 只需要判断是否存在一种拓扑排序,栈的作用仅仅是存放最终的拓扑排序结果
// 因此我们可以只记录每个节点的状态,而省去对应的栈。
void dfs(int u){
visited[u] = 1;
for(int& v : edges[u]){
if(! visited[v]){
dfs(v);
if(! valid)
return;
}
// 还没查完u呢,v就在搜索中了,不合法
// 相当于图里存在环
else if(visited[v] == 1){
valid = false;
return;
}
}
visited[u] = 2;
}
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
edges.resize(numCourses);
// 0:未搜索,1:正在搜索(找相邻结点),2:搜索完成
visited.resize(numCourses, 0);
const int m = prerequisites.size();
for(const auto& x : prerequisites){
edges[x[1]].push_back(x[0]);
}
for(int i = 0; i < numCourses && valid; i++){
if(! visited[i])
dfs(i);
}
return valid;
}
};