1. 题目链接:1863. 找出所有子集的异或总和再求和
2. 题目描述:
一个数组的 异或总和 定义为数组中所有元素按位
XOR的结果;如果数组为 空 ,则异或总和为0。
- 例如,数组
[2,5,6]的 异或总和 为2 XOR 5 XOR 6 = 1。给你一个数组
nums,请你求出nums中每个 子集 的 异或总和 ,计算并返回这些值相加之 和 。**注意:**在本题中,元素 相同 的不同子集应 多次 计数。
数组
a是数组b的一个 子集 的前提条件是:从b删除几个(也可能不删除)元素能够得到a。示例 1:
输入:nums = [1,3] 输出:6 解释:[1,3] 共有 4 个子集: - 空子集的异或总和是 0 。 - [1] 的异或总和为 1 。 - [3] 的异或总和为 3 。 - [1,3] 的异或总和为 1 XOR 3 = 2 。 0 + 1 + 3 + 2 = 6示例 2:
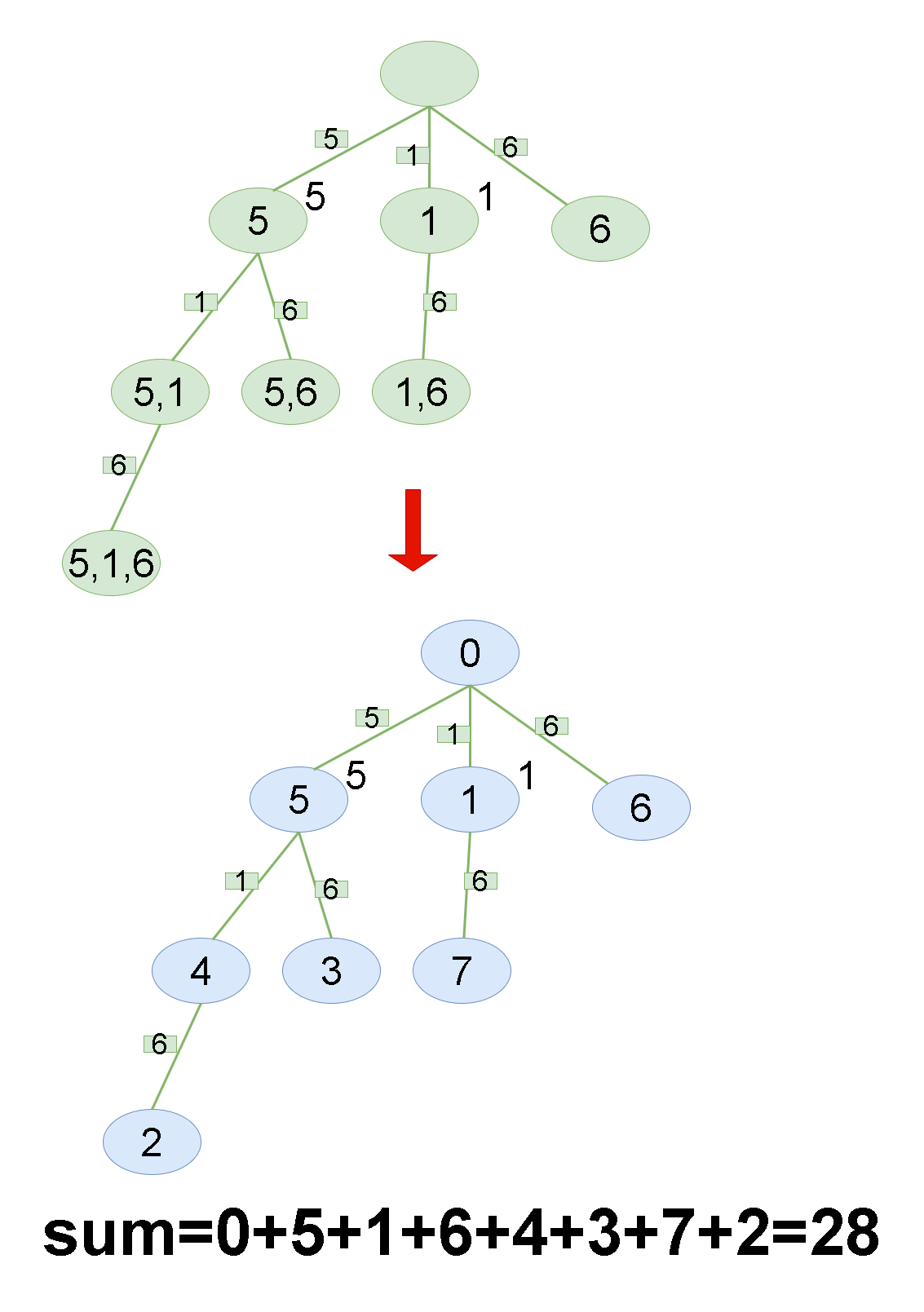
输入:nums = [5,1,6] 输出:28 解释:[5,1,6] 共有 8 个子集: - 空子集的异或总和是 0 。 - [5] 的异或总和为 5 。 - [1] 的异或总和为 1 。 - [6] 的异或总和为 6 。 - [5,1] 的异或总和为 5 XOR 1 = 4 。 - [5,6] 的异或总和为 5 XOR 6 = 3 。 - [1,6] 的异或总和为 1 XOR 6 = 7 。 - [5,1,6] 的异或总和为 5 XOR 1 XOR 6 = 2 。 0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28示例 3:
输入:nums = [3,4,5,6,7,8] 输出:480 解释:每个子集的全部异或总和值之和为 480 。提示:
1 <= nums.length <= 121 <= nums[i] <= 20
3. 解法(递归)
算法思路:
所有子集可以解释为:每个元素选择在或不在一个集合中(因此,子集有2^n个)。
- 定义两个变量
path和sum,分别表示当前子集的异或和以及所有子集的异或和之和。 - 在
subsetXORSum函数中,调用dfs函数进行深度优先搜索。传入参数为输入数组nums和起始位置0。 dfs函数是一个递归函数,用于遍历数组的所有子集并计算它们的异或和。- 在
dfs函数中,首先将当前子集的异或和path加入总和sum中。 - 然后,使用一个循环从当前位置
pos开始遍历数组中的每个元素。 - 在循环中,对当前元素进行异或操作,更新当前子集的异或和
path。 - 接着,递归调用
dfs函数,传入下一个位置i + 1作为起始位置。 - 递归返回后,执行回溯操作,恢复当前子集的异或和
path。 - 最后,当所有子集都被遍历完毕后,返回所有子集的异或和之和
sum。
通过这种深度优先搜索的方式,可以遍历数组的所有子集,并计算它们的异或和之和。
C++算法代码:
class Solution {
int path; // 当前子集的异或和
int sum; // 所有子集的异或和之和
public:
int subsetXORSum(vector<int>& nums) {
dfs(nums, 0); // 从第一个元素开始进行深度优先搜索
return sum; // 返回所有子集的异或和之和
}
void dfs(vector<int>& nums, int pos) {
sum += path; // 将当前子集的异或和加入总和中
for (int i = pos; i < nums.size(); i++) {
path ^= nums[i]; // 对当前元素进行异或操作,更新当前子集的异或和
dfs(nums, i + 1); // 继续递归搜索下一个元素
path ^= nums[i]; // 回溯,恢复当前子集的异或和
}
}
};