练习

1.Problem - 1A - Codeforces

AC代码:

#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
int n,m,a;
void solve() {
    cin>>n>>m>>a;
    cout<<(n/a+(n%a!=0))*(m/a+(m%a!=0))<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
//    cin>>t;
    while (t--) {
        solve();
    }
    return 0;
}

2.Problem - 118A - Codeforces

AC代码:

#include <bits/stdc++.h>
#define endl '\n'
using namespace std;
void solve() {
    string s;
    cin>>s;
    int n=s.size();
    for(int i=0;i<n;i++){
        if(s[i]>='A'&&s[i]<='Z') s[i]=(char)(s[i]-'A'+'a');
    }
    for(int i=-1;i<n-1;i++){
        if(s[i+1]=='a'||s[i+1]=='e'||s[i+1]=='i'||s[i+1]=='o'||s[i+1]=='u'||s[i+1]=='y'){
            continue;
        }
        else{
            cout<<'.'<<s[i+1];
        }
    }
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
//    cin>>t;
    while (t--) {
        solve();
    }
    return 0;
}

3.Problem - B - Codeforces（constructive algorithms）

这题看到字符串的头一定是0，尾一定是1，然后如果某段区间的头尾一样，那么可以将整段区间变得和头尾一样

直觉是一定得是有0和1紧挨着，才是yes，如下：

01

01

011111 011111

000011 000011

000001 000001

011001 011001

AC代码:

#include <bits/stdc++.h>
#define endl '\n'
using namespace std;
void solve() {
    string a,b;
    cin>>a>>b;
    int n=a.size();
    bool ok=false;
    for(int i=1;i<n;i++){
        if(a[i-1]=='0'&&b[i-1]=='0'&&a[i]=='1'&&b[i]=='1') ok=true;
    }
    if(ok) cout<<"Yes"<<endl;
    else cout<<"No"<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    cin>>t;
    while (t--) {
        solve();
    }
    return 0;
}

4.Problem - 1859B - Codeforces（constructive algorithms）

读题一定要慢，题目读错了想破脑袋也想不出来，血泪教训啊

题目是说可以从每个数组找一个整数移到另一个数组中去，首先由于只有最小值决定一个数组的值，所以肯定移最小值，移掉最小值，那么该数组的值就是次小值的值了，如果我们不作任何操作，那么每个数组的值都是最小值，我们自然希望操作之后次小值越多越好，但是我们取不到所有的次小值，至少舍弃一个，所以我们决定把其它所有最小值全都移到一个数组中，那么该数组的最小值就是全部的最小值，然后该次小值就被舍弃了，所以答案即为所有的次小值之和加上所有数的最小值再减去该数组的次小值，很明显，舍弃次小值最小的那个

AC代码:

#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=2e5+10;
int n;
void solve() {
    cin>>n;
    int sum=0;
    int min1,min2;
    int x=2e9,y=2e9;
    for(int i=0;i<n;i++){
        min1=min2=2e9;
        int m;
        cin>>m;
        for(int j=0;j<m;j++){
            int x;
            cin>>x;
            if(min1>=x) min2=min1,min1=x;
            else if(min2>x) min2=x;
        }
        x=min(x,min1);
        y=min(y,min2);
        sum+=min2;
    }
    cout<<sum+x-y<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    cin>>t;
    while (t--) {
        solve();
    }
    return 0;
}

5.Problem - 1858C - Codeforces（constructive algorithms）

构造题，构造序列

想到两个数a和b（a小于b），那么它们的最大公因数最大是a，所以从对于每个奇数，一直乘2，如果在合法范围内，那么就依次放在序列中，然后每次开头都是个奇数，加2即可

最后有一个小细节，就是vis数组开了N，但是判断了vis[a[cnt]*2]导致数组越界，出现RE错误

AC代码:

#include <bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=1e5+10;
int a[N];
bool vis[N];
int n;
void solve() {
    cin>>n;
    for(int i=1;i<=n;i++) vis[i]=true;
    int cnt=2;
    a[1]=1;
    a[2]=2;
    int x=1;
    while(cnt<n){
        while(a[cnt]*2<=n&&vis[a[cnt]*2]){
            cnt++;
            a[cnt]=a[cnt-1]*2;
            vis[a[cnt-1]*2]=false;
        }
        if(cnt<n){
            cnt++;
            x+=2;
            a[cnt]=x;
        }
    }
    for(int i=1;i<=n;i++) cout<<a[i]<<' ';
    cout<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    cin>>t;
    while (t--) {
        solve();
    }
    return 0;
}

6.Problem - 1851C - Codeforces

这题想到解法并不困难，主要就是可能会考虑不全

考虑从第一个开始枚举和第一个相同的，使得个数等于k，枚举到第k个时的位置记为a，从最后一个往前枚举和最后一个相同的，使得个数等于k，枚举到第k个时的位置记为b，如果a小于b，那么就可以分为两个block

但是没有特判第一个和最后一个相同的情况，要单独判断的原因是这种情况分为一个block，只要相同的个数大于等于k即可

AC代码：

#include <bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N = 2e5 + 10;
int c[N];
int k, n;
void solve() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) cin >> c[i];
    int a = -1, b = -1;
    int cnt = 0;
    if (c[1] == c[n]) {
        for (int i = 1; i <= n; i++) {
            if (c[i] == c[1]) cnt++;
        }
        if (cnt >= k) cout << "Yes" << endl;
        else cout<<"No"<<endl;
        return;
    }
    cnt=0;
    for (int i = 1; i <= n; i++) {
        if (c[i] == c[1]) {
            cnt++;
            if (cnt == k) {
                a = i;
                break;
            }
        }
    }
    cnt=0;
    for(int i=n;i>=1;i--){
        if(c[i]==c[n]){
            cnt++;
            if(cnt==k){
                b=i;
                break;
            }
        }
    }
    if (a != -1 && b != -1 && a < b) cout << "Yes" << endl;
    else cout << "No" << endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

7.Problem - 1849B - Codeforces

这题一开始想到了用优先队列写，自定义优先级，然后发现了一个问题，就是它的自定义的小于表示优先级小，刚好和sort里反过来

于是写了以下代码,但无奈超时

#include <bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=3e5+10;
struct node{
    int x;
    int idx;
    bool operator<(const node &W)const{
        if(x!=W.x) return x<W.x;
        return idx>W.idx;
    }
};
int n,k;
void solve() {
    cin>>n>>k;
    priority_queue<node>q;
    for(int i=1;i<=n;i++){
        int x;
        cin>>x;
        q.push({x,i});
    }
    while(q.size()){
        auto t=q.top();
        int x=t.x,idx=t.idx;
        q.pop();
        x-=k;
        if(x>0) q.push({x,idx});
        else {
            cout<<idx<<' ';
            break;
        }
    }
    while(q.size()){
        cout<<q.top().idx<<' ';
        q.pop();
    }
    cout<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

每次减的都是同一个值k，想到对k取模

该题解法为所有怪物的血量对k取模，如果为0，则设为k，然后按照血量从大到小的顺序就是被杀死的顺序

每次减的都是k，在血量大于k时，一个都没被杀死，一个顺序都确定不出来，所以我们把它们都变成只杀一次就会死的状态

AC代码:

#include <bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=3e5+10;
struct node{
    int x;
    int idx;
    bool operator<(const node &W)const{
        if(x!=W.x) return x<W.x;
        return idx>W.idx;
    }
};
int n,k;
void solve() {
    cin>>n>>k;
    priority_queue<node>q;
    for(int i=1;i<=n;i++){
        int x;
        cin>>x;
        x%=k;
        if(x==0) x=k;
        q.push({x,i});
    }
    while(q.size()){
        cout<<q.top().idx<<' ';
        q.pop();
    }
    cout<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

8.Problem - 1847B - Codeforces

思路一开始大体就是对的，就是代码实现上一直出问题

如果全部与起来为0，那么从头到尾一直与，变为0则成为一组，如果最后一组不为0的话，那么就合并到前一组

还有一个注意点是a&a=a

AC代码：

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=2e5+10;
int a[N];
int n;
void solve() {
    cin>>n;
    for(int i=0;i<n;i++) cin>>a[i];
    int sum=a[0]; 
    for(int i=1;i<n;i++) sum&=a[i];
    if(sum){
        cout<<1<<endl;
        return;
    }
    int x=a[0];
    int ans=0;
    for(int i=1;i<=n;i++){
        x&=a[i-1];
        if(x==0) {
            ans++;

            x=a[i];
        }
    }
    cout<<ans<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

9.Problem - 1844B - Codeforces（constructive algorithms）

这题一开始毫无思路

这题的突破口在于MEX，如果子序列中没有1的话，那么MEX值为1，所以我们使得包含1的子序列越多越好，个数用乘法原理算，往左包含1的长度乘往右包含1的长度，所以最佳策略是将1放在最中间

然后在这些包含1的子序列中，我们可以使得它们产生的质数全部为2或3，使得2和3在子序列中不出现，只需将2和3放在头和尾即可，这样包含1的序列除了整个序列产生不了质数，其它均可

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=2e5+10;
int a[N];
int n;
void solve() {
    cin>>n;
    if(n==1){
        cout<<1<<endl;
        return;
    }
    if(n==2){
        cout<<1<<' '<<2<<endl;
        return;
    }
    int mid=(n+1)/2;
    a[mid]=1;
    a[1]=2;
    a[n]=3;
    int cnt=3;
    for(int i=2;i<=mid-1;i++) a[i]=++cnt;
    for(int i=mid+1;i<=n-1;i++) a[i]=++cnt;
    for(int i=1;i<=n;i++) cout<<a[i]<<' ';
    cout<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

10.Problem - 1841B - Codeforces

就是先升序，然后最多降一次序，保证降的那次序的那个数比小于等于第一个数，再升序，保证数要小于等于第一个数

有很多判断条件，然后判断的优先顺序要理清楚

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
int q;
void solve() {
    cin>>q;
    vector<int>ans;
    bool ok=false;//ok为true表示已经降过一次了
    int x;
    cin>>x;
    ans.push_back(x);
    cout<<1;
    for(int i=1;i<q;i++){
        int x;
        cin>>x;
        if(!ok&&x<ans[ans.size()-1]&&x>ans[0]) cout<<0;//第一次降序但是比第一个数还大
        else if(ok&&x<ans[ans.size()-1]) cout<<0;//降过序了还降
        else if(ok&&x>ans[0]) cout<<0;//降过序了然后非降序但是比第一个数大
        else ans.push_back(x),cout<<1;
        if(ans.size()>=2&&ans[ans.size()-1]<ans[ans.size()-2]) ok=true;//表示降过一次了
    }
    cout<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

11.Problem - 1840C - Codeforces

从头到尾遍历，将连续一段的满足小于等于q的个数记录下来，如果个数大于等于k那么就对答案有贡献

假设一段的个数为n，那么贡献为n-x+1，x从k到n，作积分，所以为1+2+...+n-k+1=(n-k+2)*(n-k+1)/2

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=2e5+10;
int a[N];
int n,k,q;
void solve() {
    cin>>n>>k>>q;
    for(int i=1;i<=n;i++) cin>>a[i];
    vector<int>ans;
    int cnt=0;
    for(int i=1;i<=n;i++){
        if(a[i]<=q) cnt++;
        else{
            if(cnt>=k) ans.push_back(cnt);
            cnt=0;
        }
    }
    if(cnt>=k) ans.push_back(cnt);
    int res=0;
    for(auto v:ans){
        res+=(v-k+2)*(v-k+1)/2;
    }
    cout<<res<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

12.Problem - 1837C - Codeforces（constructive algorithms）

对问号进行填充，填充为0或1使得其通过翻转字串变成非降序的次数最少

我们可以先把1全部放在一起，把0全部放在一起，然后最后再翻转一次，所以我们的目标就是尽可能使得0挨在一起，1挨在一起

看问号两边，如果一样，则中间全部填一样的，如果不一样，那么就选择一边进行填充

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
string s;
void solve() {
    cin>>s;
    for(int i=0;i<(int)s.size();i++){
        if(s[i]=='?'){
            int l=i,r=i;
            while(s[l]=='?'&&l>0) l--;
            while(s[r]=='?'&&r<(int)s.size()-1) r++;
            if(s[l]=='?'&&s[r]!='?'){
                for(int j=l;j<=r-1;j++) s[j]=s[r];
                i=r;
            }
            else if(s[l]=='?'&&s[r]=='?'){
                for(int j=l;j<=r;j++) s[j]='0';
                i=r;
            }
            else if(s[r]=='?'&&s[l]!='?'){
                for(int j=l+1;j<=r;j++) s[j]=s[l];
                i=r;
            }
            else if(s[l]==s[r]){
                for(int j=l;j<=r-1;j++) s[j]=s[r];
                i=r;
            }
            else if(i!=(int)s.size()-1){
                for(int j=l+1;j<=r-1;j++) s[j]=s[l];
                i=r;
            }
            else{
                for(int j=l+1;j<=r-1;j++) s[j]=s[r];
                i=r;
            }
        }
    }
    for(int i=0;i<(int)s.size();i++) cout<<s[i];
    cout<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

13.Problem - 1834B - Codeforces

先在字符串长度短的前面补前导0

先看第一位，如果第一位不一样的话，假设第一个字符串的第二位为x，第二个字符串的第二位为y，那么第一个字符串的第二位可以取x到9，然后第二个字符串的第二位可以取0到y，为使差的绝对值最大，那么第一个字符串的第二位取9，第二个字符串的第二位取0，如果第一位一样的话，那么就直接是差的绝对值

以此类推

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=2E5+10;
int x[N];
string a,b;
void solve() {
    cin>>a>>b;
    int lena=a.size();
    int lenb=b.size();
    for(int i=0;i<lenb-lena;i++) a='0'+a;
    if(a[0]==b[0]) x[0]=0;
    else x[0]=abs(a[0]-b[0]);
    for(int i=1;i<lenb;i++){
        if(x[i-1]==0) x[i]=abs(a[i]-b[i]);
        else x[i]=9;
    }
    int ans=0;
    for(int i=0;i<lenb;i++) ans+=x[i];
    cout<<ans<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

14.Problem - 1831B - Codeforces

一开始用的双指针，如果相等然后就放在一起，但是以下样例说明此法不可行

6

2 2 1 2 2 1

1 2 1 2 2 2

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=4e5+10;
int a[N],b[N];
int c[N];
int n;
void solve() {
    cin>>n;
    for(int i=0;i<n;i++) cin>>a[i];
    for(int i=0;i<n;i++) cin>>b[i];
    int l=0,r=0,cnt=0;
    c[cnt++]=a[l];
    l++;
    while(l<n&&r<n){
        if(a[l]==c[cnt-1]) {
            c[cnt++]=a[l];
            l++;
        }
        else {
            c[cnt++]=b[r];
            r++;
        }
    }
    while(l<n) {
        c[cnt++]=a[l];
        l++;
    }
    while(r<n) {
        c[cnt++]=b[r];
        r++;
    }
    int ans=0;
    int sum=1;
    for(int i=1;i<cnt;i++){
        if(c[i]==c[i-1]) sum++;
        else{
            ans=max(ans,sum);
            sum=1;
        }
    }
    ans=max(ans,sum);
    cout<<ans<<endl;
    for(int i=0;i<cnt;i++) cout<<c[i]<<' ';
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
//    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

然后又想到搜连通块，以下样例说明此法不可行

5

1 2 2 2 2

2 1 1 1 1

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=2e5+10;
int a[N][2];
bool vis[N][2];
int n;
int ans;
int dx[4]={0,-1,0,1},dy[4]={1,0,-1,0};
void dfs(int x,int y,int num){
    ans=max(ans,num);
    vis[x][y]=true;
    for(int i=0;i<4;i++){
        int tx=x+dx[i],ty=y+dy[i];
       if(tx>=0&&tx<n&&ty>=0&&ty<=1&&a[tx][ty]==a[x][y]&&!vis[tx][ty]) dfs(tx,ty,num+1);
    }
}
void solve() {
    cin>>n;
    for(int i=0;i<n;i++) cin>>a[i][0];
    for(int i=0;i<n;i++) cin>>a[i][1];
    for(int i=0;i<n;i++){
        for(int j=0;j<2;j++){
            if(!vis[i][j]) dfs(i,j,1);
        }
    }
    cout<<ans<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
//    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

这题的关键在于我们可以任意取a数组连续的一段和b数组连续的一段组合起来，因为只要我们把它们前面的都先拿走即可

所以只需要统计出数组a和b每段连续相同数字的最大长度，然后对于a，b每个数字统计出的答案求和求最大值即可

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=4e5+10;
int a[N],b[N];
int n;
void solve() {
    cin>>n;
    map<int,int>mp1,mp2;
    for(int i=0;i<n;i++) cin>>a[i];
    for(int i=0;i<n;i++) cin>>b[i];
    int sum=1;
    for(int i=1;i<n;i++){
        if(a[i]==a[i-1]) sum++;
        else{
            mp1[a[i-1]]=max(mp1[a[i-1]],sum);
            sum=1;
        }
    }
    if(sum) mp1[a[n-1]]=max(mp1[a[n-1]],sum);
    sum=1;
    for(int i=0;i<n;i++){
        if(b[i]==b[i-1]) sum++;
        else{
            mp2[b[i-1]]=max(mp2[b[i-1]],sum);
            sum=1;
        }
    }
    if(sum) mp2[b[n-1]]=max(mp2[b[n-1]],sum);
    int ans=0;
    for(auto v:mp1){
        ans=max(ans,v.second+mp2[v.first]);
    }
    for(auto v:mp2){
        ans=max(ans,v.second+mp1[v.first]);
    }
    cout<<ans<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

15.Problem - 1829D - Codeforces

递归

对于x分成x/3和x/3*2，一直递归下去，看能否得到m

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
int n,m;
bool ok;
void f(int x){
    if(x==m){
        ok=true;
        return;
    }
    if(x%3==0){
        int a=x/3,b=x/3*2;
        if(a==m||b==m){
            ok=true;
            return;
        }
        if(a>m) f(a);
        if(b>m) f(b);
    }
}
void solve() {
    cin>>n>>m;
    ok=false;
    f(n);
    if(ok) cout<<"Yes"<<endl;
    else cout<<"No"<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

16.Problem - 1825B - Codeforces

特判n等于1和m等于1的情况

不妨设n小于m，如果n大于m，只要swap一下就行

在1，2，3位置分别放置数，使得蓝色区域diff最大，紫色区域diff次大

diff最大和次大无非两种情况：

1.最大减最小，最大减次小

2.最大减最小，次大减最小

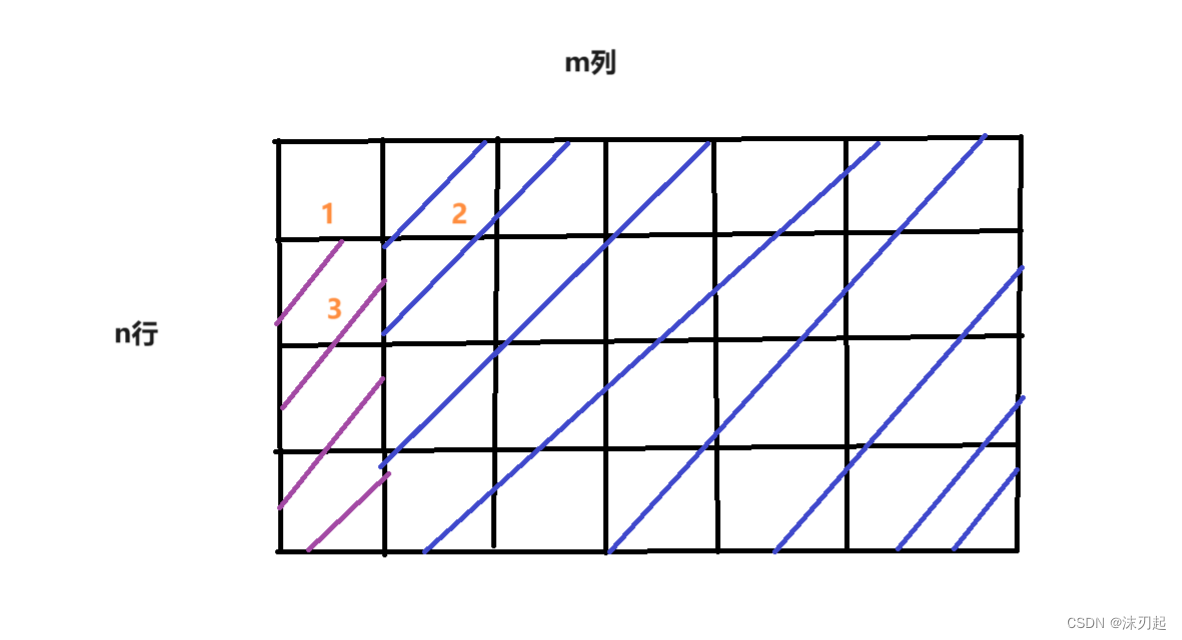
AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
int n,m;
void solve() {
    cin>>n>>m;
    int max1=-2e9,max2=-2e9;
    int min1=2e9,min2=2e9;
    for(int i=1;i<=n*m;i++){
        int x;
        cin>>x;
        if(max1<=x) max2=max1,max1=x;
        else if(max2<x) max2=x;
        if(min1>=x) min2=min1,min1=x;
        else if(min2>x) min2=x;
    }
    if(n==1){
        int diff=max1-min1;
        cout<<(m-1)*diff<<endl;
    }
    if(m==1){
        int diff=max1-min1;
        cout<<(n-1)*diff<<endl;
        return;
    }
    if(n>m) swap(n,m);//n小m大
    int diff1=max1-min1,diff2=max1-min2;
    int ans1=n*(m-1)*diff1+(n-1)*diff2;
    int diff3=max1-min1,diff4=max2-min1;
    int ans2=n*(m-1)*diff3+(n-1)*diff4;
    cout<<max(ans1,ans2)<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

17.Problem - 1816B - Codeforces（constructive algorithms）

第一个是要加的，最后一个也是要加的，然后和第一个隔奇数个位置的就是要减的

通过观察第三个样例，发现可以如下构造：

第一个数和最后一个数放最大的和次大的

然后斜着10，9，8,7,

再重新斜着6，5，4，3，2，1

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int n;
void solve() {
    cin>>n;
    a[1]=2*n-1;
    b[n]=2*n;
    int cnt=2*n-1;
    for(int i=2;i<=n-2;i+=2){
        b[i]=--cnt;
        a[i+1]=--cnt;
    }
    for(int i=1;i<=n-1;i+=2){
        b[i]=--cnt;
        a[i+1]=--cnt;
    }
    for(int i=1;i<=n;i++) cout<<a[i]<<' ';
    cout<<endl;
    for(int i=1;i<=n;i++) cout<<b[i]<<' ';
    cout<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

18.Problem - 1811B - Codeforces

由于传送带上移动是不会消耗精力的，所以统一都把它们放在同一块区域，把整个正方形横一刀竖一刀平均分成四块

然后把起点和终点通过传送带送到左上角那块区域

然后和（n/2,n/2）这个点进行比较，判断是第几层，最后算出相差几层即可

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
int n;
int x,y;
int a,b;
void solve() {
    cin>>n>>x>>y>>a>>b;
    x=min(x,n+1-x);
    y=min(y,n+1-y);
    a=min(a,n+1-a);
    b=min(b,n+1-b);
    int ans1=max(abs(n/2-x),abs(n/2-y));
    int ans2=max(abs(n/2-a),abs(n/2-b));
//    cout<<x<<' '<<y<<' '<<ans1<<endl;
//    cout<<a<<' '<<b<<' '<<ans2<<endl;
    cout<<abs(ans1-ans2)<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

19.Problem - 1809B - Codeforces

sqrt有精度问题，可能会向上取整，因此在判断是否是平方数时，写判断条件x*x大于等于n

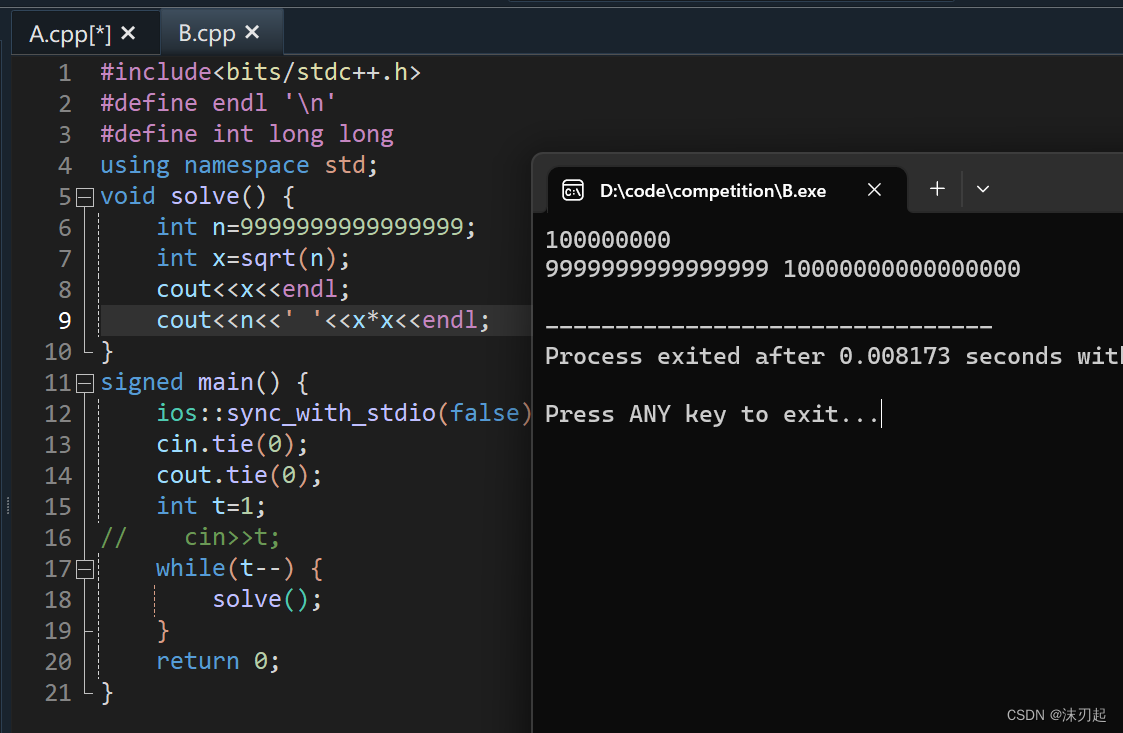
无非两种情况，黑色的和红色的

列表:

1 4 9 12 25

0 1 2 3 4

得出结论，当n为平方数时，答案为sqrt(n)否则答案为sqrt(n)-1

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
int n;
void solve() {
    cin>>n;
    int x=sqrt(n);
    if(x*x>=n) cout<<x-1<<endl;
    else cout<<x<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

-----------------------------------------------------------分割线-------------------------------------------------------------

检验水平（连续5题）（做完一组然后总结）

第一组：

1.Problem - 1804B - Codeforces（implementation）

模拟+贪心

如果改包疫苗过期了或者用完了，那么就重新开一包

然后重新开一包疫苗的时刻在满足下一个病人能用上的基础上越晚越好

做这题不是很顺利，思路理的不是很清楚

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=2e5+10;
int t[N];
int n,k,d,w;
void solve() {
    cin>>n>>k>>d>>w;
    for(int i=1;i<=n;i++) cin>>t[i];
    int ans=1;//用了几包疫苗
    int st=t[1]+w;//该包疫苗开始用的时刻
    int cnt=0;//改包疫苗用了几支
    for(int i=1;i<=n;i++){
        if(t[i]-st>d||cnt==k){
            ans++;
            st=t[i]+w;
            cnt=0;
        }
        cnt++;
    }
    cout<<ans<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

2.Problem - 1802B - Codeforces（implementation）

虽然最后独立做出了，但是中间的过程非常不顺利

首先题意一开始就理解的不准确，题目所说的是对于任意一个时刻都得满足要求

我们会发现，每3个就至少有1组性别一样，每5个就至少有2组性别一样，得到的结论是x个，则至少有(x-1)/2组性别一样，那么总共需要(x-1)/2+x-(x-1)/2*2个鸟笼（这里注意乘2的位置，要写在后面而不能写在前面）

由于是对于每一个时刻，所以比如说下一天医生来检查，但是该天有一些鸟的性别仍然是未知的，这也是需要考虑的，有几只鸟性别未知，就直接加几个鸟笼即可

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=2e5+10;
int b[N];
int n;
int res1,res2;
void solve() {
    cin>>n;
    for(int i=1;i<=n;i++) cin>>b[i];
    int sum=0;
    int cnt=0;
    int ans=0;
    for(int i=1;i<=n;i++){
        if(b[i]==1) cnt++;
        else{
            res1=(sum-1)/2+sum-(sum-1)/2*2;
            res2=(sum+cnt-1)/2+sum+cnt-(sum+cnt-1)/2*2;
            ans=max(ans,max(res1+cnt,res2));
            sum+=cnt;
            cnt=0;
        }
    }
    if(cnt){
        res1=(sum-1)/2+sum-(sum-1)/2*2;
        res2=(sum+cnt-1)/2+sum+cnt-(sum+cnt-1)/2*2;
        ans=max(ans,max(res1+cnt,res2));
    }
    cout<<ans<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

3.Problem - 1800C1 - Codeforces

很快想到思路并AC

遇到0就加上前面最大的，想到用大根堆，遇到0就加上队头

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=5010;
int s[N];
int n;
void solve() {
    cin>>n;
    for(int i=1;i<=n;i++) cin>>s[i];
    priority_queue<int>q;
    int ans=0;
    for(int i=1;i<=n;i++){
        if(s[i]) q.push(s[i]);
        else if(q.size()){
            ans+=q.top();
            q.pop();
        }
    }
    cout<<ans<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

4.Problem - 1800B - Codeforces

做题过程还算顺利，关键在于用map记录字母的个数

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
int n,k;
string s;
void solve() {
    cin>>n>>k;
    cin>>s;
    map<int,int>mp;
    for(int i=0;i<(int)s.size();i++) mp[s[i]]++;
    int ans=0;
    for(int i='a';i<='z';i++){
        if(mp[i]<mp[i-32]) swap(mp[i],mp[i-32]);
        ans+=mp[i-32];
        mp[i]-=mp[i-32];
        mp[i-32]=0;
    }
    int sum=0;
    for(int i='a';i<='z';i++) sum+=mp[i]/2;
    ans+=min(sum,k);
    cout<<ans<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

5.Problem - 1798B - Codeforces

思路想的还是很快的，然后后面也对了，只不过一开始输入的时候卡死了，就是如果开二维数组会爆空间，所以需要动态数组，想到用vector，然后没用push_back，直接用cin>>a[i][j]，然后输入就卡死了

该题的关键在于后面出现过的前面就不可能赢，那么就从后往前确定赢家，如果没出现过，那么就可以让他成为赢家，注意只能确定一个，因为他在前面不可能赢，所以对前面没有任何影响，然后将他们都标记为出现过，如果最后确定的赢家个数不为m，那么说明没有可行的方案

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=5e4+10;
int c[N];
bool flag[N];
int m;
void solve() {
    cin>>m;
    vector<vector<int>>a(m);
    for(int i=0;i<m;i++){
        cin>>c[i];
        for(int j=0;j<c[i];j++){
            int x;
            cin>>x;
            a[i].push_back(x);
        }
    }
    memset(flag,false,sizeof flag);
    vector<int>ans;
    for(int i=m-1;i>=0;i--){
        bool ok=false;
        for(int j=0;j<c[i];j++){
            if(!flag[a[i][j]]&&!ok) ans.push_back(a[i][j]),ok=true;
            flag[a[i][j]]=true;
        }
    }
    int len=ans.size();
    if(len!=m){
        cout<<-1<<endl;
        return;
    }
    for(int i=len-1;i>=0;i--) cout<<ans[i]<<' ';
    cout<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

总结：

1.最重要的是读题目，题意一定要理解准确，题意理解错了，怎么都不可能做对，切忌忽略某个单词或短语，每个单词都不能漏

读题的时候慢慢来，一点一点理解，不要想着一下子就读完，先看输入和输出，了解有哪些变量，然后再去看题面，然后看题面的时候就慢慢看，如果前一句没理解，就多读几遍，不能急着看下一句

然后最重要的就是看样例，在草稿纸上模拟样例，要准确的理解样例，每个样例都要模拟一遍，这样才算看完了题目

2.另外就是不要急着直接敲代码，要先在草稿纸上理清思路，然后做到快速地敲完代码，如果思路没理清，就坚决不写代码

3.注意一些输入卡死的问题，特别是在用vector代替二维数组的时候，用push_back就行了

第二组：

1.Problem - 1796B - Codeforces

交了一发就AC了

该题思路很简单，一种情况是a和b的第一个字符相等或者最后一个字符相等，另一种情况是连续两个字符相同

但是需要查找字符串，想到用string类的find函数，但是担心时间复杂度不够，虽然单次查找时间复杂度为O（n），但是需要多次查找，最差可能就O（m*n）了，担心会超时，但可能实际运行起来不会达到这么差的情况，然后顺利通过了

find的时间复杂度为O（n），n为文本串的长度，和kmp差不多

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
string a,b;
void solve() {
    cin>>a>>b;
    int lena=a.size();
    int lenb=b.size();
    if(a[0]==b[0]){
        cout<<"Yes"<<endl;
        cout<<a[0]<<'*'<<endl;
        return;
    }
    if(a[lena-1]==b[lenb-1]){
        cout<<"Yes"<<endl;
        cout<<'*'<<a[lena-1]<<endl;
        return;
    }
    for(int i=0;i<(int)a.size()-1;i++){
        string s="";
        s+=a[i];
        s+=a[i+1];
        int pos=b.find(s,0);
        if(pos>=0&&pos<(int)b.size()){
            cout<<"Yes"<<endl;
            cout<<'*'<<s<<'*'<<endl;
            return;
        }
    }
    cout<<"No"<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

2.Problem - 1791D - Codeforces

不要想到一个思路就急着敲代码，敲完代码发现思路错了就白忙活一场，在想到一个思路时，自己先再造一些样例来检验思路，样例越极端越刁钻越好，在这步做完之后确定没什么大问题，再去敲代码

一开始猜测是找到第一个在之前出现过的，在它的前面画分界线，然后没有自己再造一些样例来检验就急着敲代码了，最后发现思路有问题，代码也白敲了，比如abcaxxbcda

然后想到可以直接暴力，就是对于所有划分的情况取max

利用set的自动去重来求种数，利用map来计数每种字母的个数

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
int n;
string s;
void solve() {
    cin>>n;
    cin>>s;
    set<char>s1,s2;
    map<char,int>mp1,mp2;
    s1.insert(s[0]);
    mp1[s[0]]++;
    for(int i=1;i<n;i++) s2.insert(s[i]),mp2[s[i]]++;
    int ans=s1.size()+s2.size();
    for(int i=1;i<n-1;i++){
        s1.insert(s[i]),mp1[s[i]]++;
        mp2[s[i]]--;
        if(mp2[s[i]]==0) s2.erase(s[i]);
        ans=max(ans,(int)s1.size()+(int)s2.size());
    }
    cout<<ans<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

3.Problem - 1791D - Codeforces

这题思路挺简单的，通过观察样例发现，可以从后往前推，最后一列一共有两种数，数量多的是最后一个数，另一个是倒数第二个数，然后往前一列一列，没出现过的数依次是前一个数

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=110;
int a[N][N];
int n;
bool flag[N];
void solve() {
    cin>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<n-1;j++){
            cin>>a[i][j];
        }
    }
    memset(flag,false,sizeof flag);
    vector<int>ans;
    map<int,int>mp;
    for(int i=0;i<n;i++) mp[a[i][n-2]]++;
    int cnt=0;
    int x[2]={0};
    for(auto v:mp){
        x[cnt++]=v.first;
    }
    if(mp[x[0]]<mp[x[1]]) swap(x[0],x[1]);
    ans.push_back(x[0]);
    ans.push_back(x[1]);
    flag[x[0]]=flag[x[1]]=true;
    for(int i=n-2;i>=0;i--){
        for(int j=0;j<n;j++){
            if(!flag[a[j][i]]){
                ans.push_back(a[j][i]);
                flag[a[j][i]]=true;
                break;
            }
        }
    }
    int len=ans.size();
    for(int i=len-1;i>=0;i--) cout<<ans[i]<<' ';
    cout<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

4.Problem - 1784A - Codeforces（VK Cup 2022 - Финальный раунд (Engine)）

这题做的不是很顺利，虽然后面知道这题是要使得1，2，3，.....至少存在一个，但是无奈不知道咋写代码

可以利用multiset会自动升序但不会自动去重，让它们先排成一队

然后cnt从1开始自增，让multiset里的数一个一个变成cnt

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=2e5+10;
int a[N];
int n;
void solve() {
    multiset<int>s;
    cin>>n;
    for(int i=1;i<=n;i++){
        int x;
        cin>>x;
        s.insert(x);
    }
    int cnt=1;
    int ans=0;
    while(s.size()){
        while(s.size()&&*s.begin()<cnt) s.erase(s.begin());
        if(s.empty()) break;
        ans+=(*s.begin()-cnt);
        s.erase(s.begin());
        cnt++;
    }
    cout<<ans<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

5.Problem - 1781B - Codeforces（VK Cup 2022 - Отборочный раунд (Engine)）

不太会做，没啥思路

这两句话翻译一下就是当除第i个人本身之外，至少去了ai个人的话，那么第i个人必须去

我们从题目条件出发，得到确定的信息，然后由此作为基础开始推导

首先，如果大的都能满足的话，那么小的一定能满足，我们对数组a进行升序，从头遍历，如果当前必须选就继续遍历，直到不是必须选，那么选择当前遍历过的数，其它数不选就是一种可行的方案

然后我们继续往后选择，一开始的话可能满足不了，但是当到某个数能满足的时候，那么前面这些选择的不能满足的数也能满足了，因为至少去了ai个人的话，那么第i个人必须去，后面的数大，都得去的话，那么前面更得去了

如此循环

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=2e5+10;
int a[N];
int n;
void solve() {
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    a[n+1]=-1;
    sort(a+1,a+1+n);
    int ans=0;
    int cnt=0;
    for(int i=1;i<=n;){
        while(a[i]<=cnt){
            cnt++;
            i++;
        }
        ans++;
        while(a[i]>cnt){
            cnt++;
            i++;
        }
    }
    cout<<ans<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

总结：

1.有时候最快时间复杂度可能会超时，但是实际上平均运行起来不一定会超时

2.不要想到一个思路就急着敲代码，敲完代码发现思路错了就白忙活一场，在想到一个思路时，自己先再造一些样例来检验思路，样例越极端越刁钻越好，在这步做完之后确定没什么大问题，再去敲代码

3.对于让某些数依次变成cnt自增（两边都要往下遍历），先让这些数按照从小到大的顺序排成一排，可以放入multiset中，利用while(s.size()) s.erase(s.begin())，将这些数依次变成cnt自增

4.如果感觉没啥思路，无从下手，感觉很绕，那么就仔细读题目，从题目中寻找确定的信息，在此基础上进行推导，一步一步推出确定的信息

第三组：

1.Problem - 1772C - Codeforces

该题也是比较简单，就是从1开始，然后增1，增2，...，就是一开始忘记了数组a要严格递增这一条件，wa了一发，然后立马就改了过来，保证后面可以加1然后到n

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
int k,n;
void solve() {
    cin>>k>>n;
    vector<int>ans;
    int x=1;
    int diff=1;
    ans.push_back(x);
    for(int i=2;i<=k;i++){
        x+=diff;
        x=min(x,n-(k-i));
        ans.push_back(x);
        diff++;
    }
    for(auto v:ans) cout<<v<<' ';
    cout<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

2.Problem - 1770B - Codeforces

这题感觉也还好

要使得连续k个数的max+min的最大值最小，那么得平均一下，最大值肯定要和最小值相配，次大值和次小值相配

所以直接构造序列使得最大和最小相邻，次大和次小相邻，以此类推

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=2e5+10;
int a[N];
int k,n;
void solve() {
    cin>>n>>k;
    vector<int>ans;
    for(int i=1;i<=n;i++) a[i]=i;
    for(int i=1,j=n;i<=j;i++,j--){
        ans.push_back(a[j]);
        if(a[i]!=a[j]) ans.push_back(a[i]);
    }
    for(auto v:ans) cout<<v<<' ';
    cout<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

3.Problem - 1770A - Codeforces

这题一开始想的是数组b从大到小排序，数组a从小到大排序，然后数组b依次赋值给a，代码如下，不知道为什么错了

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=110;
int a[N];
int n,m;
void solve() {
    cin>>n>>m;
    multiset<int,greater<int>>s;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=m;i++){
        int x;
        cin>>x;
        s.insert(x);
    }
    sort(a+1,a+1+n);
    int idx=1;
    while(s.size()){
        if(*s.begin()>a[idx]) {
            a[idx]=*s.begin(),s.erase(s.begin());
            if(idx<=n) idx++;
        }
        else a[idx]=*s.begin(),s.erase(s.begin());
    }
    int ans=0;
    for(int i=1;i<=n;i++) ans+=a[i];
    cout<<ans<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

我们可以确定的是数组b的每个值一定是要赋值给a的，这是肯定的，所以我们每次都给最小的那个a就可以了

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=110;
int a[N];
int n,m;
void solve() {
    cin>>n>>m;
    priority_queue<int,vector<int>,greater<int>>q;
    for(int i=1;i<=n;i++){
        int x;
        cin>>x;
        q.push(x);
    }
    for(int i=1;i<=m;i++){
        int x;
        cin>>x;
        q.pop();
        q.push(x);
    }
    int ans=0;
    while(q.size()){
        int t=q.top();
        q.pop();
        ans+=t;
    }
    cout<<ans<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

4.Problem - 1766B - Codeforces

其实只要后面有两个连续字母在前面出现过，那么总操作次数就会小于n，所以问题就转换成了字符串的查找问题

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
int n;
string s;
void solve() {
    cin>>n;
    cin>>s;
    for(int i=0;i<(int)s.size()-1;i++){
        string str="";
        str+=s[i];
        str+=s[i+1];
        int pos=s.find(str,i+2);
        if(pos>=0&&pos<(int)s.size()-1){
            cout<<"Yes"<<endl;
            return;
        }
    }
    cout<<"No"<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

5.Problem - B1 - Codeforces

Копирование файлов I - 洛谷(洛谷，带中文翻译)

数据量比较小，因此直接暴力模拟即可

从小到大输出某一时刻两者进度相同的那个进度，然后每个进度只输出一次，那么当某个进度出现过就标记，下次就不输出了，其中0必输出，一开始就标记

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=110;
int a[N];
int n;
bool flag[N];
void solve() {
    cin>>n;
    int sum=0;
    for(int i=1;i<=n;i++) {
        cin>>a[i];
        sum+=a[i];
    }
    int sum1=0;
    cout<<0<<endl;
    flag[0]=true;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=a[i];j++){
            int x=100*j/a[i];
            int y=100*(sum1+j)/sum;
            if(x==y&&!flag[x]) cout<<x<<endl,flag[x]=true;
        }
        sum1+=a[i];
    }
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
//    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

总结：

1.我们得从繁琐的题目中抽取一定能够确定的信息，那种很妙的超级关键的信息，可能不是那么容易就能够从中抽离出来，需要通过多做这一类题来锻炼这一能力

2.当数据量比较小的时候，考虑暴力

第四组：

1.Problem - 1765M - Codeforces

独立做出

将n分解为a，b之和，然后使得a,b的最小公倍数最小

比如说8,可以分解为1+7，2+6，3+5，4+4，然后我们发现质数从小到大为2，3，5，7，...，如果n是某个质数x的倍数，那么就可以分解为n/x+n/x*(x-1)，这样它们的最小公倍数就是n/x*(x-1)，如果最后不是任何一个质数的倍数，就分解为1+(n-1)

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=2e5+10;
int prime[N];
bool st[N];
int n;
int cnt;
void get_prime(int n){
    for(int i=2;i<=n;i++){
        if(!st[i]) prime[cnt++]=i;
        for(int j=0;prime[j]<=n/i;j++){
            st[prime[j]*i]=true;
            if(i%prime[j]==0) break;
        }
    }
}
void solve() {
    cin>>n;
    for(int i=0;i<cnt;i++){
        if(n%prime[i]==0){
            cout<<n/prime[i]<<' '<<n/prime[i]*(prime[i]-1)<<endl;
            return;
        }
        if(prime[i]>n) break;
    }
    cout<<1<<' '<<n-1<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    get_prime(N);
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

2.Problem - 1765E - Codeforces

这题很简单

当a小于等于b的时候，我们直接n/a上取整

然后当a小于b的时候，我们就可以通过中间商赚差价（买卖次数不限），通过不断倒卖，理论上可以得到的银币无上限，所以只需要回答一个问题，得到一个金币即可

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
int n,a,b;
void solve() {
    cin>>n>>a>>b;
    if(a<=b) cout<<n/a+(n%a!=0)<<endl;
    else cout<<1<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

3.Problem - 1761B - Codeforces

wa了5发，错了然后看了错误样例，然后修正了思路

其实通过自己造样例，可以发现除了一种特殊情况，即121212一直间隔一个相等的这种情况，它的答案是n/2+1，因为每操作一次就删除2个，然后最后一个还要删除一次

其它情况都可以做到操作n次，比如12134，可以把后面的1先删掉，其它按顺序一个一个删即可

AC代码：

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=110;
int a[N];
int n;
void solve() {
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    if(n<=3){
        cout<<n<<endl;
        return;
    }
    bool ok=true;
    for(int i=1;i<=n-2;i++){
        if(a[i]!=a[i+2]) ok=false;
    }
    if(ok) cout<<n/2+1<<endl;
    else cout<<n<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

4.Problem - 1760D - Codeforces

上一题和这一题都是wa了好多发，真的是太急了，错了就看错误样例，然后再修正，这样有作弊之嫌，下次一定不能这样

还是应该先自己造样例，等确定思路没问题之后，再敲代码

这题其实不需要看山谷繁琐的定义，就看那形状就行，其实只有一种情况不满足，就是升过一次之后再降一次

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=2e5+10;
int a[N];
int n;
void solve() {
    cin>>n;
    for(int i=0;i<n;i++) cin>>a[i];
    bool ok=false;
    for(int i=1;i<n;i++){
        if(a[i]>a[i-1]&&!ok) ok=true;//升过一次
        if(a[i]<a[i-1]&&ok){//升过一次,降过一次
            cout<<"No"<<endl;
            return;
        }
    }
    cout<<"Yes"<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

5.Problem - 1744C - Codeforces

题意：当前红绿灯的颜色为c，问其往右遍历到最近的g的时间，在所有当前为颜色c的情况中取最大

由于会循环到开头，所以字符串重复加一遍

比如当前颜色为r，那我们找到第一个r，然后等到下一个 g时，求它们之间的距离即可，记录下来取max

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
int n;
char c;
string s;
void solve() {
    cin>>n>>c;
    cin>>s;
    s+=s;
    int okr=-1,oky=-1;
    int ansr=0,ansy=0;
    for(int i=0;i<n*2;i++){
        if(okr==-1&&s[i]=='r') okr=i;
        else if(oky==-1&&s[i]=='y') oky=i;
        else if(s[i]=='g'){
            if(okr!=-1) ansr=max(ansr,i-okr);
            if(oky!=-1) ansy=max(ansy,i-oky);
            okr=-1;
            oky=-1;
        }
    }
    if(c=='r') cout<<ansr<<endl;
    else if(c=='y') cout<<ansy<<endl;
    else cout<<0<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

总结：

1.不能错了就看错误样例，然后再修正，这样有作弊之嫌，下次一定不能这样

还是应该先自己造样例，等确定思路没问题之后，再敲代码

2.debug能力，学会输出找错，出问题了就把它们都输出一遍

第五组：

1.Problem - 1732A - Codeforces

感觉照自己之前的水平不太可能想到，但是现在确确实实是自己想出来的，而且还挺快，思维水平确实提高了不少

我们可以发现最多三次，因为相邻两个数一定是互质的，a[n]和n求最大公约数，a[n-1]和n-1求最大公约数，然后它们的最大公约数一定是1，这两个操作的代价之和是3

如果一开始所有数的最大公约数为1，那么代价为0

如果只要操作a[n]，那么代价为1

如果只要操作a[n-1]，那么代价为2

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=25;
int a[N],b[N];
int n;
int gcd(int a,int b){
    if(b==0) return a;
    return gcd(b,a%b);
}
void solve() {
    cin>>n;
    int x;
    cin>>x;
    int ans=x;
    for(int i=2;i<=n;i++) {
        cin>>a[i];
        ans=gcd(ans,a[i]);
    }
    if(ans==1) cout<<0<<endl;
    else if(gcd(ans,gcd(a[n],n))==1) cout<<1<<endl;
    else if(gcd(ans,gcd(a[n-1],n-1))==1) cout<<2<<endl;
    else cout<<3<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

2.Problem - 1725B - Codeforces

一开始还是太急了，样例错了又忍不住看错误样例了

然后后面静下心来不看错误样例了，然后自己造样例，然后慢慢的就AC了

从小到大排序，利用双指针，将大值和小值配对

AC代码：

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=1e5+10;
int p[N];
int n,d;
void solve() {
    cin>>n>>d;
    for(int i=1;i<=n;i++) cin>>p[i];
    sort(p+1,p+1+n);
    int ans=0;
    for(int i=1,j=n;i<=j;j--){
        int x=d/p[j]+1;
        if(x>=2) i+=x-2;
        if(i<j||(i==j&&x==1)) ans++;
        if(x>1) i++;
    }
    cout<<ans<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
//    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

3.Problem - 1721B - Codeforces

原本以为是一个简简单单的bfs，然后最后超时了，样例达1e4，超时是肯定的

#include<bits/stdc++.h>
#include<cmath>
#define endl '\n'
//#define int long long
using namespace std;
const int N=1010;
bool st[N][N];
int dx[4]={-1,1,0,0},dy[4]={0,0,1,-1};
int n,m,sx,sy,d;
struct node{
    int x,y,step;
};
void solve() {
    cin>>n>>m>>sx>>sy>>d;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            st[i][j]=false;
        }
    }
    queue<node>q;
    q.push({1,1,0});
    st[1][1]=true;
    while(q.size()){
        auto t=q.front();
        q.pop();
        int x=t.x,y=t.y,step=t.step;
        if(x==n&&y==m){
            cout<<step<<endl;
            return;
        }
        for(int i=0;i<4;i++){
            int tx=x+dx[i],ty=y+dy[i];
            if(tx<1||tx>n||ty<1||ty>m||abs(tx-sx)+abs(ty-sy)<=d||st[tx][ty]) continue;
            st[tx][ty]=true;
            q.push({tx,ty,step+1});
        }
    }
    cout<<-1<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

激光源主要发出一个十字架，十字架起主要截断作用

如果不走回头路，然后可以到达的话，步数一定是n+m-2（确实不会走回头路）

然后如果先右再下和先下再右这两条路被截断了，那么一定到达不了，否则就可以到达

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
int n,m,sx,sy,d;
void solve() {
    cin>>n>>m>>sx>>sy>>d;
    if((sx-d<=1&&sx+d>=n)||(sy-d<=1&&sy+d>=m)||(sx-d<=1&&sy-d<=1)||(sx+d>=n&&sy+d>=m)) cout<<-1<<endl;
    else cout<<n+m-2<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

4.Problem - 1715B - Codeforces

这题已经鸽了好几天了，之前有些思路但是一直没做对

今天又重新做这题，终于做对了

首先我们需要一个数min(k*b,k*(b+1)-1)来确保beauty，然后接下来就是补数，优先补k-1，然后不足k-1则把剩下的也补了，然后个数小于n则补0，如果个数大于n那么就构造不成功

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
int n,k,b,s;
void solve() {
    cin>>n>>k>>b>>s;
    int x=min(k*(b+1)-1,s);
    if(s<k*b){
        cout<<-1<<endl;
        return;
    }
    s-=x;
    if((k-1)*(n-1)<s){
        cout<<-1<<endl;
        return;
    }
    vector<int>ans;
    ans.push_back(x);
    while(s>k-1){
        if(s>k-1) ans.push_back(k-1),s-=k-1;
        if((int)ans.size()>n){
            cout<<-1<<endl;
            return;
        }
    }
    if(s) ans.push_back(s);
    if((int)ans.size()>n){
        cout<<-1<<endl;
        return;
    }
    while((int)ans.size()<n) ans.push_back(0);
    for(auto v:ans) cout<<v<<' ';
    cout<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

5.Problem - 1713B - Codeforces

我们可以发现，只要不是出现先降再升就是Yes，因为一旦出现这种情况，那么就不能连续对一段区间进行操作，需要分两半进行

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=1e5+10;
int a[N];
int n;
void solve() {
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];    
    bool ok=false;//是否降
    bool flag=false;//是否升
    for(int i=2;i<=n;i++){
        if(!ok&&a[i-1]>a[i]){
            ok=true;
        }
        else if(ok&&!flag&&a[i-1]<a[i]){
            flag=true;
        }
    }
    if(ok&&flag) cout<<"No"<<endl;
    else cout<<"Yes"<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

总结：

1.想到用dfs或者bfs时，得先看数据范围，那种大的离谱的肯定不能用dfs和bfs

2.对于起点和终点已知（终点在起点的右下方），如果只能向右和向下走，那么向右走的步数是一定的，向下走的步数也是一定的，总步数也是一定的

第六组：

1.Problem - 1704B - Codeforces

实在是没啥思路，主要是想一个一个的确定v的值，始终不能得到最优解

这题根据每个a[i]算出v的范围，记为[l,r]，枚举每个a[i]所需要的v的范围，如果和上一次确定的范围有交集，那么就取它们的交集作为新的范围，这样不断缩小范围，v只要在新的范围里取即可

然后如果和上一次的范围没有交集，那么就得换一个新的范围

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=2e5+10;
int a[N];
int n,x;
void solve() {
    cin>>n>>x;
    for(int i=1;i<=n;i++) cin>>a[i];
    int ans=0;
    int l=a[1]-x,r=a[1]+x;
    for(int i=2;i<=n;i++){
        int l1=a[i]-x,r1=a[i]+x;
        if(r1<l||l1>r){
            ans++;
            l=l1,r=r1;
        }
        if(l1>=l) l=l1;
        if(r1<=r) r=r1;
    }
    cout<<ans<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

2.Problem - 1702D - Codeforces

首先总的和是一定的 ，要使得删掉某些字符之后和小于等于p，求长度最大的字符串 ，那么肯定优先删除值大的字符

标记删哪些字符，以及删几个，当和小于等于p时，该标记的就都标记完了

注意一开始判断总和如果小于等于p，也就是说一个字符都不用删，那么直接输出原先的字符串（这个小细节没注意到）

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=30;
int cnt[N];
int delete1[N];
string s;
int p;
void solve() {
    cin>>s>>p;
    for(int i=1;i<=26;i++) cnt[i]=0,delete1[i]=0;
    int len=s.size();
    for(int i=0;i<len;i++){
        cnt[s[i]-'a'+1]++;
    }
    int sum=0;
    for(int i=1;i<=26;i++) sum+=i*cnt[i];
    if(sum<=p){
        cout<<s<<endl;
        return;
    }
//    cout<<sum<<endl;
    for(int i=26;i>=1;i--){
        for(int j=0;j<cnt[i];j++){
            sum-=i;
            delete1[i]++;
            if(sum<=p) break;
        }
        if(sum<=p) break;
    }
    string tmp="";
    for(int i=0;i<len;i++){
        if(delete1[s[i]-'a'+1]==0) tmp+=s[i];
        else delete1[s[i]-'a'+1]--;
    }
    cout<<tmp<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

3.Problem - 1883C - Codeforces

k无非就只能等于2或3或4或5

那么就分情况讨论，要注意判断的优先级

如下是一开始犯的优先级错误:

for(int i=1;i<=n;i++){
    if(a[i]%4==0){
        cout<<0<<endl;
        return;
    }
    else if((a[i]+1)%4==0){
        cout<<1<<endl;
        return;
    }
}

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=1e5+10;
int a[N];
int n,k;
void solve() {
    cin>>n>>k;
    for(int i=1;i<=n;i++) cin>>a[i];
    int cnt=0;//偶数的个数
    for(int i=1;i<=n;i++){
        if(a[i]%2==0) cnt++;
    }
    if(k==2){
        for(int i=1;i<=n;i++){
            if(a[i]%2==0){
                cout<<0<<endl;
                return;
            }
        }
        cout<<1<<endl;
        return;
    }
    if(k==4){
        if(cnt>=2){//偶数个数大于等于2
            cout<<0<<endl;
            return;
        }
        for(int i=1;i<=n;i++){
            if(a[i]%4==0){
                cout<<0<<endl;
                return;
            }
        }
        for(int i=1;i<=n;i++){
            if((a[i]+1)%4==0){
                cout<<1<<endl;
                return;
            }
        }
        if(cnt==1) cout<<1<<endl;
        else cout<<2<<endl;
        return;
    }
    if(k==3){
        int ans=2e9;
        for(int i=1;i<=n;i++){
            if(a[i]%3==0){
                cout<<0<<endl;
                return;
            }
            int d=a[i]/3+1;
            ans=min(ans,d*3-a[i]);
        }
        cout<<ans<<endl;
        return;
    }
    if(k==5){
        int ans=2e9;
        for(int i=1;i<=n;i++){
            if(a[i]%5==0){
                cout<<0<<endl;
                return;
            }
            int d=a[i]/5+1;
            ans=min(ans,d*5-a[i]);
        }
        cout<<ans<<endl;
        return;
    }
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

4.Problem - 1876A - Codeforces

贪心，用最小代价去传递消息

首先传给第一个人的代价一定是p

我们按代价从小到大排个序，然后如果代价小于p，那么就以小代价传消息，否则就以代价p传消息

这里用到队列，类似于bfs（哈哈，我都不知道自己咋想到的队列，感觉方法真妙）

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=1e5+10;
struct node{
    int a,b;
    bool operator<(const node &W)const{
        return b<W.b;
    }
}s[N];
int n,p;
void solve() {
    cin>>n>>p;
    for(int i=1;i<=n;i++) cin>>s[i].a;
    for(int i=1;i<=n;i++) cin>>s[i].b;
    if(n==1){
        cout<<p<<endl;
        return;
    }
    sort(s+1,s+1+n);
    int ans=0;
    ans+=p;
    queue<node>q;
    q.push({s[1].a,s[1].b});
    int idx=1;
    while(q.size()){
        auto t=q.front();
        q.pop();
        if(t.b<p){
            for(int i=1;i<=t.a;i++){
                idx++;
                q.push({s[idx].a,s[idx].b});
                ans+=t.b;
                if(idx==n){
                    cout<<ans<<endl;
                    return;
                }
            }
        }
        else{
            ans+=p*(n-idx);
            break;
        }
    }
    cout<<ans<<endl;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

5.Problem - 1695B - Codeforces

极限过题，马上要去上课了，原本想着这一发不过就先不做了，没想到直接过了

博弈论

如果n是偶数的话，那么Mike操作1，Joe操作2，...Mike操作2*k-1,Joe操作2*k，然后操作的位置都是固定，那么最优肯定是让自己石头减的越慢越好，每次都只拿一个石头，那么只要看最少的石头且下标最小的是哪一个下标即可 ，如果下标是偶数，那么Mike赢，如果下标是奇数，那么 Joe赢

如果n是奇数的话，那么 肯定是Mike赢，MIke先行，Mike操作1，Joe操作2，...Mike操作2*k，最后Joe操作1，那么 Mike直接把第一堆石头全部拿走，然后 Joe要拿第一堆石头的时候，Joe就输了

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=55;
int a[N];
int n;
void solve() {
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    if(n%2==1) cout<<"Mike"<<endl;
    else {
        int x=1;
        for(int i=1;i<=n;i++){
            if(a[x]>a[i]) x=i;
        }
        if(x%2==0) cout<<"Mike"<<endl;
        else cout<<"Joe"<<endl;
    }
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}

总结：

1.第一题经典例子，之前没怎么见过

2.判断优先级，先后顺序要明确

第七组：

1.Problem - 1691B - Codeforces

会发现，如果严格递增的话，那么每个都只能选后一个，然后最后一个就没得选了

所以每个数必须至少有两个，然后同一个数所在的下标重新打乱顺序排列就行了

AC代码:

#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
const int N=1e5+10;
int a[N];
int n;
void solve() {
    cin>>n;
    vector<vector<int>>e(n);
    for(int i=1;i<=n;i++) cin>>a[i];
    int cnt=0;
    e[cnt].push_back(1);
    int sum=1;
    for(int i=2;i<=n;i++){
        if(a[i]==a[i-1]) e[cnt].push_back(i),sum++;
        else{
            cnt++;
            e[cnt].push_back(i);
            sum=1;
        }
    }
    for(int i=0;i<=cnt;i++){
        int x=e[i].size();
        if(x==1){
            cout<<-1<<endl;
            return;
        }
    }
    for(int i=0;i<=cnt;i++){
        int x=e[i].size();
        for(int j=1;j<x;j++){
            cout<<e[i][j]<<' ';
        }
        cout<<e[i][0]<<' ';
    }
    cout<<endl;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--) {
        solve();
    }
    return 0;
}