逆波兰式背景介绍
逆波兰式是一种特殊的数学表达式表示法,它的诞生背景可以追溯到20世纪30年代。当时,波兰数学家Jan Wójtowicz和Wacław Sierpiński提出了一种新的数学表达式表示法,这种表示法将运算符放在操作数之后,而不是传统的数学表达式中的运算符放在操作数之前的表示法。 这种新的表示法被称为逆波兰式,因为它与传统的波兰式数学表达式相反。传统的波兰式数学表达式是一种将运算符放在操作数之前的表示法,例如(2+3)*4。而逆波兰式则是将运算符放在操作数之后,例如2 3 + 4 *。
逆波兰式的出现主要是为了解决传统的数学表达式中的一些问题,例如括号匹配问题。在传统的数学表达式中,括号的嵌套顺序非常重要,如果括号的嵌套顺序不正确,就会导致计算结果错误。而逆波兰式则避免了括号的嵌套问题,因为它不需要使用括号来表示运算顺序。 逆波兰式的出现对计算机科学产生了重要的影响,它被广泛应用于计算机程序设计中,特别是在函数式编程和函数式编译器中。逆波兰式也被用于一些高级编程语言中,例如Lisp和Scheme。
前缀式、后缀式、中缀式的概念
二叉树表达
一个表达式可以使用一棵二叉树来进行一个存储表达,而对应的前、中、后序遍历的结果对应的就是前缀式、中缀式、后缀式。
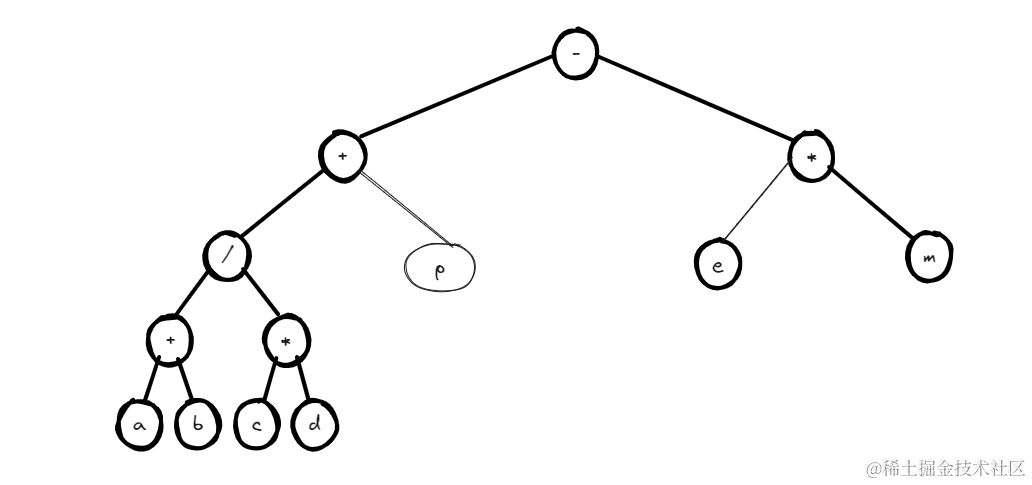
例如表达式**((a+b)/(cd)+p)-(cm)**
对应二叉树:
中缀式
中缀式就是我们人能够认识的表达式格式,如((a+b)/(cd)+p)-(cm),而对应的就是该二叉树的中序遍历得到的结果
前缀式
前缀式就是将该二叉树进行前序遍历得到的结果:-+/+abcdpem
后缀式
后缀式就是将该二叉树进行后序遍历得到的结果:ab+cd*/p+em*-
总结
从前中后序的结构其实不难得出一个很明显的结论:
前缀式往往会将运算符号放在前面,数字放在后面,而后缀式往往是将数字放在前面,运算符号放在后面。
波兰式常见面试算法题:
1.根据前缀式、后缀式求出表达式结果:
后缀式求值(leetcode地址:https://leetcode.cn/problems/8Zf90G/ )
题目简单描述:
根据[ 逆波兰表示法]求该后缀表达式的计算结果。
有效的算符包括 `+`、`-`、`*`、`/` 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入: tokens = ["2","1","+","3","*"]
输出: 9
解释: 该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
其实这个题型是特别简单的,大概思路就是直接遍历tokens,遇见数字就将其放入栈中,遇见运算符将数字取出两个进行运算再将结果放入栈中…即便没遇见过也是很容易想出来的
Go代码展示:
func evalRPN(tokens []string) int {
stack := []int{}
for _, token := range tokens {
val, err := strconv.Atoi(token)
if err == nil {
stack = append(stack, val)
} else {
num1, num2 := stack[len(stack)-2], stack[len(stack)-1]
stack = stack[:len(stack)-2]
switch token {
case "+":
stack = append(stack, num1+num2)
case "-":
stack = append(stack, num1-num2)
case "*":
stack = append(stack, num1*num2)
default:
stack = append(stack, num1/num2)
}
}
}
return stack[0]
}
前缀式求值与其原理相同,建议自己可以尝试一下,不过leetcode没有类似题目
中缀式转前缀式、中缀式转后缀式
这种题型其实也挺常考的,之前面试字节一面就出了一个中缀式转后缀式的算法题。。
这类题就没这么容易了,因为有括号的原因,所以其实需要考虑的情况是比较多的。不过基本原理依旧是使用栈~
此题我依旧只解析中缀转后缀的例子,因为中缀转前缀原理依旧一致。
例如该中缀式((a+b)/(cd)+p)-(cm)
其基本原理依旧是遍历一遍中缀式,对’(‘、’)'、‘运算符’、'数字’都会有不同的处理方式
case 1’数字’:直接将其放入结果数组
case 2 ‘(’: 放入栈中
case 3 ‘)’:将其与对应左括号之间的符号出栈放入结果数组
case 4 ‘运算符’:若在栈底, 在括号底, 或者操作符优先级比栈顶的高, 则操作符入栈;否则出栈
举个例子:((a+b)/(cd)+p)-(cm) ---->ab+cd*/p+cm*-
'(' --> stack=['('] res=[]
'(' --> stack['(' , '('] res=[]
'a' --> stack['(' , '('] res=['a']
'+' --> stack['(' , '(' , '+'] res=['a']
'b' --> stack['(' , '(' , '+'] res=['a','b']
')' --> stack['('] res=['a','b','+']
'/' --> stack['(','/'] res=['a','b','+']
'(' --> stack['(','/','('] res=['a','b','+']
'c' --> stack['(','/','('] res=['a','b','+' , 'c']
'*' --> stack['(','/','(' , '*'] res=['a','b','+' , 'c']
'd' --> stack['(','/','(' , '*'] res=['a','b','+' , 'c' , 'd']
')' --> stack['(','/'] res=['a','b','+' , 'c' , 'd','*']
'+' --> stack['(','+'] res=['a','b','+' , 'c' , 'd','*','/']
'p' --> stack['(','+'] res=['a','b','+' , 'c' , 'd','*','/','p']
')' --> stack[] res=['a','b','+' , 'c' , 'd','*','/','p','+']
'-' --> stack['-'] res=['a','b','+' , 'c' , 'd','*','/','p','+']
'(' --> stack['-','('] res=['a','b','+' , 'c' , 'd','*','/','p','+']
'c' --> stack['-','('] res=['a','b','+' , 'c' , 'd','*','/','p','+','c']
'*' --> stack['-','(','*'] res=['a','b','+' , 'c' , 'd','*','/','p','+','c']
'm' --> stack['-','(','*'] res=['a','b','+' , 'c' , 'd','*','/','p','+','c',''m']
')' --> stack[] res=['a','b','+' , 'c' , 'd','*','/','p','+','c',''m','*','-']
每一步按照上述原理进行,就很容易理解如何将中缀式转为后缀式了。而转前缀式同理,感兴趣的小伙伴可以自行去推导一下步骤~