算法--数据结构

news2024/12/28 3:25:25

这里写目录标题

本节内容
链表与邻接表
- 链表
- - 主要思想
  - 链表操作
  - - 初始化+在head结点后面插入
    - 普通插入
    - 删除操作
  - 例子
- 双链表（双向循环链表）
- - 主要思想
  - 操作
  - - 初始化+双向插入
    - 删除第k个点
- 邻接表
- - 主要思想
栈和队列
- 栈
- - 主要思想
  - 主要操作
- 队列
- - 主要思想
  - 操作
单调栈与单调队列
- 单调栈
- - 主要思想
  - 例题
一级目录
- 二级目录
- 二级目录
- 二级目录
一级目录
- 二级目录
- 二级目录
- 二级目录
一级目录
- 二级目录
- 二级目录
- 二级目录

本节内容

在这里插入图片描述

链表与邻接表

链表

主要思想

在这里插入图片描述
因为用真正的链表来写算法的话会new很多东西而new的过程是非常慢的

所以我们要用数组来写链表
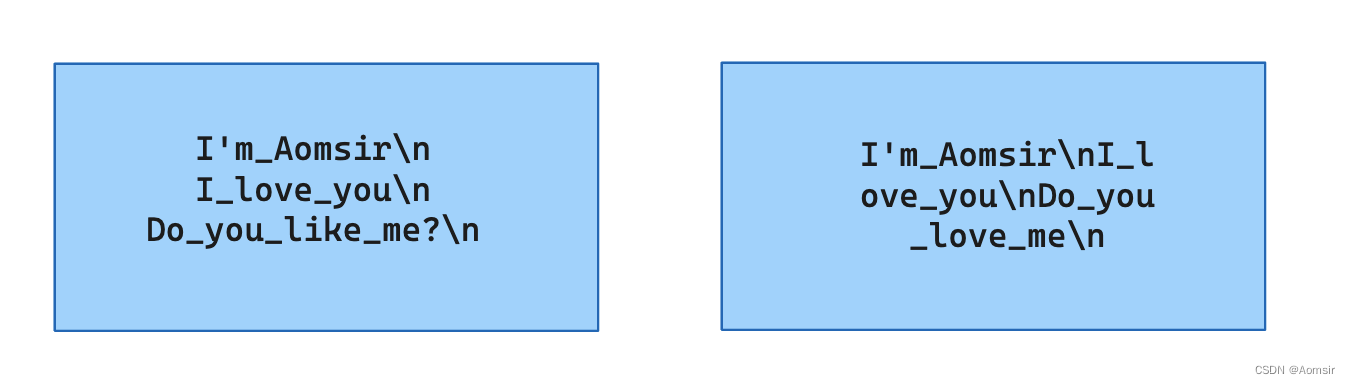
如上图链表分为单链表和双链表单链表主要是邻接表主要作用是存储图和树

e[]数组用来存储各个结点的val值而ne[]数组用来存储各个结点的next指针而表示在数组里就是存储下一个结点的数组下标
最后的空地址用-1表示
head表示指向头结点的指针实际上就是头结点的下标

！！所有的结点都在e[]数组里但是他们的排序不是按照e[]的下标按照顺序连续排序的他们的排序是一个链表存在ne[]数组里
e[k] 是指下标为k的e[]数组中的值也就是在e[]数组中下标为k的值
ne[k] 是指在e[]数组中下标为k的结点下一个结点在e[]数组中的位置（下标）
在这里插入图片描述
同时会定义一个int变量idx 存储当前操作的点的下标实质上发挥着指针的作用
他会指针一个e[]数组中最新的可用的位置用来新建一个结点

链表操作

初始化+在head结点后面插入

在这里插入图片描述
初始化就是将head改为-1 意思是head指向-1位置的空间也就是空指针
然后idx可以更新为0 因为e[]数组中第一个可用位置就是下标为0的位置

插入
首先新建结点 e[idx]=x

之后next域指向头结点 ne[idx]=head
因为head存储的就是第一个数据的下标

之后将head指向新插入的结点 head=idx

最后idx后移更新最新的可操作的位置的下标

普通插入

在这里插入图片描述
将x插入到下标是k的结点的后面

删除操作

在这里插入图片描述

在这里插入图片描述
注意中括号里就是存储的下标

！！所有的结点都在e[]数组里但是他们的排序不是按照e[]的下标按照顺序连续排序的他们的排序是一个链表存在ne[]数组里
注意 k结点的下一个结点的下标不一定是k+1 而是ne[k] 这就是k结点的下一个结点在e[]数组中的下标

而e[]数组中的元素的位置排序是按照生成的时间来排序的因为生成一个结点就是在e[]数组中新建一个数据
比如第k个插入的点他的下标是k-1 这里说的就是在e[]数组中的下标

例子

在这里插入图片描述

在这里插入图片描述
注意光标所在行给了特判

双链表（双向循环链表）

主要思想

在这里插入图片描述
在单链表的基础上加了两个指针域函数一个是l[ ] 一个是r[ ]

因为是双向循环链表可以让0号位置的空间是头结点
1号位置是尾结点
这样的话 head的值就是0 tail（指向尾结点的指针）的值就是1

操作

初始化+双向插入

在这里插入图片描述
初始化因为是循环链表头结点和尾结点也是双向链接所以 r[0]=1 l[1]=0;
同时因为0 1 的位置被占用了所以idx初始化是2

插入：
在下标为k的节点后面插入在这里插入图片描述
先新建结点 e[idx]=x
首先更新新节点的r 和 l
然后更新两端结点的指针数组
先更新右端点的 l[ ]数组再更新左端点的 r[ ] 数组

不然如果先更新r 那么就找不到右端点的下标了也就是找不到右端点了

在下标为k的点的左边插入
在这里插入图片描述
在k左边插入实际上就是k的前一个结点的右边插入所以改一下函数输入就行 add（l[k],x）

删除第k个点

在这里插入图片描述
将左边点的r 更新为右边点的下标
将右边点的l 更新为左边点的下标

邻接表

主要思想

在这里插入图片描述
就是将所有节点的邻节点用链表存了起来

栈和队列

栈

主要思想

先进后出

主要操作

在这里插入图片描述
tt是栈顶指针也就是栈顶下标初始值为0（主要目的是好判断是不是空因为初始化为0之后一旦有元素插入那么tt>0）

队列

主要思想

先进先出

操作

在这里插入图片描述
hh表示队头下标 tt表示队尾下标
tt初始化为-1）（这里不用再向栈一样用tt>0来判断是不是为空了直接用hh<=tt 来判断是不是有元素所以tt就可以初始化为-1 这样插入元素的时候直接从下标0开始）
hh初始化为0
(不进行初始化默认是0)

单调栈与单调队列

在这里插入图片描述

单调栈

主要思想

在这里插入图片描述
单调栈的题型：
在i的位置插入一个数x
找到在该序列中左边离x最近的且小于x的数

单调栈主要就是将一个序列找到他的性质将其单调化如下：
在这里插入图片描述
我们可以把i左边的数全部加入栈中
然后对该栈进行一些处理把那些相对位置在左边的且较大的数弹出这样整个栈就变成了一个单调递增的栈与新插入进来的数进行比较的时候就比较方便（进行该步时先暂时不考虑是否相等的问题因为现在先处理的是研究点x放入之前的状态）