分类目录:《深入理解强化学习》总目录
到目前为止,我们已经探讨了评估动作价值的方法,并使用这些估计值来选择动作。这通常是一个好方法,但并不是唯一可使用的方法。我们针对每个动作
a
a
a考虑学习一个数值化的偏好函数
H
t
(
a
)
H_t(a)
Ht(a)。偏好函数越大,动作就越频繁地被选择,但偏好函数的概念并不是从“收益"的意义上提出的。只有一个动作对另一个动作的相对偏好才是重要的,如果我们给每一个动作的偏好函数都加上1000,那么对于按照如下Softmax分布(吉布斯或玻尔兹曼分布)确定的动作概率没有任何影响:
Pr
{
A
t
=
a
}
=
e
H
t
(
a
)
∑
i
=
1
k
e
H
t
(
i
)
=
π
t
(
a
)
\text{Pr}\{A_t=a\}=\frac{e^{H_t(a)}}{\sum_{i=1}^ke^{H_t(i)}}=\pi_t(a)
Pr{At=a}=∑i=1keHt(i)eHt(a)=πt(a)
其中, π t ( a ) \pi_t(a) πt(a)是一个新的且重要的定义,用来表示动作 a a a在时刻时被选择的概率。所有偏好函数的初始值都是一样的(如: ∀ A : H 1 ( a ) = 0 \forall A:H_1(a)=0 ∀A:H1(a)=0),所以每个动作被选择的概率是相同的。
基于随机梯度上升的思想,本文提出了一种自然学习算法。在每个步骤中,在选择动作
A
t
A_t
At并获得收益
R
t
R_t
Rt之后,偏好函数将会按如下方式更新:
H
t
+
1
(
A
t
)
=
H
t
(
A
t
)
+
α
(
R
t
−
R
t
ˉ
)
(
1
−
π
t
(
A
t
)
)
H
t
+
1
(
a
)
=
H
t
(
a
)
−
α
(
R
t
−
R
t
ˉ
)
π
t
(
a
)
,
∀
a
≠
A
t
\begin{aligned} H_{t+1}(A_t)&=H_t(A_t)+\alpha(R_t-\bar{R_t})(1-\pi_t(A_t)) \\ H_{t+1}(a)&=H_t(a)-\alpha(R_t-\bar{R_t})\pi_t(a) \end{aligned}\quad ,\forall a\neq A_t
Ht+1(At)Ht+1(a)=Ht(At)+α(Rt−Rtˉ)(1−πt(At))=Ht(a)−α(Rt−Rtˉ)πt(a),∀a=At
其中, α \alpha α是一个大于0的数,表示步长。 R t ∈ R R_t\in R Rt∈R是在时刻 t t t内所有收益的平均值,可以按文章《深入理解强化学习——多臂赌博机:增量式实现》所述逐步计算,若是非平稳问题,则可以参考文章《深入理解强化学习——多臂赌博机:非平稳问题》。 R t ˉ \bar{R_t} Rtˉ作为比较收益的一个基准项。如果收益高于它,那么在未来选择动作的概率就会增加,反之概率就会降低,未选择的动作被选择的概率上升。
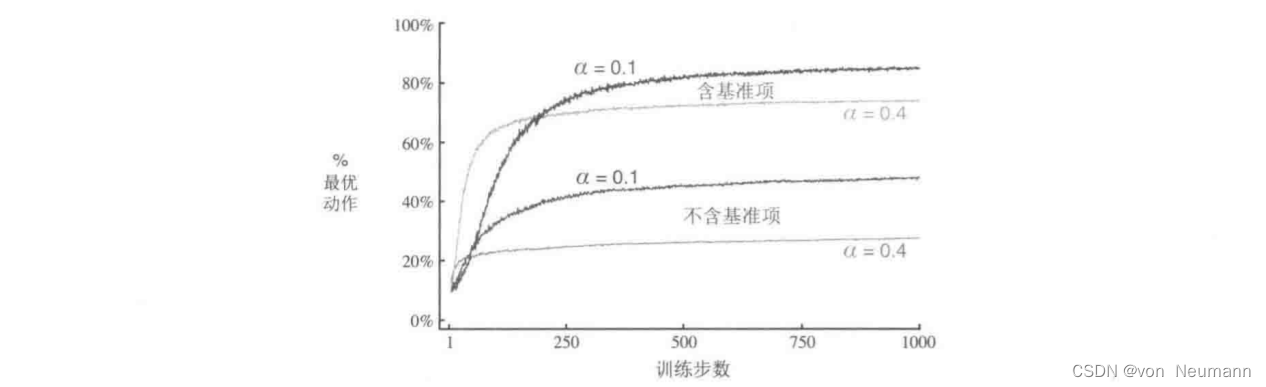
下图展示了在一个10臂测试平台问题的变体上采用梯度赌博机算法的结果,在这个问题中,它们真实的期望收益是按照平均值为
+
4
+4
+4而不是
0
0
0(方差与之前相同)的正态分布来选择的。所有收益的这种变化对梯度赌博机算法没有任何影响,因为收益基谁项计它可以马上适应新的收益水平。如果没有基准项(即把
R
t
ˉ
\bar{R_t}
Rtˉ设为常数0),那么性能将显著降低,如图所示:
参考文献:
[1] 张伟楠, 沈键, 俞勇. 动手学强化学习[M]. 人民邮电出版社, 2022.
[2] Richard S. Sutton, Andrew G. Barto. 强化学习(第2版)[M]. 电子工业出版社, 2019
[3] Maxim Lapan. 深度强化学习实践(原书第2版)[M]. 北京华章图文信息有限公司, 2021
[4] 王琦, 杨毅远, 江季. Easy RL:强化学习教程 [M]. 人民邮电出版社, 2022