挑战100天 AI In LeetCode Day08(热题+面试经典150题)
- 一、LeetCode介绍
- 二、LeetCode 热题 HOT 100-10
- 2.1 题目
- 2.2 题解
- 三、面试经典 150 题-10
- 3.1 题目
- 3.2 题解
一、LeetCode介绍

LeetCode是一个在线编程网站,提供各种算法和数据结构的题目,面向程序员、计算机科学专业学生和技术爱好者等人群,旨在帮助他们提高算法和编程技能。LeetCode上的问题通常来自各种技术公司的面试题目,因此它也是程序员面试准备的重要资源之一。
LeetCode上的问题涵盖了各种难度级别,从入门级到专家级都有不同难度的题目可供练习。用户可以选择使用不同的编程语言提交答案,LeetCode能够对结果进行评估并返回测试结果。
除了题目外,LeetCode还提供了讨论区、排行榜等社区功能,用户可以在这里交流学习心得、解决疑难问题,并与其他用户比较自己的做题成绩。
挑战100天 AI In LeetCode是基于LeetCode题库,借助AI的能力进行解题、并学习其解题过程。
二、LeetCode 热题 HOT 100-10
2.1 题目
回文数
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
例如,121 是回文,而 123 不是。
示例 1:
输入:x = 121
输出:true
示例 2:
输入:x = -121
输出:false
解释:从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:
输入:x = 10
输出:false
解释:从右向左读, 为 01 。因此它不是一个回文数。
提示:
-231 <= x <= 231 - 1
进阶:你能不将整数转为字符串来解决这个问题吗?
2.2 题解
解题思路:
- 首先判断整数x是否为负数,如果是负数,则直接返回false,因为负数不可能是回文数。
- 然后判断整数x是否小于0,如果是小于0,则将其转为正数,因为负数的倒序就是它的正序。
- 接下来,将整数x转换为字符串,方便进行回文判断。
- 从字符串的两端开始比较字符,如果发现不相等的字符,则返回false。
- 如果所有字符都相等,则返回true。
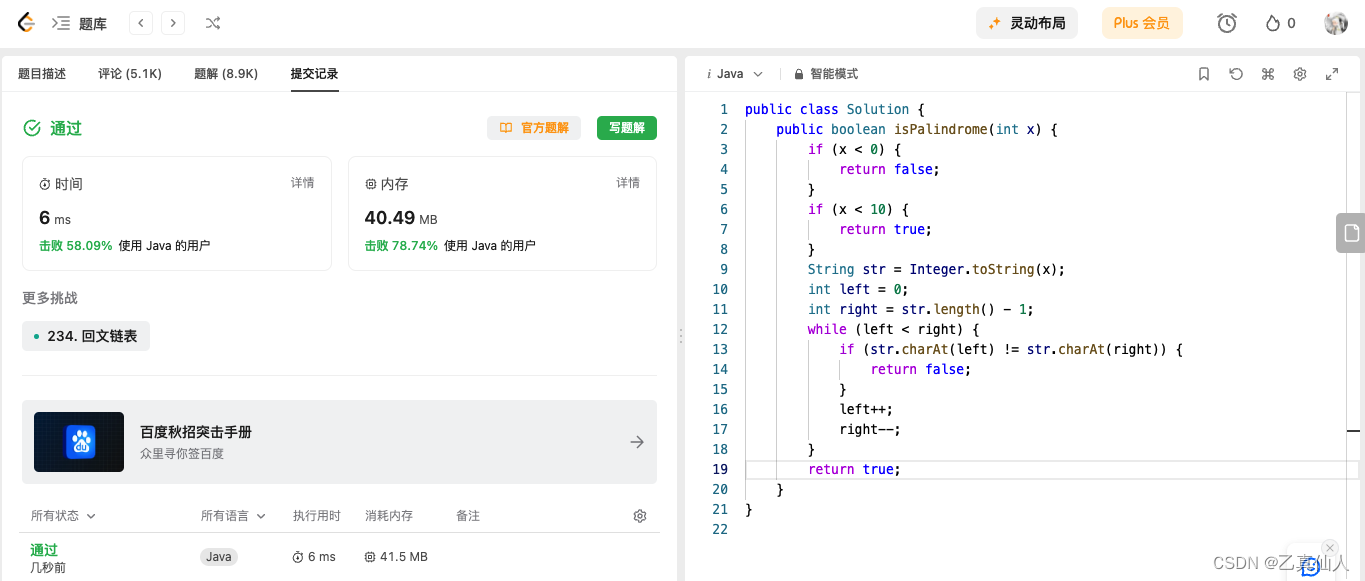
public boolean isPalindrome(int x) {
if (x < 0) {
return false;
}
if (x < 10) {
return true;
}
String str = Integer.toString(x);
int left = 0;
int right = str.length() - 1;
while (left < right) {
if (str.charAt(left) != str.charAt(right)) {
return false;
}
left++;
right--;
}
return true;
}
三、面试经典 150 题-10
数组 / 字符串
3.1 题目
跳跃游戏 II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
提示:
1 <= nums.length <= 10 4
0 <= nums[i] <= 1000
题目保证可以到达 nums[n-1]
3.2 题解
解题思路:
- 初始化一个变量 maxPos,表示当前能够到达的最远位置。
- 初始化一个变量 end,表示当前跳跃的边界。
- 初始化一个变量 step,表示跳跃的次数。
- 遍历数组,对于每个元素 nums[i],更新 maxPos 为 max(maxPos, i + nums[i])。
- 如果 i == end,说明已经到达当前跳跃的边界,需要更新 end 为 maxPos,并将 step 加 1。
- 遍历结束后,返回 step。
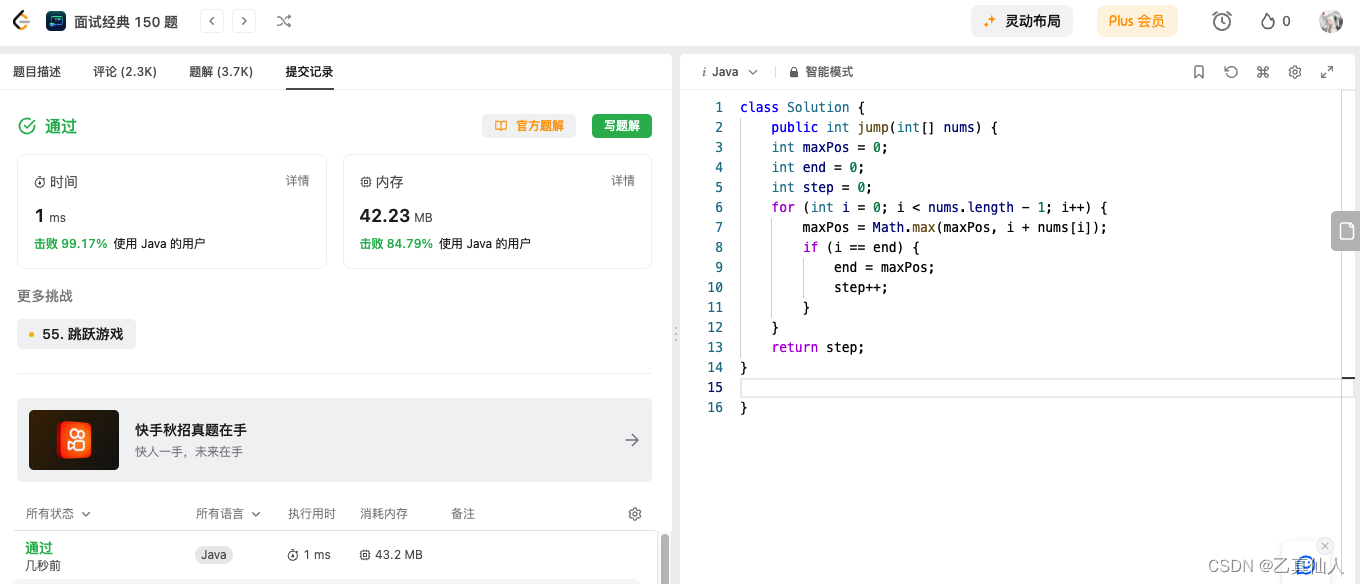
public int jump(int[] nums) {
int maxPos = 0;
int end = 0;
int step = 0;
for (int i = 0; i < nums.length - 1; i++) {
maxPos = Math.max(maxPos, i + nums[i]);
if (i == end) {
end = maxPos;
step++;
}
}
return step;
}
至此,挑战100天 AI In LeetCode Day08(热题+面试经典150题)完成,后续会持续调整;查阅过程中若遇到问题欢迎留言或私信交流。