一、二分
1.二分性质
二分的本质:二分可以将边界点二分出来(即一部分满足这个条件,一部分不满足这个条件)
二分的时候也一定有解
2.整数二分
1.寻找红色边界点x
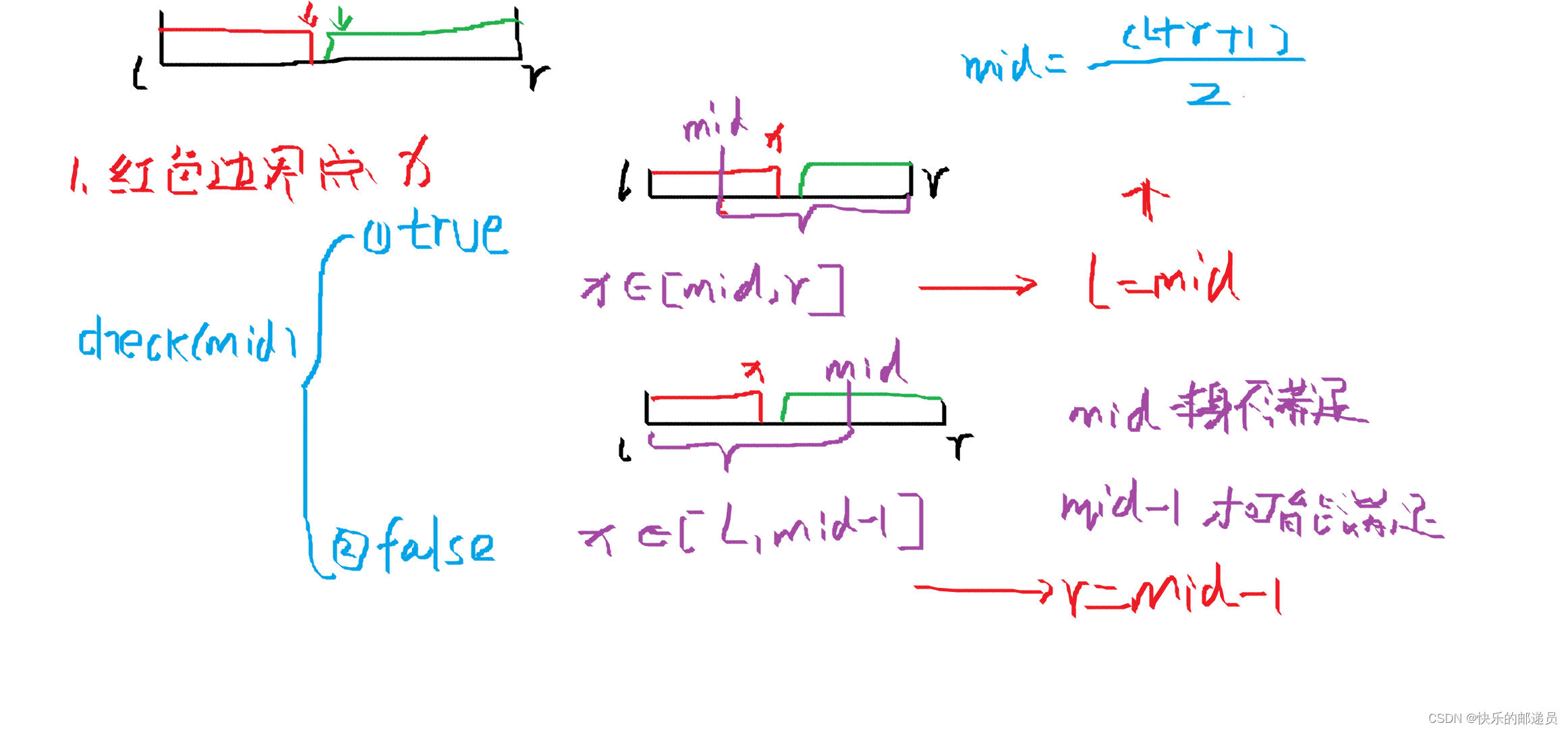
int l=0,r=n-1;
while(l<r)
{
int mid=(l+r+1)/2;
if(check(mid))
l=mid;//当l=mid时,mid=(l+r+1)/2
else
r=mid-1;
}
return l;(1) 寻找红色边界点推导思路
int mid=(l+r+1)/2;//当出现l=mid就需要补充加1
if(check(mid))
1.true [mid,r] l=mid;
2.false [l,mid-1] r=mid-1;
(2)为什么mid=(l+r+1)/2?
当l=r-1时,mid=(l+r)/1=(l+l+1)/2=l;
if(check(mid)==true)//会死循环
l=mid;
所以l=l,l没有变,可能会死循环
2.寻找绿色边界点y
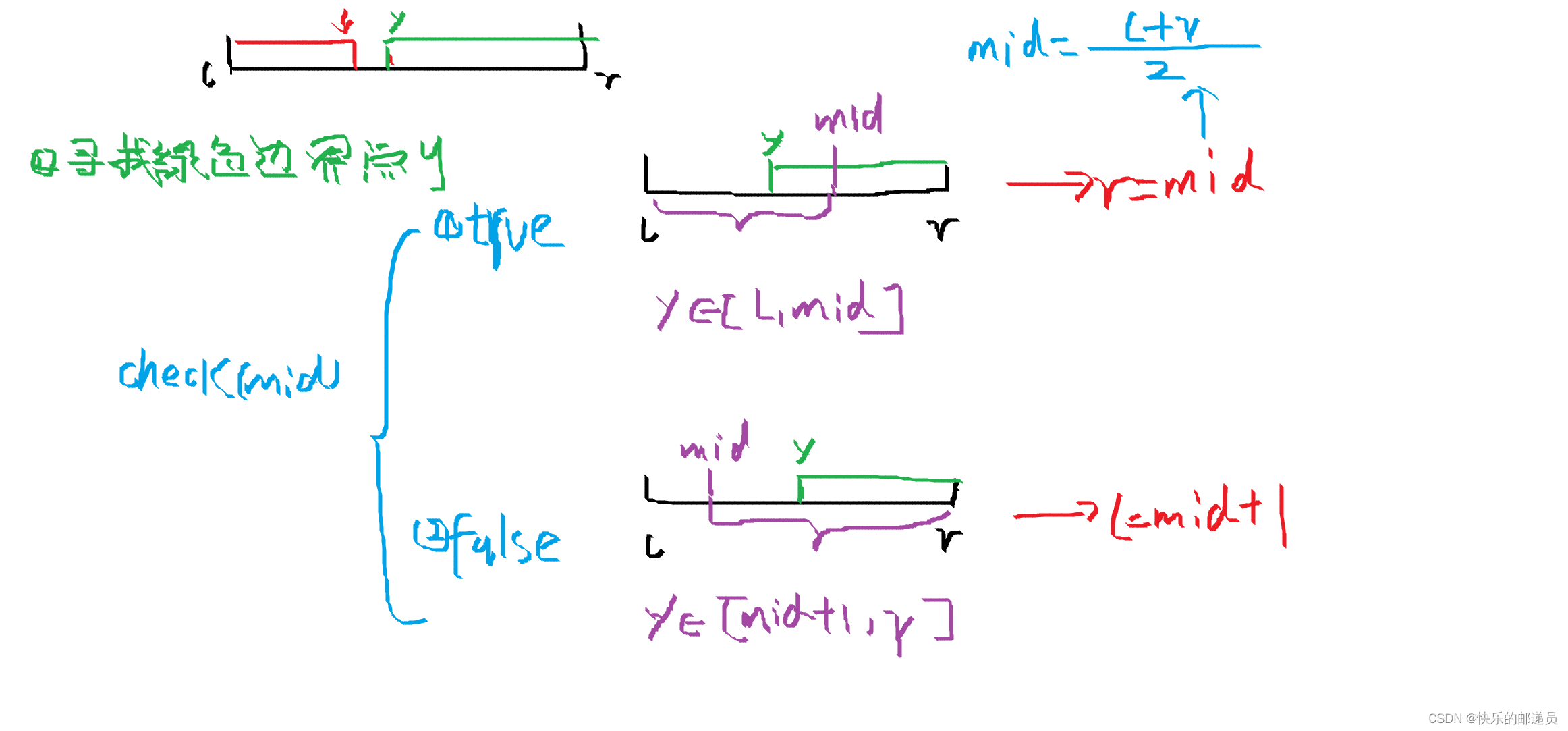
(1)找绿色边界点推导思路
int mid=(l+r)/2;
if(check(mid))
1.true [l,mid] r=mid;
2.false [mid+1,r] l=mid+1;
3.浮点二分
1.答案范围不能取到[0,x],可以取[0,max(1,x)];
比如x=0.01
l=0 r=x=0.01
sqrt(0.01)=0.1,答案没有在[0,0.1]之间
2.当需要保留6位小数的时候,6+2=8, 1e-8
1.先确定边界范围 int l=x,int r=y;
2.进行二分
while(r-l>1e-8)
二分
二、相关例题
acwing789. 数的范围
一、题目要求
给定一个按照升序排列的长度为 n 的整数数组,以及 q个查询。
对于每个查询,返回一个元素 k 的起始位置和终止位置(位置从 0 开始计数)。
如果数组中不存在该元素,则返回 -1 。
输入格式
第一行包含整数 n 和 q,表示数组长度和询问个数。
第二行包含 n个整数(均在 1∼10000范围内),表示完整数组。
接下来 q行,每行包含一个整数 k,表示一个询问元素。
输出格式
共 q行,每行包含两个整数,表示所求元素的起始位置和终止位置。
如果数组中不存在该元素,则返回 -1。
数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000
输入样例:
6 3
1 2 2 3 3 4
3
4
5
输出样例:
3 4
5 5
-1 -1
二、思路
1.数组是按升序排列的
2.先求出最左边的第一个数,return l,如果a[l]!=x的话,则说明该数组中不存在这个数
即:

2.在求出最右边第一个数
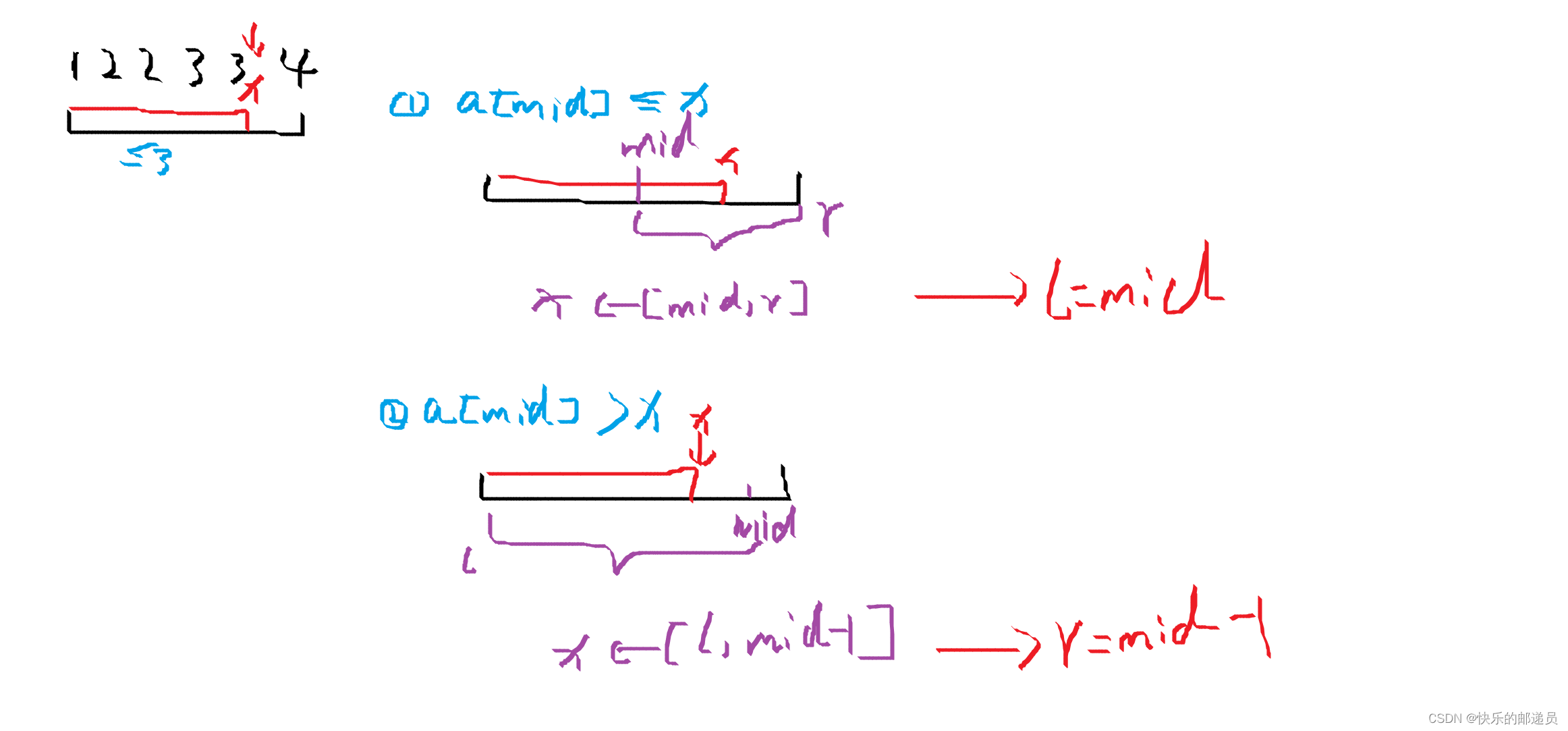
三、代码
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
using namespace std;
const int N=1e5+10;
const int inf=0x3f3f3f3f;
int n,m;
int a[N];
int leftfind(int x)//相当于寻找绿色边界点
{
int l=0,r=n-1;
while(l<r)
{
int mid=(l+r)/2;
if(a[mid]>=x)
{
r=mid;
}
else
{
l=mid+1;
}
}
return l;
}
int rightfind(int x)//相当于寻找红色边界点
{
int l=0,r=n-1;
while(l<r)
{
int mid=(l+r+1)/2;
if(a[mid]<=x)
l=mid;
else
r=mid-1;
}
return l;
}
void solve()
{
cin>>n>>m;
int i;
for(i=0;i<n;i++)
{
cin>>a[i];
}
while(m--)
{
int x;
cin>>x;
int l=leftfind(x);
if(a[l]!=x)
cout<<"-1 -1"<<endl;
else
{
int r=rightfind(x);
cout<<l<<' '<<r<<endl;
}
}
}
signed main()
{
int t=1;
while(t--)
{
solve();
}
return 0;
}
acwing790. 数的三次方根
一、题目要求
给定一个浮点数 n,求它的三次方根。
输入格式
共一行,包含一个浮点数 n。
输出格式
共一行,包含一个浮点数,表示问题的解。
注意,结果保留 6 位小数。
数据范围
−10000≤n≤10000
输入样例:
1000.00
输出样例:
10.000000二、思路
1.先确定l,r的范围
2.保留6位小数,可以6+2=8 ,1e-8(精度问题)
3.二分
三、代码
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
using namespace std;
const int N=2e5+10;
const int inf=0x3f3f3f3f;
double n;
void solve()
{
cin>>n;
double l=-10000,r=10000;
while(r-l>1e-8)//结果保留6位小数,6+2=8, 1e-8;
{
double mid=(l+r)/2;
if(mid*mid*mid>=n)
r=mid;
else
l=mid;
}
printf("%lf\n",l);
}
signed main()
{
int t=1;
while(t--)
{
solve();
}
return 0;
}