目录
7-1 汉诺塔问题
7-2 逆序对
7-3 前t个组合结果
7-4 跳马问题
7-5 加油站之最小加油次数
7-6 删数问题
7-1 因子分解
7-2 英雄出场王
7-3 最佳组队问题
7-4 回文串的切割
7-5 和谐宿舍
7-6 h0221.激光炸弹
7-1 小H分糖果
7-2 子集和问题
7-3 数列游戏
7-4 叠猫猫
7-5 范围和
7-6 ACM宣传
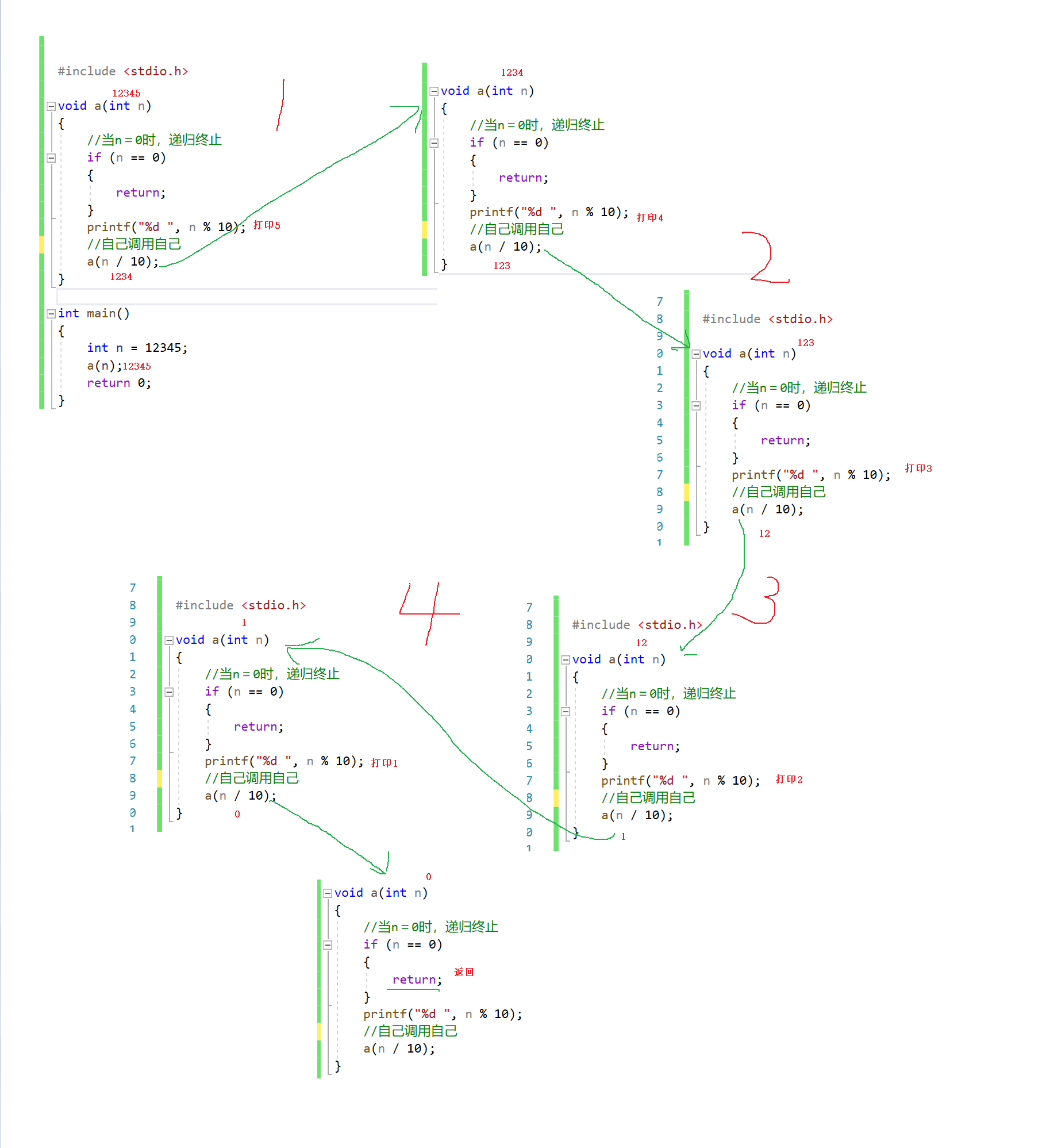
7-1 汉诺塔问题
分数 20
全屏浏览题目
切换布局
作者 李祥
单位 湖北经济学院
汉诺塔是一个源于印度古老传说的益智玩具。据说大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘,大梵天命令僧侣把圆盘移到另一根柱子上,并且规定:在小圆盘上不能放大圆盘,每次只能移动一个圆盘。当所有圆盘都移到另一根柱子上时,世界就会毁灭。

请编写程序,输入汉诺塔圆片的数量,输出移动汉诺塔的步骤。
输入格式
圆盘数
起始柱 目的柱 过度柱
输出格式
移动汉诺塔的步骤
每行显示一步操作,具体格式为:
盘片号: 起始柱 -> 目的柱
其中盘片号从 1 开始由小到大顺序编号。
输入样例
3
a c b
输出样例
1: a -> c
2: a -> b
1: c -> b
3: a -> c
1: b -> a
2: b -> c
1: a -> c
#include<stdio.h>
//AUTHOR:CHENG XIANGBO
void hanoi(int n,char ,char ,char );
int main(){
int n;//运行次数为2^n-1次,64让计算机跑100年,平时测试上限为22
scanf("%d",&n);
getchar();//吃掉回车
char a,b,c;
scanf("%c %c %c",&a,&c,&b);
hanoi(n,a,c,b);//hanoi(盘号,起始盘,目的盘,过度盘)
}
void hanoi(int n,char a,char c,char b){
if(n==1)
printf("1: %c -> %c\n",a,c);//直接把盘子A -> C
else{
hanoi(n-1,a,b,c);//hanoi(盘号-1,A -> B)
printf("%d: %c -> %c\n",n,a,c);
hanoi(n-1,b,c,a);//hanoi(盘号-1,B -> C)
}
}
7-2 逆序对
分数 20
全屏浏览题目
切换布局
作者 c++课程组
单位 湖州师范学院
求逆序对。
输入格式:
第一行是一个整数n,(n<=1000,000)表示输入序列的长度,接下来一行是n个整数(每个数的绝对值小于109)。
输出格式:
一个数,表示逆序对个数(逆序即任意一对数前面的数比后面的数大即为一对逆序对)。
输入样例:
10
1 3 5 7 9 8 4 2 6 10
输出样例:
逆序对对数可能很大,计数器要用long long:
14
说明:样例中如1和3不是逆序对,而3和2是1对逆序对,例子中共有14对逆序对。题目中可能有某些数字出现多次的情况。
#include <stdio.h>
#define N 1000000
int n,a[N],b[N];
long long cnt=0;
void f(int L,int R)
{
if(L==R) return;
int m=(L+R)/2;
int k1=L,k2=m+1,k=L;
f(L,m);
f(m+1,R);
while(k1<=m&&k2<=R)
{
if(a[k1]<=a[k2])
{
b[k]=a[k1];
k++,k1++;
}
else{
b[k]=a[k2];
k++,k2++;
cnt=cnt+m-k1+1;
}
}
while(k1<=m)
{
b[k]=a[k1];
k++,k1++;
}
while(k2<=R)
{
b[k]=a[k2];
k++,k2++;
}
for(int i=L;i<=R;i++)
a[i]=b[i];
}
int main()
{
int i ;
scanf("%d",&n);
for(i=1;i<=n;i++)
scanf("%d",&a[i]);//cin>>a[i];
f(1,n);
printf("%lld",cnt);
return 0;
}7-3 前t个组合结果
分数 20
全屏浏览题目
切换布局
作者 高见元
单位 湖北经济学院
组合结果
找出从自然数1、2、... 、n(0<n<=30)中任取r(0<r<=n)个数的组合,输出其中前t个组合结果。
输入格式:
在一行中输入n、r、t(1<=t<=C(n,r))。
输出格式:
按特定顺序输出前t个组合结果,每一个组合结果占一行,含第一个整数在内的每一个整数前面都用一个空格,最后一个整数后面没有空格。
特定顺序:每一个组合结果中的值从大到小排列,组合之间按逆字典序排列。
输入样例:
在这里给出一组输入。例如:
5 3 10
6 4 8
输出样例:
在这里给出相应的输出。例如:
5 4 3
5 4 2
5 4 1
5 3 2
5 3 1
5 2 1
4 3 2
4 3 1
4 2 1
3 2 1
6 5 4 3
6 5 4 2
6 5 4 1
6 5 3 2
6 5 3 1
6 5 2 1
6 4 3 2
6 4 3 1#include <iostream>
#include <cstdio>
using namespace std;
int X[31], used[31];
int n, r, t, count;
void output()
{
for (int i = 1; i <= r; ++i)//输出r个
{
printf(" %d", X[i]);
}
putchar('\n');
}
int pruning(int i)
{
if (used[i]) return 0;
return 1;
}
void f(int k, int i)
{
if (t == count) return ;
if (k - 1 == r)//只组合r个
{
++count;
output();
}
else
{
for (;i >= 1; --i)
{
if (pruning(i))
{
X[k] = i;
used[i] = 1;
f(k + 1, i - 1);
used[i] = 0;
}
}
}
}
int main()
{
scanf("%d %d %d", &n, &r, &t);
f(1, n);
return 0;
}
7-4 跳马问题
分数 20
全屏浏览题目
切换布局
作者 高见元
单位 湖北经济学院
给定m*n(mn<=100)的棋盘,左上角的点坐标(1,1),一匹马从(1,2)点开始沿着日字型(有8种)跳完棋盘上所有点,且每一个点都只能跳一次,马每一步从(x,y)点起跳时优先选择的方向对应坐标偏移为:{2,1},{1,2},{-1,2},{-2,1},{-2,-1},{-1,-2},{1,-2},{2,-1}。有的棋盘会有很多种跳法,现在比较感兴趣的是马的第k种跳法是什么?
输入格式:
一行三个整数m,n,k。
输出格式:
输出马的第k种跳法,如果马无法跳完棋盘所有点则输出impossible,如果所有跳法数不到k种,则输出最后一种跳法 。
输入样例:
在这里给出一组输入。例如:
4 4 1
4 5 6
输出样例:
在这里给出相应的输出。例如:
impossible
20 1 16 9 12
15 8 11 4 17
2 19 6 13 10
7 14 3 18 5
说明:矩阵中整数1~m*n依次表示马所在位置,;例如1在第1行第2列,表示马起始位置,并且下一步在整数2所对应的第3行第1列。
#include<iostream>
#include<iomanip>
#include<string>
using namespace std;
int a[101][101], obj[101][101], n, m, k, back = 0, c = 0; /*a数组是棋盘
obj数组储存马调完棋盘后的每一步 跳到第c种跳法后标记back=1返回*/
int leap[8][2] = { {2,1},{1,2},{-1,2},{-2,1},{-2,-1},{-1,-2},{1,-2},{2,-1} }; /*马跳跃方向*/
void dfs(int a[][101], int x, int y, int deep) {
deep += 1; /*马跳跃一次加一*/
a[x][y] = deep;
if (deep == n * m && back == 0) {
c += 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
obj[i][j] = a[i][j];
}
}
if (c == k) {
back = 1;
}
// return; //这就是我细节出错的地方 直接return后 跳过了归零步骤,
//马跳到的最后的位置就没有清零,如果一定要return就在上面加一句:a[x][y]=0;
}
if (back == 0) {
for (int i = 0; i < 8; i++) {
x = x + leap[i][0];
y = y + leap[i][1];
if (x >= 1 && x <= n && y >= 1 && y <= m && a[x][y] == 0) {
dfs(a, x, y, deep);
}
x = x - leap[i][0];
y = y - leap[i][1];
}
if (back == 0)
a[x][y] = 0; /*清零步骤*/
}
}
int main() {
cin >> n >> m >> k;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
a[i][j] = 0;
}
}
dfs(a, 1, 2, 0);
if (c == 0)
cout << "impossible";
else {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (j < m)
cout << obj[i][j] << " ";
else
cout << obj[i][j];
}
if (i < n)
cout << endl;
}
}
return 0;
}7-5 加油站之最小加油次数
分数 20
全屏浏览题目
切换布局
作者 王东
单位 贵州师范学院
一辆汽车要行驶L单位距离。最开始时,汽车上有P单位汽油,每向前行驶1单位距离消耗1单位汽油。如果在途中车上的汽油耗尽,汽车就无法继续前行,即无法到达终点。途中共有N个加油站,加油站提供的油量有限,汽车的油箱无限大,无论加多少油都没问题。给出每个加油站距离终点的距离L和能够提供的油量P,问卡车从起点到终点至少要加几次油?如果不能到达终点,输出-1。
输入格式:
第一行输入N;
接下来N行分别输入两个整数L和P。
最后一行表示汽车的起点到终点的位置L和油量P。
输出格式:
输出到达城镇所需的最少站点数,如果车无法到达城镇,则输出-1。
输入样例1:
4
4 4
5 2
11 5
15 10
25 10
输出样例1:
2
输入样例2:
4
4 4
5 2
11 5
15 10
25 1
输出样例2:
-1#include<bits/stdc++.h>
using namespace std;
struct ss{
int a;
int b;
}s[100000];
bool ssa(ss s1, ss s2){
return s1.a < s2.a;
}
int main()
{
priority_queue<int> q;
long long n, L, P, ans = 0;
cin >> n;
for(int i = 0; i < n; i ++){
cin >> s[i].a >> s[i].b;
}
cin >> L >> P;
for(int i = 0; i < n; i ++){
s[i].a = L - s[i].a;
}
sort(s,s+n,ssa);
for(int i = 0; i < n; i ++){
if(P >= L)
break;
else if(P >= s[i].a){
q.push(s[i].b);
}
else{
if(!q.empty()){
P += q.top();
q.pop();
ans ++;
i --;
}
else{
ans = -1;
break;
}
}
}
cout << ans << endl;
return 0;
}7-6 删数问题
分数 20
全屏浏览题目
切换布局
作者 任唯
单位 河北农业大学
有一个长度为n(n <= 240)的正整数,从中取出k(k < n)个数,使剩余的数保持原来的次序不变,求这个正整数经过删数之后最小是多少。
输入格式:
n和k
输出格式:
一个数字,表示这个正整数经过删数之后的最小值。
输入样例:
178543 4
输出样例:
13#include <iostream>
#include <string>
using namespace std;
int main(){
string a;
int k;
cin>>a>>k;
if (k >= a.size()) a.erase();
else while(k > 0){
int i;
for (i=0; (i<a.size()-1) && (a[i] <= a[i+1]); ++i);
a.erase(i, 1);
k--;
}
while(a.size() > 1 && a[0] == '0')
a.erase(0, 1);
cout<<a<<endl;
}
7-1 因子分解
分数 20
全屏浏览题目
切换布局
作者 c++课程组
单位 湖州师范学院
输入一个数,输出其素因子分解表达式。
输入格式:
输入一个整数 n (2≤n<10000000)。
输出格式:
输出该整数的因子分解表达式。
表达式中各个素数从小到大排列。
如果该整数可以分解出因子a的b次方,当b大于1时,写做 a^b ;当b等于1时,则直接写成a。
输入样例:
20
输出样例:
2^2*5#include<stdio.h>
int n,sum=0;
int a[100000000]={0};
int flag(int x){
int i;
if(x==1)
return 0;
if(x==2)
return 1;
for(i=2;i<=x;i++){
if(x%i==0)
return 0;
else
return 1;
}
}
void chai(int x,int y)
{
if(x==0||y>x)
return ;
while(x%y==0&&flag(y)==1)
{
x=x/y;
a[y]=a[y]+1;
}
if(a[y]>0)
sum=sum+1;
chai(x,y+1);
return ;
}
int main(){
int i,k=0;
scanf("%d",&n);
chai(n,2);
for(i=2;i<=n;i++){
if(a[i]>1){
if(k+1==sum)
printf("%d^%d",i,a[i]);
else{
printf("%d^%d*",i,a[i]);
k=k+1;
}
}
else if(a[i]==1){
if(k+1==sum)
printf("%d",i);
else{
printf("%d*",i);
k=k+1;
}
}
}
return 0;
}
7-2 英雄出场王
分数 20
全屏浏览题目
切换布局
作者 许立波
单位 浙大宁波理工学院
英雄联盟总决赛正在若火如荼的展开,盲僧、刀妹、酒桶、青钢影等各路英雄悉数登场,当一个英雄被选出场时系统自动登记其序号,出场次数最多的英雄成为出场王。给定英雄序号的出场集合T,例如,T={2,4,4,4,6,7}。其出场王是4号英雄,出场次数为3。对于给定的由n个序号组成的出场集T,计算出场王序号及其出场次数。如果出现多个出场王,请输出序号最小的那个。
输入格式:
输入数据的第1行是英雄出场集T中序号个数n(n<1000);第二行输入n个出场英雄序号(不超过5位数字的自然数)。
输出格式:
输出数据的第1行给出出场王序号,第2行是出场次数。
输入样例:
在这里给出一组输入。例如:
6
2 4 4 4 6 7
输出样例:
在这里给出相应的输出。例如:
4
3#include <stdio.h>
#include <stdlib.h>
int a[100100];
int main()
{
int n;
scanf("%d",&n);
int max=-1;
int maxnumber=0;
int x;
for(int i=0;i<n;i++)
{
scanf("%d",&x);
a[x]++;
if(a[x]>max)
{
max=a[x];
maxnumber=x;
}
}
printf("%d\n",maxnumber);
printf("%d",max);
}
7-3 最佳组队问题
分数 20
全屏浏览题目
切换布局
作者 范立新
单位 绍兴文理学院
双人混合ACM程序设计竞赛即将开始,因为是双人混合赛,故每支队伍必须由1男1女组成。现在需要对n名男队员和n名女队员进行配对。由于不同队员之间的配合优势不一样,因此,如何组队成了大问题。
给定n×n优势矩阵P,其中P[i][j]表示男队员i和女队员j进行组队的竞赛优势(0<P[i][j]<10000)。设计一个算法,计算男女队员最佳配对法,使组合出的n支队伍的竞赛优势总和达到最大。
输入格式:
测试数据有多组,处理到文件尾。每组测试数据首先输入1个正整数n(1≤n≤9),接下来输入n行,每行n个数,分别代表优势矩阵P的各个元素。
输出格式:
对于每组测试,在一行上输出n支队伍的竞赛优势总和的最大值。
输入样例:
3
10 2 3
2 3 4
3 4 5
输出样例:
18#include<bits/stdc++.h>
using namespace std;
const long long MOD = 1e9 + 7;
bool judge(string str)
{
string copy_str = str;
reverse(str.begin(),str.end());
return str == copy_str;
}
long long dfs(string str)
{
if (str.size() <= 1) return 1;
long long ans = 0;
for (int i = 0; i < str.size(); ++i)
{
if (judge(str.substr(0, i + 1)))
{
ans = ans + dfs(str.substr(i+1)) % MOD;
ans = ans % MOD;
}
}
return ans;
}
int main()
{
string s;
getline(cin, s);
if (s.empty()) cout << 0 << endl;
else
cout << dfs(s);
return 0;
}
using namespace std;
int n;
int book[101];
int mp[101][101];
int maxsum = 0;
void show() {
for (int i = 1;i < 15;i++)
book[i] = 0;
}
void dfs(int i, int cursum) {
if (i > n) {
if (cursum > maxsum)
maxsum = cursum;
return;
}
for (int j = 1;j <= n;j++) {
if (book[j] == 0 ) {
book[j] = 1;
dfs(i + 1, cursum + mp[i][j]);
book[j] = 0;
}
}
}
int main() {
while (cin >> n) {
for (int i = 1;i <= n;i++) {
for (int j = 1;j <= n;j++) {
cin >> mp[i][j];
}
}
show();
maxsum = 0;
dfs(1, 0);
cout << maxsum<<endl;
}
}
7-4 回文串的切割
分数 20
全屏浏览题目
切换布局
作者 Alan
单位 山东科技大学
Alan觉得回文串是个好东西,可是Alan忘记怎么做了,于是想请你帮帮忙:
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案的个数。
输入格式:
输入一个字符串s
0 ≤ len(s) ≤ 64
输出格式:
输出一个整数代表方案个数。
输入样例:
aab
输出样例:
2
样例解释
所有可能的方案是:
[
["aa","b"],
["a","a","b"]
]
输入样例:
aabccb
输出样例:
6
样例解释
所有可能的方案是:
[
['a', 'a', 'b', 'c', 'c', 'b'],
['a', 'a', 'b', 'cc', 'b'],
['a', 'a', 'bccb'],
['aa', 'b', 'c', 'c', 'b'],
['aa', 'b', 'cc', 'b'],
['aa', 'bccb']
]#include<bits/stdc++.h>
using namespace std;
const long long MOD = 1e9 + 7;
bool judge(string str)
{
string copy_str = str;
reverse(str.begin(),str.end());
return str == copy_str;
}
long long dfs(string str)
{
if (str.size() <= 1) return 1;
long long ans = 0;
for (int i = 0; i < str.size(); ++i)
{
if (judge(str.substr(0, i + 1)))
{
ans = ans + dfs(str.substr(i+1)) % MOD;
ans = ans % MOD;
}
}
return ans;
}
int main()
{
string s;
getline(cin, s);
if (s.empty()) cout << 0 << endl;
else
cout << dfs(s);
return 0;
}
7-5 和谐宿舍
分数 20
全屏浏览题目
切换布局
作者 江太白
单位 江西财经大学
我的某室友学过素描,墙上有n张他的作品。这些作品都是宽度为1,高度不定的矩形,从左到右排成一排,且底边在同一水平线上。
宿舍评比就要来了,为了及格,我们决定买不多于m块的矩形木板,把这些作品和谐掉。要求木板也从左到右排成一排,且底边与作品的底边在同一水平线上。
在能够把所有作品和谐掉的前提下,我们希望这些木板的面积和最小,问最小面积和。
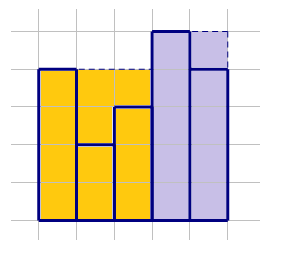
输入格式:
第一行两个数n和m,表示作品数和木板数;
第二行n个数Hi,表示从左到右第i个作品的高度。
输出格式:
一行一个数ans,表示答案。
输入样例:
在这里给出一组输入。例如:
5 2
4 2 3 5 4
输出样例:
在这里给出相应的输出。例如:
22
数据规模和约定
对于30%的数据:1<=n,m<=10;
对于100%的数据:1<=n,m<=100,1<=Hi<=10000。
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int Max = 105;
const int INF = 0X7F7F7F7F; //定义的无穷大
int dp[Max][Max];
int pictureHeight[Max] = { 0 };
int topPicture[Max][Max] = { 0 }; //记录i->j区间内,最高的作品高度
int main() {
int m, n; // m->木板数 n->作品数
memset(dp, INF, sizeof(dp));
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> pictureHeight[i];
for (int i = 1; i <= n; i++)
for (int j = i; j <= n; j++)
topPicture[i][j] = max(topPicture[i][j-1],pictureHeight[j]);
for (int i = 1; i <= n; i++) { //遍历作品
dp[i][1] = i * topPicture[1][i];
for (int j = 2; j <= m; j++) { //遍历木板数
for (int k = 1; k <= i - j + 1; k++) {
dp[i][j] = min(dp[i][j], dp[i - k][j - 1] + k * topPicture[i - k + 1][i]);
}
}
}
cout << dp[n][m];
return 0;
}
7-6 h0221.激光炸弹
分数 17
全屏浏览题目
切换布局
作者 黄正鹏
单位 贵州工程应用技术学院
一种新型的激光炸弹,可以摧毁一个边长为R的正方形内的所有的目标。现在地图上有n(N<=10000)个目标,用整数xi,yi(其值在[0,5000])表示目标在地图上的位置,每个目标都有一个价值。激光炸弹的投放是通过卫星定位的,但其有一个缺点,就是其爆破范围,即那个边长为R的正方形的边必须和x,y轴平行。若目标位于爆破正方形的边上,该目标将不会被摧毁。
输入格式:
第一行为正整数n和正整数R,接下来的n行每行有3个正整数,分别表示xi,yi,wi。
输出格式:
输出文件仅有一个正整数,表示一颗炸弹最多能炸掉地图上总价值为多少的目标(结果不会超过32767)。
输入样例:
在这里给出一组输入。例如:
2 1
0 0 1
1 1 1
输出样例:
在这里给出相应的输出。例如:
1#include<iostream>
using namespace std;
const int N =5010;
int f[N][N];
int n,r;
int main(){
cin>>n>>r;//将目标个数以及爆破边长输入
int xm=r,ym=r;//记录最大的位置,就不用遍历全部位置了,这里要注意的是初始值应该设置成最小的范围正方形,
//这样才能保证下面寻找二维前缀和时的初始访问位置存在
for(int i=1,x,y,w;i<=n;i++)
{
cin>>x>>y>>w;
x++;
y++;//由于要利用前缀和的知识,且本题是有原点存在的即当原点出现时我们需要特判以防数组下标越界
//因此我们直接将全部的点的位置统一向右上移动一个位置那么就不需要特判了
f[x][y]=w;
xm=max(xm,x);
ym=max(ym,y);
}
for(int i=1;i<=xm;i++)
for(int j=1;j<=ym;j++)//求每个点的二维前缀和
{
f[i][j]+=f[i-1][j]+f[i][j-1]-f[i-1][j-1];
}
int sum=0;
for(int i=r;i<=xm;i++)
for(int j=r;j<=ym;j++)
sum=max(sum,f[i][j]-f[i-r][j]-f[i][j-r]+f[i-r][j-r]);
cout<<sum;
return 0;
}
7-1 小H分糖果
分数 20
全屏浏览题目
切换布局
作者 彭昊
单位 吉首大学
小H来到一个小学分糖果,小学生们很听话,站成一排等着分糖果,小H将根据每个人的上次考试分数给一定的糖果,规则如下。
- 每个人都有自己分数ai,代表上次考试成绩。
- 每个人都至少有一颗糖。
- 如果两个人相邻,分数高的一定比分数低的糖果多
然而小H经费有限,他想知道最少需要多少糖果。
输入格式:
输入第一行包括一个整数n(1≤n≤105)。
接下来n行,每行1个整数ai(1≤ai≤105)表示站在第i位的人的分数。
输出格式:
输出最少需要多少糖果
输入样例:
在这里给出一组输入。例如:
3
1
2
2
输出样例:
在这里给出相应的输出。例如:
4#include<bits/stdc++.h>
#define ll long long
#define INF 0x7f7f7f7f //2139062143
#define llINF 9223372036854775807
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
using namespace std;
int n;
int num[100007],cas[100007];
int main()
{
IOS
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>num[i];
cas[i]=0;
}
for(int i=1;i<=n;i++)
{
bool flag=1;
if(i>1&&num[i-1]<num[i]) flag=0;
if(i<n&&num[i+1]<num[i]) flag=0;
if(flag) cas[i]=1;
}
ll ans=0;
for(int i=2;i<=n;i++)
{
if(num[i]>num[i-1]) cas[i]=max(cas[i],cas[i-1]+1);
}
for(int i=n-1;i>0;i--)
{
if(num[i]>num[i+1]) cas[i]=max(cas[i],cas[i+1]+1);
}
for(int i=1;i<=n;i++) ans+=cas[i];
cout<<ans<<endl;
}
7-2 子集和问题
分数 20
全屏浏览题目
切换布局
作者 王东
单位 贵州师范学院
给定n个不同的正整数集合w=(w1,w2,…,wn)和一个正数W,要求找出w的子集s,使该子集中所有元素的和为W。
输入格式:
第一行输入n和W,第二行依次输入n个数。
输出格式:
每行输出一个符合要求的子集。
输入样例1:
4 31
11 13 24 7
输出样例1:
11 13 7
24 7 #include <bits/stdc++.h>
using namespace std;
int n,res;
vector<int> v,v1;
void dfs(int sum,int pos){
if(pos>n) return;
sum += v[pos];
if(sum>res){
return;
}
v1.push_back(v[pos]);
if(sum==res){
for(auto it=v1.begin();it!=v1.end();it++){
cout<<*it<<" ";
}
cout<<endl;
v1.pop_back();
return;
}
for (int i = pos + 1; i <= n;i++){
dfs(sum, i);
}
v1.pop_back();
}
int main(){
cin>>n>>res;
v.resize(n+1);
for(int i=1;i<=n;i++) cin>>v[i];
for(int i=1;i<=n;i++)
dfs(0, i);//从临时和0,数组下标i开始dfs
}
7-3 数列游戏
分数 20
全屏浏览题目
切换布局
作者 谷方明
单位 吉林大学
一个数列有n个整数。每次从中取走一个最长的递增子数列,最少几次能取走全部的数。递增子数列中,相邻两项可以相等。
输入格式:
第1行,一个整数n,表示数列的项数,1≤n≤10000。
第2行,n个整数Ai,用空格分隔,Ai表示数列中第i项,1≤Ai≤1000000,1≤i≤n。
输出格式:
第1行,一个整数,表示第一次取走的最长子数列的项数。
第2行,n个整数,用空格分隔,表示第一次取走的最长子序列。如果有多种选择,输出最靠左的一组。
第3行,一个整数,表示所求最少次数。
输入样例:
在这里给出一组输入。例如:
8
10 9 2 5 3 7 101 18
输出样例:
在这里给出相应的输出。例如:
4
2 5 7 101
4#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> P;
#define INF 0x3f3f3f3f
const int N = 1e4 + 10;
int n;
int dp[N], p[N];
vector<int>a;
void DP()
{
int pos = 0, mx = -1;
for (int i = 0; i < n; i++)
{
dp[i] = 1;
p[i] = i;
for (int j = 0; j < i; j++)
{
if (a[j] <= a[i])
{
if(dp[i] < dp[j] + 1)
{
dp[i] = dp[j] + 1;
p[i] = j;
if (dp[i] > mx)
pos = i;
mx = max(mx, dp[i]);
}
}
}
}
vector<int>s;
while(p[pos] != pos)
{
s.push_back(a[pos]);
pos = p[pos];
}s.push_back(a[pos]);
cout << s.size() << endl;
for (int i = s.size() - 1; i >= 0; i --)
{
if (i != s.size() - 1) cout << " ";
cout << s[i];
}cout << endl;
multiset<int>st;
for(int i = 0;i < n;i ++)
{
multiset<int>::iterator it = st.begin();
if(st.empty()|| a[i] < *it) st.insert(a[i]);
else
{
auto tt = st.upper_bound(a[i]);
tt --;
st.erase(tt);
st.insert(a[i]);
}
}
cout << st.size() <<endl;
}
int main()
{
cin >> n;
int x;
for (int i = 0; i < n; i++)
{
cin >> x;
a.push_back(x);
}
if(n == 1)
cout << 1 <<endl << a[0] << endl << 1;
else
DP();
}
7-4 叠猫猫
分数 20
全屏浏览题目
切换布局
作者 陈英
单位 南昌航空大学
一年一度的叠猫猫活动又来了,这次的叠猫猫邀请别人进组后可以把两个组的人合并。
现在有 n 个人参加这个活动, m 次邀请,每次输出合并后的组员个数。
输入格式:
输入在一行中给出2个正整数 n,m(1<=n,m<=105)。
之后的 m 行,每行输入两个正整数 x,y(1<=x,y<=n) 代表 x 邀请 y 进组
输出格式:
每次邀请后,在一行内输出一个整数代表 y 所在组的总人数。
输入样例:
在这里给出一组输入。例如:
5 4
1 2
3 4
2 3
2 4
输出样例:
在这里给出相应的输出。例如:
2
2
4
4
提示:
20%的数据, 1<=n,m<=10
40%的数据, 1<=n,m<=102
60%的数据,1<=n,m<=104
100%的数据, 1<=n,m<=105
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
const int N = 1e6+10;
int n, m;
int p[N];
int cnt[N];
// 查找祖宗节点
int find1(int x)
{
if(p[x] != x) p[x] = find1(p[x]);
return p[x];
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++ ) p[i] = i, cnt[i] = 1;
while(m -- )
{
int x, y;
scanf("%d %d",&x, &y);
if(find1(x) != find1(y)) cnt[find1(x)] += cnt[find1(y)];
p[find1(y)] = find1(x);
cout << cnt[find1(x)] << endl;
}
return 0;
}7-5 范围和
分数 20
全屏浏览题目
切换布局
作者 Drizzle
单位 山东科技大学
给你一个整数数组 nums 。nums 中,子数组的 范围 是子数组中最大元素和最小元素的差值。
返回 nums 中 所有 子数组范围的 和 。
子数组是数组中一个连续 非空 的元素序列。
示例 1:
输入:
3
1 2 3
输出:
4
- 解释:nums 的 6 个子数组如下所示:
[1],范围 = 最大 - 最小 = 1 - 1 = 0
[2],范围 = 2 - 2 = 0
[3],范围 = 3 - 3 = 0
[1,2],范围 = 2 - 1 = 1
[2,3],范围 = 3 - 2 = 1
[1,2,3],范围 = 3 - 1 = 2
所有范围的和是 0 + 0 + 0 + 1 + 1 + 2 = 4
提示:
- 1 <= nums.length <= 1000
- −109 <= nums[i] <= 109
进阶:你可以设计一种时间复杂度为 O(n) 的解决方案吗
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1010;
int num[N];
int n;
int main()
{
cin >> n;
for (int i=0;i<n;i++) cin >> num[i];
ll ans = 0;
for(int i=0;i<n;i++)
{
int mx = INT_MIN,mn = INT_MAX;
for(int j=i;j<n;j++)
{
mx = max(mx,num[j]);
mn = min(mn,num[j]);
ans += mx - mn;
}
}
cout << ans;
}
7-6 ACM宣传
分数 20
全屏浏览题目
切换布局
作者 杜祥军
单位 青岛大学
LB大神想组织集训队去学校各处宣传ACM,但是大神不想让队员们走太多路,因此想写代码计算一下,到各地宣传再回到博知401的最短路径总和是多少。
已知:学校一共有n个宣传点,博知401是标号为1的点。剩下n-1个点每个点各派1位队员,询问每个队员到达宣传点再回到博知401的最短路径和是多少。
输入格式:
输入由T个案例组成。输入的第一行只包含正整数T。
接下来是N和M,1 <= N,M <= 1000000,表示N个点和连接N个点的M条边。
然后有M行,每行包括三个值U,V,W,表示从点U到点V需要W的路程。你可以假设该图连通。
输出格式:
对于每个案例,打印一行,表示队员们从博知401出发到其他点再回到博知401的路径总和的最小值。
输入样例:
2
2 2
1 2 13
2 1 33
4 6
1 2 10
2 1 60
1 3 20
3 4 10
2 4 5
4 1 50
输出样例:
46
210#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> P;
#define INF 0x3f3f3f3f
const int N = 1e6 + 10;
int n, m;
struct node
{
int v,w;
node(int vv,int ww):v(vv),w(ww){}
};
vector<node>e[2][N];
int dis[2][N];
bool vis[N];
void dijkstra(int t)
{
memset(vis,0,sizeof(vis));
priority_queue<P,vector<P>,greater<P> >q;
for(int i=2;i<=n;i++) dis[t][i] = INF;
q.push(P(dis[t][1],1));
while (!q.empty())
{
P tp = q.top();
q.pop();
int u = tp.second;
if(vis[u]) continue;
vis[u] = true;
for(int i=0;i<e[t][u].size();i++)
{
int v = e[t][u][i].v;
int w = e[t][u][i].w;
if(dis[t][u] + w < dis[t][v])
{
dis[t][v] = dis[t][u] + w;
q.push(P(dis[t][v],v));
}
}
}
}
int main()
{
int T,x,y,z;
cin >> T;
while (T --)
{
memset(e,0,sizeof(e));
cin >> n >> m;
while (m --)
{
cin >> x >> y >> z;
e[0][x].push_back(node(y,z));
e[1][y].push_back(node(x,z));
}
dijkstra(0);
dijkstra(1);
ll ans = 0;
for(int i=2;i<=n;i++)
ans += dis[0][i] + dis[1][i];
cout << ans <<endl;
}
}