接上一篇文章http://t.csdnimg.cn/nsKsW,本次我们接着讲解关于二叉树的相关知识。
一、二叉树的相关性质:
1. 若规定根节点的层数为 1 ,则一棵非空二叉树的 第 i 层上最多有 2^(i-1) 个结点.2. 若规定根节点的层数为 1 ,则 深度为 h 的二叉树的最大结点数是 2^(h-1)3. 对任何一棵二叉树 , 如果度为 0 其叶结点个数为n0 , 度为 2 的分支结点个数为n1 , 则有n0=n1+14. 若规定根节点的层数为 1 ,具有 n 个结点的满二叉树的深度,h= 5. 对于具有 n 个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从 0 开始编号,则对于序号为i 的结点有:①. 若 i>0 , i 位置节点的双亲序号为: (i-1)/2 ; i=0; 若 i 为根节点编号,无双亲节点②. 若 2i+1<n ,左孩子序号: 2i+1; 2i+1>=n 否则无左孩子③. 若 2i+2<n ,右孩子序号: 2i+2; 2i+2>=n 否则无右孩子6.通过孩子找双亲:设孩子的编号为i,则其双亲的编号为A=(i-1)/2;根节点没有双亲;
5. 对于具有 n 个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从 0 开始编号,则对于序号为i 的结点有:①. 若 i>0 , i 位置节点的双亲序号为: (i-1)/2 ; i=0; 若 i 为根节点编号,无双亲节点②. 若 2i+1<n ,左孩子序号: 2i+1; 2i+1>=n 否则无左孩子③. 若 2i+2<n ,右孩子序号: 2i+2; 2i+2>=n 否则无右孩子6.通过孩子找双亲:设孩子的编号为i,则其双亲的编号为A=(i-1)/2;根节点没有双亲;
二、二叉树的存储结构:
(一)、顺序储存(数组)
1.顺序结构存储就是使用 数组来存储 ,一般使用数组 只适合表示完全二叉树 ,因为不是完全二叉树会有空间的浪费。而现实中使用中只有 堆 才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺 序存储在物理上是一个数组,在逻辑上是一颗二叉树。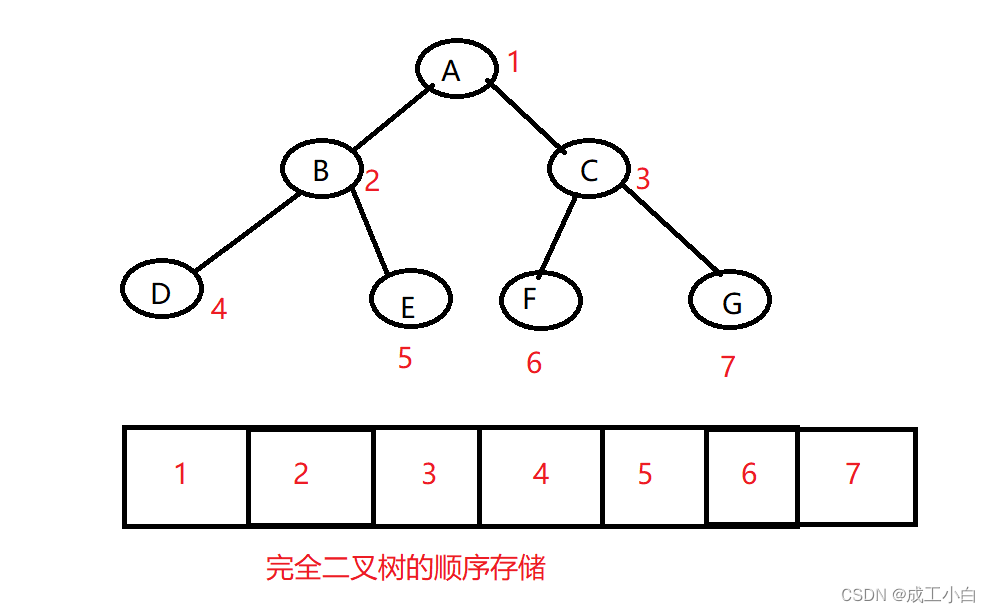 根据上述有几点性质:2. 对于具有 n 个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从 0 开始编号,则对于序号为i 的结点有:①. 若 i>0 , i 位置节点的双亲序号为: (i-1)/2 ; i=0; 若 i 为根节点编号,无双亲节点②. 若 2i+1<n ,左孩子序号: 2i+1; 2i+1>=n 否则无左孩子③. 若 2i+2<n ,右孩子序号: 2i+2; 2i+2>=n 否则无右孩子3.通过孩子找双亲:设孩子的编号为i,则其双亲的编号为A=(i-1)/2;根节点没有双亲;4.满二叉树或者完全二叉树适合用顺序存储,而非完全二叉树适合用链式存储;
根据上述有几点性质:2. 对于具有 n 个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从 0 开始编号,则对于序号为i 的结点有:①. 若 i>0 , i 位置节点的双亲序号为: (i-1)/2 ; i=0; 若 i 为根节点编号,无双亲节点②. 若 2i+1<n ,左孩子序号: 2i+1; 2i+1>=n 否则无左孩子③. 若 2i+2<n ,右孩子序号: 2i+2; 2i+2>=n 否则无右孩子3.通过孩子找双亲:设孩子的编号为i,则其双亲的编号为A=(i-1)/2;根节点没有双亲;4.满二叉树或者完全二叉树适合用顺序存储,而非完全二叉树适合用链式存储;
(二)、衍生数据结构——堆:
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆 ( 一种二叉树 ) 使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
1.堆的概念
堆是一种非线性结构,是特殊的完全二叉树,所以适合用数组存储;
2.堆的分类:
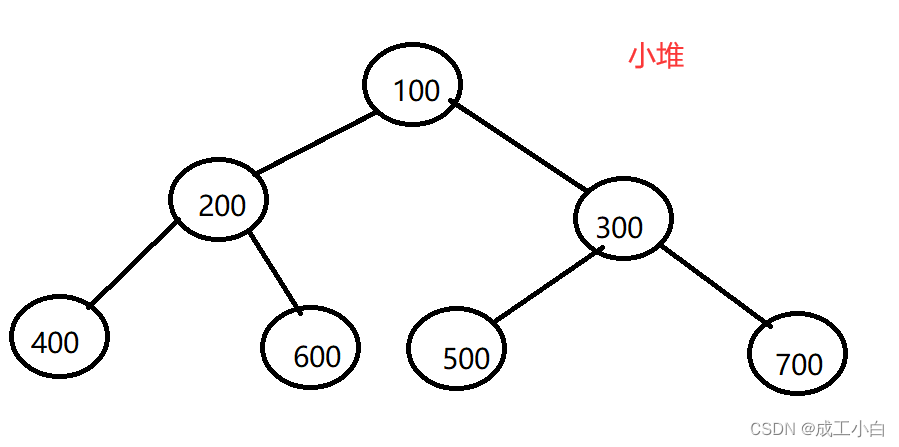
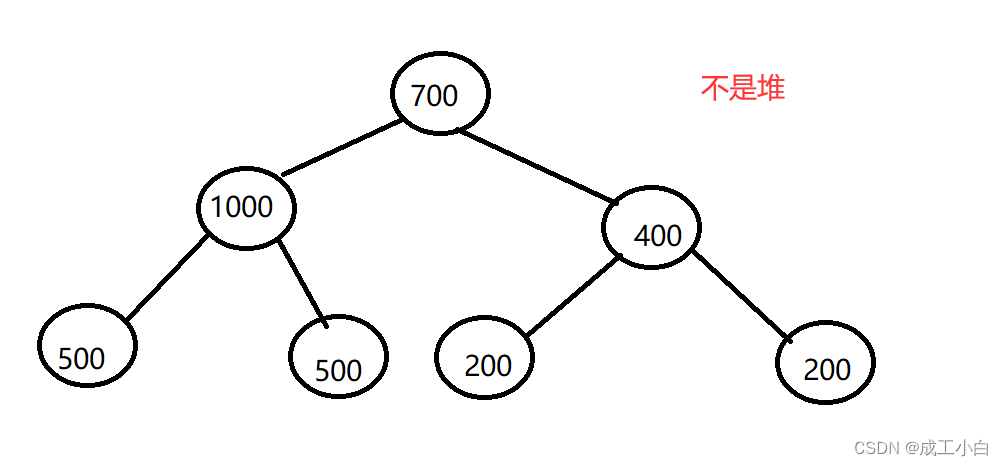
小堆(小根堆):树中任意父亲的值都小于等于其孩子;
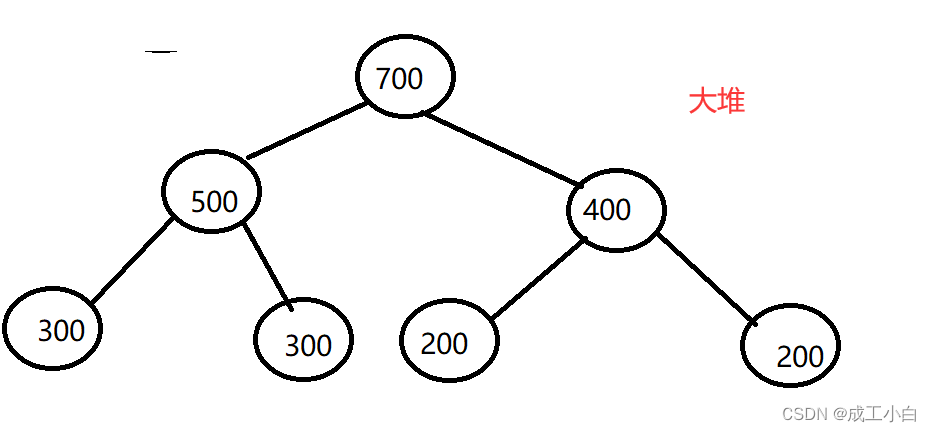
大堆(大根堆):树中任意父亲的值都大于等于其孩子;
如下图:
(三)、堆的实现(顺序存储)
一般堆我们用顺序存储的方式实现,即用一维数组,所以定义与顺序表差不多,只是实现逻辑不一样,所以基本定义与销毁等操作就大致讲解。
1.堆的定义:
typedef int HPDatatype; typedef struct Heap { HPDatatype* a;//一维数组 int size;//现有元素个数 int capacity;//当前结构最大空间 }HP;
2.堆的初始化:
//初始化 void HPinit(HP* php) { assert(php); php->size = 0; php->capacity = 0; php->a = NULL; }
3.堆的销毁
//销毁 void HPDestroy(HP* php) { assert(php); free(php->a); php->a = NULL; php->size = 0; php->capacity = 0; }
4.堆的打印:
//打印 void HPprint(HP* php) { assert(php); for (int i = 0; i < php->size; i++) { printf("%d ", php->a[i]); } printf("\n"); }
5.插入数据:
因为堆是特殊的完全二叉树,所以插入算法与顺序表完全不同;
我们以实现小堆为例:
①:首先我们应该考虑是否堆满,根据我们定义所示,当size==capacity时即为堆满,此时我们需要进行扩容方式,因为只有此处可能进行扩容,所以不用单独分装成一个函数,扩容方式与之前的顺序表等等结构相似,所以小编不做多余讲解;
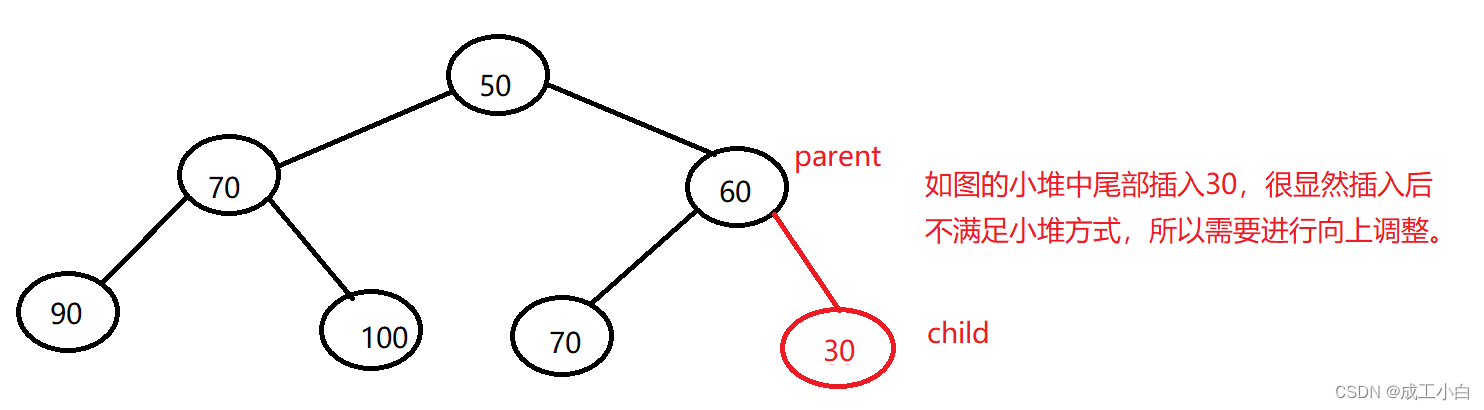
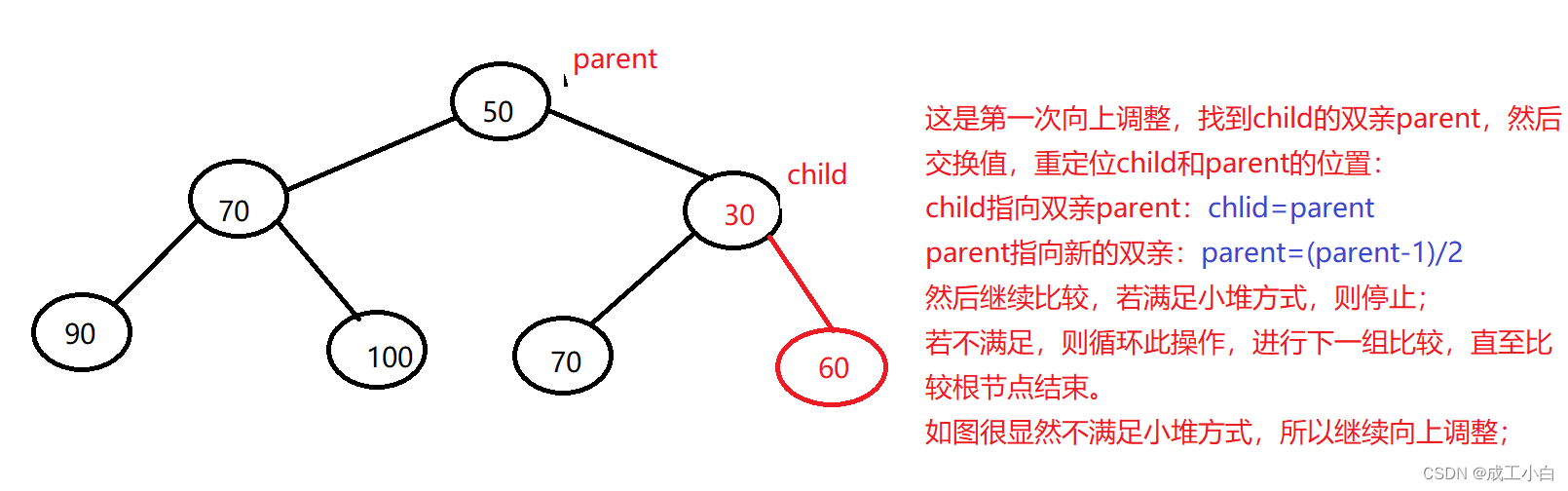
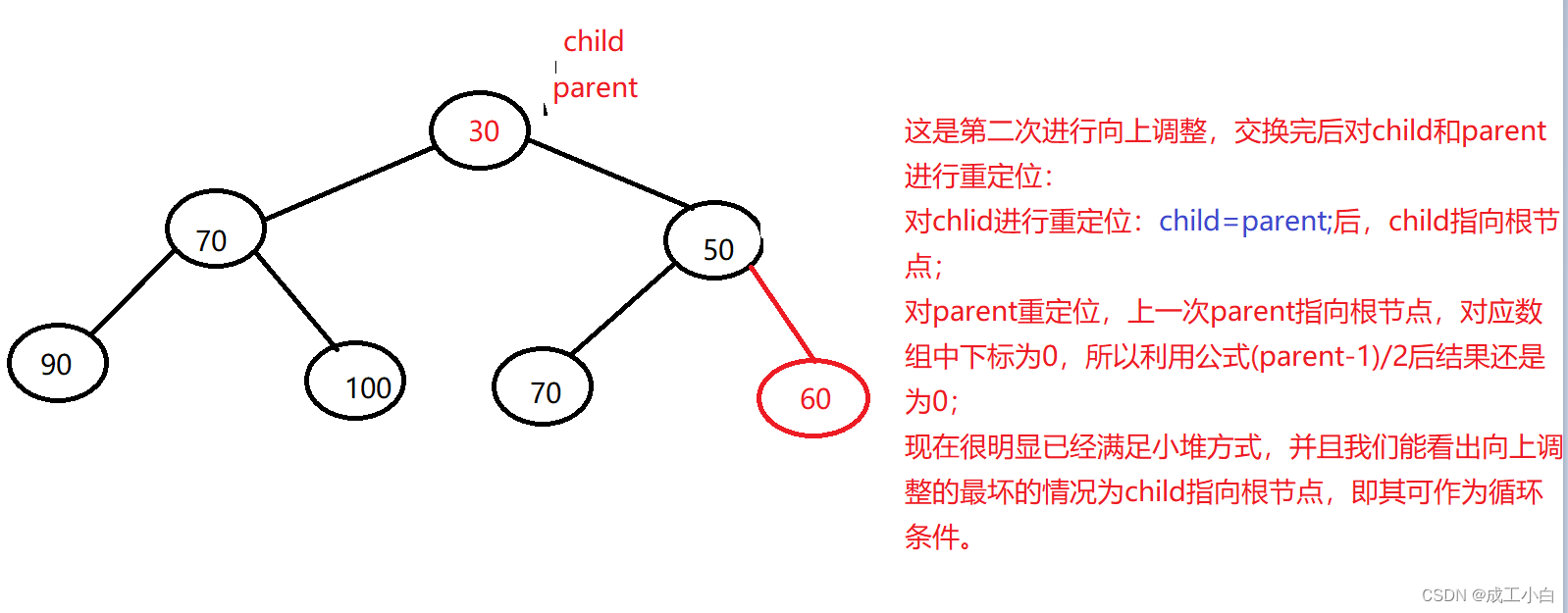
②:根据完全二叉树的顺序存储结构来看,我们知道数组的尾元素即为完全二叉树的尾元素,所以我们插入数据只需在数组的尾部进行插入,又因为堆是特殊的完全二叉树,小堆即双亲结点的值比其所有孩子的值要小,所以当数据插入后,还要将数据与其双亲进行比较,若不满足条件,我们要进行数据的交换,而且我们需要循环进行此操作,直到比较完根节点,又因为我们是不断在找双亲,所以我们称这种方法为“向上调整”,向上调整的前提是前面的结构已经是堆结构了。
③:我们既然要找双亲,所以我们需要牢记双亲结点与孩子结点之前的位置关系,即为上述的几条完全二叉树的性质,向上调整具体算法如下图:
④:时间复杂度为O(log以2为底的n),因为插入元素的时间复杂度为O(1),向上调整的最坏情况为调整至根结点,即完全二叉树的高度,为log以2为底的n;
⑤,源代码
//交换函数 void Swap(HPDatatype* p1, HPDatatype* p2) { HPDatatype tmp = *p1; *p1 = *p2; *p2 = tmp; } //向上调整 void AdjustUp(HPDatatype* a, int child) { int parent = (child - 1) / 2; while (child > 0) { //以小堆为例插入数据 if (a[parent] > a[child]) { //交换位置 Swap(&a[parent],&a[child]); //比较完一组后重定位,向上调整 child = parent; parent = (parent - 1) / 2; } else { //插入结束 break; } } } //插入元素 void HPPush(HP* php, HPDatatype x) { assert(php); //扩容 if (php->size == php->capacity) { php->capacity = (php->capacity == 0 ? 4 : php->capacity * 2); HPDatatype* tmp = (HPDatatype*)realloc(php->a, sizeof(HPDatatype) * php->capacity); //检查扩容 if (tmp == NULL) { perror("realloc"); return; } php->a = tmp; } //插入元素 php->a[php->size] = x; //检查是否需要向上调整 AdjustUp(php->a, php->size); php->size++; }
6.删除数据:
首先我们考虑一个问题,删除哪个元素有意义呐?
很明显,删除根节点最有意义,因为在大堆中,根节点是最大值;在小堆中,根节点是最小值;所以删除根节点比较有意义一些;
很多小伙伴可能会想,“删除根结点无非就是将数组元素挪动直接覆盖嘛”,答案是不行的,因为我们要清楚一点,堆结构只是孩子与双亲有关系,但孩子之间和兄弟之间是没有关系的,所以挪动数据覆盖元素可能会导致孩子或者兄弟错位,从而覆盖后可能就不是堆结构了;
下面介绍一种思路:上面插入数据用到“向上调整”,现在我们删除数据就用到“向下调整”;
向下调整思路(以小堆结构为例):
①:先交换根结点和尾结点的值;
②:删除尾结点(数组总元素size减1)
③:再找出根结点的两个孩子中较小的孩子,然后交换双亲与较小孩子的值;
④:接着对双亲和孩子重定位,依次向下调整;
注意:其中很多细节应当尤其注意,如可能有些情况没有右孩子等等,具体思路看注释;
//向下调整 void AdjustDown(HPDatatype* a, int n, int parent) { int child = parent * 2 + 1; while (child<n) { //找出小孩子,同时要注意有没有右孩子,防止child+1越界 if (a[child] > a[child + 1]&&child+1<n) { child++; } //交换 if (a[child] < a[parent]) { Swap(&a[child], &a[parent]); //继续向下调整 parent = child; child = parent * 2 + 1; } else { break; } } } //删除元素 void HPPop(HP* php) { assert(php); //判断堆空 assert(php->size > 0); //交换首尾结点 Swap(&php->a[0], &php->a[php->size - 1]); //删除尾结点,因为是数组,所以直接将现有元素size-1不访问即可 --php->size; //向下调整 AdjustDown(php->a, php->size, 0); }
7.取堆顶元素(取根节点)
//取堆顶(取根结点) HPDatatype HPTop(HP* php) { assert(php); //判断是否为堆空 assert(php->size > 0); return php->a[0]; }
8.判空
//判空 bool HPEmpty(HP* php) { assert(php); return php->size == 0; }
本文章未完待续