题目：

1212. 地宫取宝 - AcWing题库

 

 思路：dp（最长上升子序列和摘花生的结合）

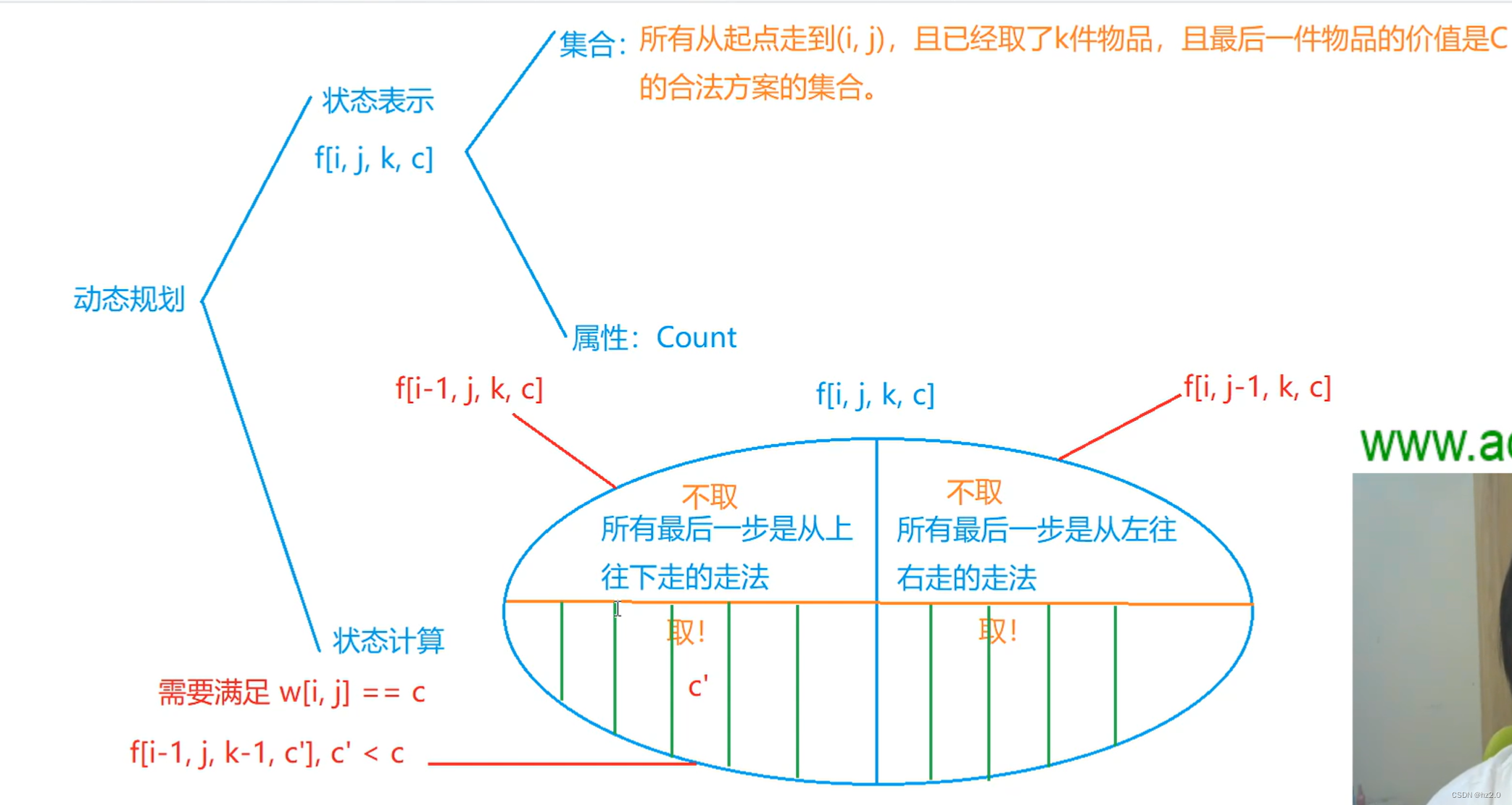
代码：

 

#include<iostream>
using namespace std;
const int N = 55;
const int MOD = 1000000007;

int n, m, k;
int w[N][N];//每个坐标格子上宝贝的价值

int f[N][N][13][14];/*f是当前条件下的方案数量。
前两维表示坐标
三维表示已经取得的宝贝数量
四维表示已经取得的宝贝中的最后一个宝贝的价值（即当前最大）*/

int main()
{
	//输入行n列m以及所需要的宝贝数量k
	cin >> n >> m >> k;

	//输入每个格子宝贝的价值
	for(int i=1;i<=n;i++)
		for (int j = 1; j <= m; j++) {
			cin >> w[i][j];
			w[i][j]++;//为方便对f进行初始化，将每个宝贝的价值都加一，不影响结果
		}

	//f初始化
	f[1][1][0][0] = 1;//起点，不拿起点坐标格子上的宝贝
	/*此时没有取任何一件宝贝，故存入的最大值为空，应该比所以宝贝的价值都小。
	宝贝原本的最小值为0，但下标不能取负数，这也是为何上面要将宝贝的整体价值加一的原因*/
	f[1][1][1][w[1][1]] = 1;//起点，拿起点坐标格子上的宝贝
	
	for(int i=1;i<=n;i++)//一维横坐标
		for (int j = 1; j <= m; j++) {//二维纵坐标
			if (i == 1 && j == 1)continue;//f的第一行第一列已经初始化过了

			for(int u=0;u<=k;u++)//三维表示已经取得宝贝数量
				for (int v = 0; v <= 13; v++)//四维表示已取得宝贝的最大价值
				{
					//不取当前空格的宝贝
					f[i][j][u][v] = (f[i][j][u][v] + f[i - 1][j][u][v]) % MOD;//存图左上角
					f[i][j][u][v] = (f[i][j][u][v] + f[i][j - 1][u][v]) % MOD;//存图左上角

					//取当前空格的宝贝
					if (u > 0 && v == w[i][j])//此时当前格子上的宝贝的价值为最大v
					{
						for (int c = 0; c < v; c++)
						{
							f[i][j][u][v] = (f[i][j][u][v] + f[i - 1][j][u - 1][c]) % MOD;//图左下
							f[i][j][u][v] = (f[i][j][u][v] + f[i][j - 1][u - 1][c]) % MOD;//图右下
						}
					}
				}
		}
	int res = 0;//累加器，求到达右下角(m,n)时所以取得宝贝数量为k且满足递增条件的情况
	for (int i = 0; i <= 13; i++)res = (res + f[n][m][k][i]) % MOD;
	cout << res << endl;

}