近年来强化学习算法广泛应用于游戏对抗上,通用的强化学习模型一般包含了Actor模型和Critic模型,其中Actor模型根据状态生成下一步动作,而Critic模型估计状态的价值,这两个模型通过相互迭代训练(该过程称为Generalized Policy Iteration GPI过程),最终将收敛到某个近优的点。
但对于围棋游戏来说,早些年很多人作为通过计算机来战胜人类顶尖棋手是不可能的,因为围棋总共下法大概在范围,比可观测宇宙的原子数目都要大很多,如此巨大的状态空间和动作空间,通过传统的强化学习方法来进行探索几乎是不可能的。
早期Alphago所采用方法是先通过监督学习专家决策序列,然后再通过强化学习策略来优化。而Alphago Zero是Alphago的升级版,它完全依赖自我对弈的强化学习,无需人类专家的动作监督。
Alphago Zero通过采用MCTS策略,从大量的动作空间中搜索当前最优的动作序列,然后让模型根据这些最优动作序列进行训练,不需要先监督学习专家决策,就能通过自我学习达成最优的效果。
Alphago Zero的训练主要分为了self-play、训练网络和网络评估三个阶段:
1. self-play阶段
在self-play阶段,采用了一种高效样本探索策略MCTS(Monte Carlo Tree Search),其从庞大的动作空间中寻找出当前最优的动作序列,并将其作为后续强化模型训练的优质样本。通过这种方式,MCTS能够在大规模、复杂的环境中做出明智且有效的决策,并帮忙逐步优化强化模型的学习。
在每轮self-play过程中,都会通过MCTS策略采样生成一系列的游戏轮数,每轮游戏都是指游戏结束(直接出现获胜者)或者游戏步数达到设定最大值(以当前游戏得分判定获胜者)。
每轮游戏都包含围棋双方在整轮过程全部(状态State、动作Action、价值Value)元组,其都是根据MCTS策略进行决策和计算的。每轮游戏在开始前,会构建一个搜索树,然后依次根据当前状态决策动作,具体决策动作方式:
在每轮self-play过程中,通过MCTS策略进行采样,生成一系列的游戏轮次。每轮游戏以两种方式结束:一是游戏直接出现获胜者,二是游戏步数达到设定的最大值,此时根据当前游戏得分判定获胜者。
每轮游戏都会记录下围棋双方的完整过程,包括每步中状态State、动作Action和价值Value等信息,这些数据都是基于MCTS策略进行决策和计算的。
-
状态State:这是围棋的当前局面,包括棋盘上的黑白棋子布局、提子情况等。
-
动作Action:这是围棋的下一步行动(如落子在棋盘的某个位置)。
-
价值Value:当前状态下的获胜概率
每轮游戏在开始之前会构建一个搜索树,然后根据当前状态依次决策动作。具体决策动作的方式如下:
- 动作选择概率
计算,其中
是归一化因子,
是温度控制的超参数,可以随着本轮动作进行,会越趋向于选择概率最大的动作。
的计算逻辑:
- 如果
已经在搜索树中,即该轮游戏已经探索。
- 选择最优的动作,此时为
的一次访问
是一个平衡先验后验动作概率的超参数。
-
表示当前状态-动作的价值估计累计值,
表示从
继续探索直到遇到一个未探索的结点,
表示当未探索结点为对手状态时取负号,否则为正号。
-
表示当前状态-动作在本轮游戏的访问次数,每轮访问后$+1$
-
表示当前状态的本轮游戏的访问次数
-
-
表示归一化的模型先验预估动作概率
- 选择最优的动作,此时为
-
如果
不在搜索树中,即未被探索。
-
通过模型求解
、
,并返回。
-
-
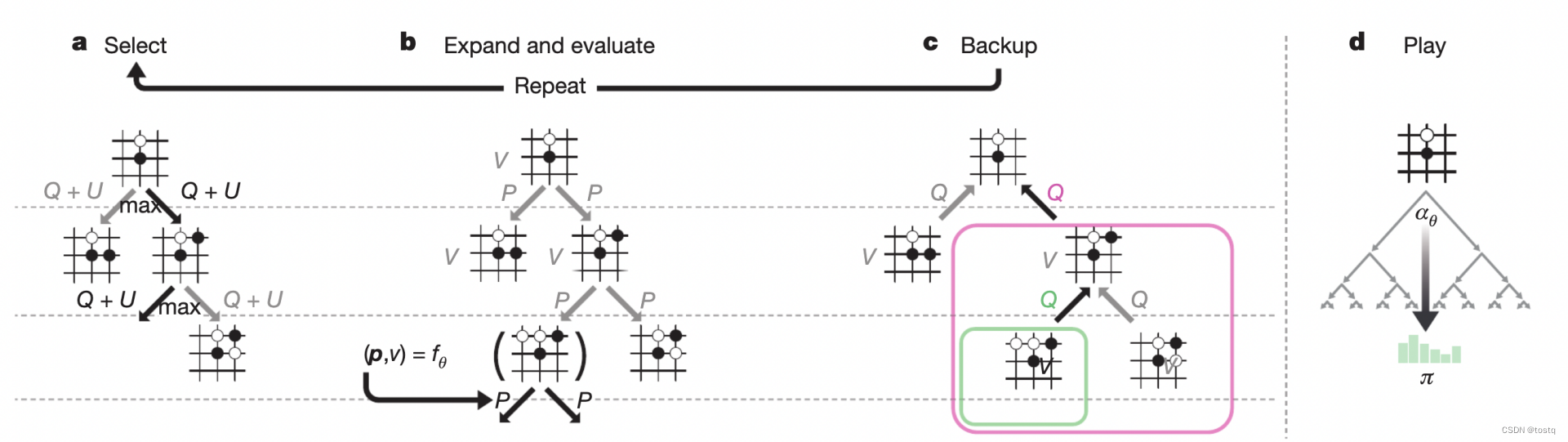
上述过程也可以用select、expand、Backup、play四个阶段来表示:
- Select:表示选择最优的动作
- Expand:表示在选择最优动作后,一直继续探索直到一个未探索的结点,通过模型预估其先验动作概率
及状态价值
,如果是中途遇到已探索的结点,通过Select选择最优的动作。
- Backup:表示在探索直到一个未探索的结点后,沿路径更新树上各状态结点的
、
- Play:该轮游戏采样并确定动作,进入下一状态。
- Select:表示选择最优的动作
2. 训练网络阶段
经过每轮self-play后,会生成一系列的游戏轮数,每轮游戏都会保存正反双方在每步的状态、动作概率
、价值
,作为此轮网络训练阶段的数据,其中:
-
表示当前状态
所属棋方最终是否胜出,其值为
,分别表示负平胜。
-
表示根据该轮游戏在过程中的双方的得分数归一化的值。
-
表示该轮游戏总共的走子数,该项主要是为了平衡初始开局的噪声。
最终loss包含了三个部分:动作分类交叉熵损失、价值预估的MSE损失、参数正则项
3. 网络评估阶段
该阶段主要判断上述经过新一轮训练后的新模型是否是最优,如果是最优的替换最优模型进入下一轮的self-play阶段。
评估最优的方式同self-play阶段是类似的,每一步动作都是还需要通过MCTS策略来进行决策。只不过正反双方分别基于基线模型和更新模型来进行比较。
4. 特征组织形式

-
状态
的维度为
,其中
表示围棋棋盘的二维结构,并在第3维叠加黑白双方在过去8步的位置信息,另外为了区分当前走子是黑子还是白子,增加了一维来标识。
-
动作
的维度为
,表示在
棋盘中下子的位置以及不走子的动作。在实际决策动作时,会直接将不合法的动作概率置为0。
5. 模型结构
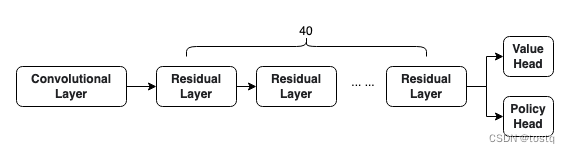
-
输入卷积层:

-
残差模块层

-
policy层

-
value层






![[动态规划] (十四) 简单多状态 LeetCode LCR 091.粉刷房子](https://img-blog.csdnimg.cn/img_convert/f67a4ae3724bf6776b5fe0243422260e.png)