一、中国剩余定理的弊端

在第二十九章中，作者详细地讲解了中国剩余定理的使用，在开始本章节的讲解之前，建议读者先去看上一章节的讲解。传送门：中国剩余定理与线性同余方程组

中国剩余定理是用来解决线性同余方程组的，但是有一个很苛刻的要求就是：方程组中的同余方程的模数必须是互质的。只有这样我们才能套用中国剩余定理。

二、扩展中国剩余定理

1、作用

扩展中国剩余定理就是为了解决方程组中模数不互质的情况。

2、内容

$$\{\begin{array}{l}x\equiv a_{1}mod(m_1)\\ x\equiv a_{2}mod(m_2)\\ x\equiv a_{3}mod(m_3)\\ ...\\ x\equiv a_{n}mod(m_n)\end{array}$$
我们取出前两个式子：

$$\begin{gathered} x\equiv a_{1}mod(m_1) \\ x\equiv a_{2}mod(m_2) \end{gathered}$$

这两个式子能够写成：
$$\begin{gathered} x=k_1{m}_1+a_1 \\ x=k_2{m}_2+a_2 \end{gathered}$$
两个式子相减：
$$k_1{m}_1+a_1=k_2{m}_2+a_2$$
将上面的式子移项：
$$k_1{m}_1-k_2{m}_2=a_2-a_1$$

我们把$k_1$和$-k_2$看作$x_k$和$y_k$。

那么这个式子就可以写成：
$$x_k{m}_1+y_k{m}_2=(a_2-a_1)$$

根据我们的裴蜀定理：

如果$gcd(m_1,m_2)|(a_2-a_1)$

我们就能够根据扩展欧几里德算法计算出系数。

如果上述整除的关系不成立，说明这个式子是无解的。

我们现在来讨论整除关系成立的情况：

我们可以根据欧几里得算法计算出：

$$x_0{m}_1+y_0{m}_2=gcd(m1,m2)$$的特殊解。

为了得到我们的$x_k$和$y_k$，我们需要给两遍同乘$\frac{(a_2-a_1)}{gcd(m_1,m_2)}$

所以我们的$x$和$y$的特殊解可以写成：

$$\begin{gathered} x_{k1}=x_0\ast \frac{(a_2-a_1)}{gcd(m_1,m_2)} \\ {y}_{k1}=y_0\ast \frac{(a_2-a_1)}{gcd(m_1,m_2)} \end{gathered}$$

但是这是一组特殊解：

当我们式子为：

$$x_0{m}_1+y_0{m}_2=n\ast gcd(m1,m2)$$

此时我们可以通过特殊解构造出一般解：

我们构造的原则是下面的等式恒成立：

$x_0{m}_1+y_0{m}_2=gcd(m1,m2)$

因此我们给我们的特殊解进行如下变形：

$$\begin{gathered} x_k=x_{k1}+\frac{m_2}{gcd(m_1,m_2)}\ast n \\ {y}_k=y_{k1}-\frac{m_1}{gcd(m_1,m_2)}\ast n \end{gathered}$$

我们将这两个式子带回：$$x_0{m}_1+y_0{m}_2=gcd(m1,m2)$$

发现依然是成立的。

所以我们构造的$x_k$和$y_k$就是通解。

此时带回我们的
$$x=k_1{m}_1+a_1$$
我们前面是将$k_1$看作了$x_k$，所以我们的式子可以变形为：
$$x=\frac{m_2\ast m_1}{gcd(m_1,m_2)}\ast n+x_{k1}\ast m_1+a_1$$

而$\frac{m_2\ast m_1}{gcd(m_1,m_2)}$就是我们的最小公倍数。因为：

$最大公因数\ast 最小公倍数=两个数的乘积$

所以我们让：

$$lcm(m_1,m_2)=\frac{m_2\ast m_1}{gcd(m_1,m_2)}$$

所以我们的式子可以化简为：
$$x=lcm(m_1,m_2)\ast n+x_{k1}{m}_1+a_1$$

而这个式子可以写成：

$$x\equiv r(modm)$$

其中：

$$\{\begin{array}{l}r=k_1{m}_1+a_1\\ m=lcm(m_1,m_2)\end{array}$$

经过上述推导，我们将两个同余方程：

$$\begin{gathered} x=k_1{m}_1+a_1 \\ x=k_2{m}_2+a_2 \end{gathered}$$

合并成了一个同余方程：

$$x\equiv r(modm)$$

因此，我们只需要不断地去合并，经过$n-1$次合并，我们就能够把$n$个同余方程合并成一个同余方程。

当只有一个合并方程的时候，我们肯定就能够利用扩展欧几里得算法进行计算了。

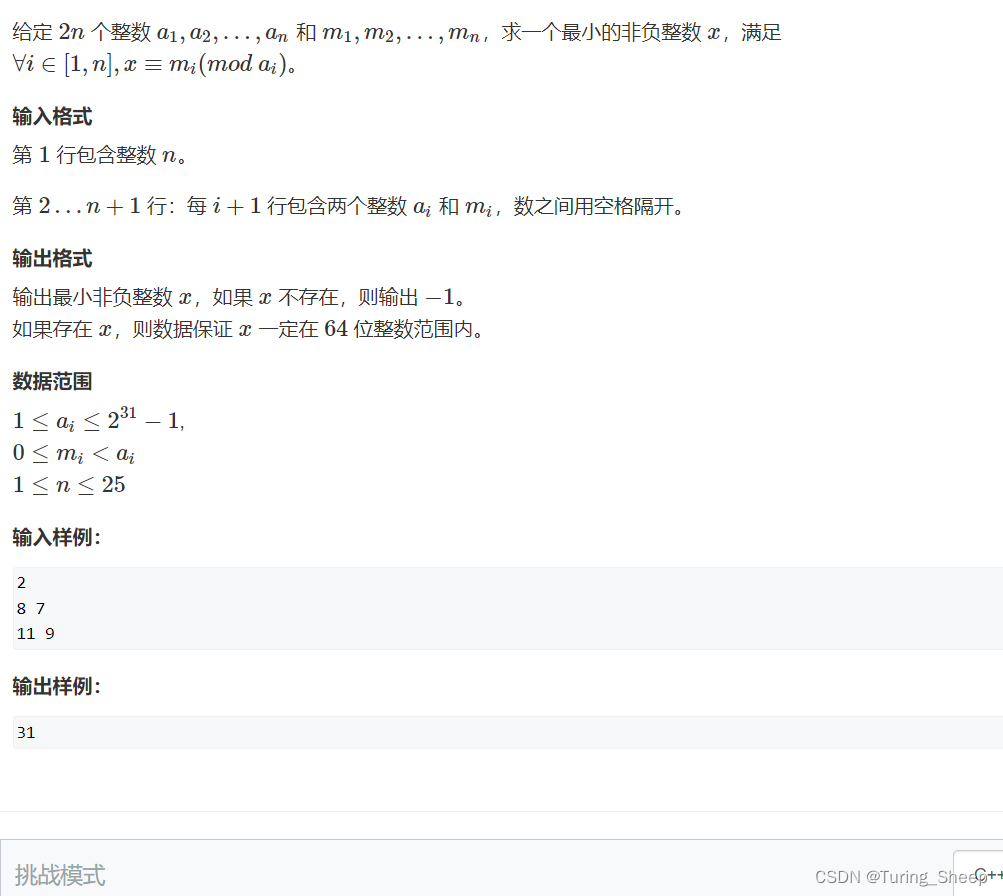
3、问题

4、代码

#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
LL exgcd(LL a, LL b, LL &x, LL &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    LL d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}
int main()
{
    int n;
    cin >> n;
    LL x = 0, m1, a1;
    cin >> m1 >> a1;
    for (int i = 0; i < n - 1; i ++ )
    {
        LL m2, a2;
        cin >> m2 >> a2;
        LL k1, k2;
        LL d = exgcd(m1, m2, k1, k2);
        if ((a2 - a1) % d)
        {
            x = -1;
            break;
        }
        k1 *= (a2 - a1) / d;
        k1 = (k1 % (m2/d) + m2/d) % (m2/d);
        x = k1 * m1 + a1;
        LL m = abs(m1 / d * m2);
        a1 = k1 * m1 + a1;
        m1 = m;
    }
    if (x != -1) x = (a1 % m1 + m1) % m1;
    cout << x << endl;
    return 0;
}