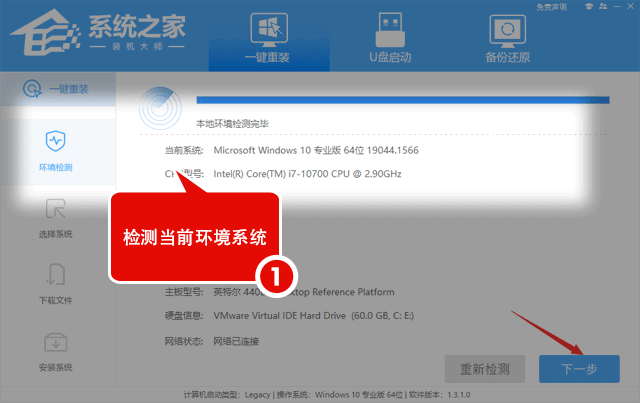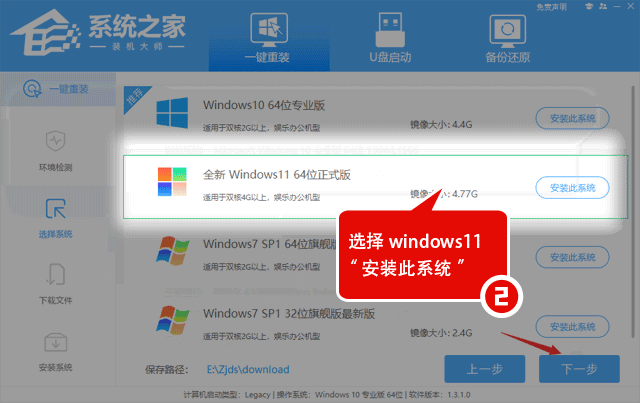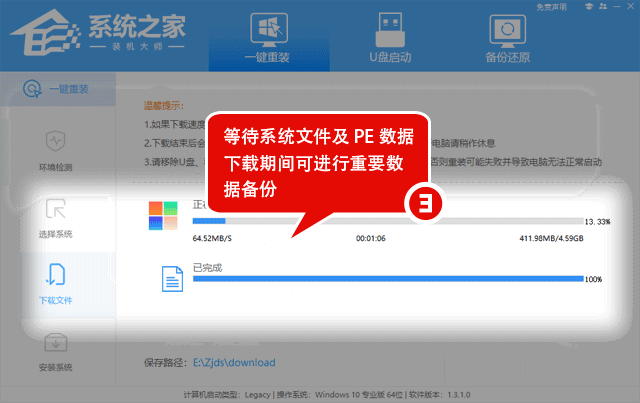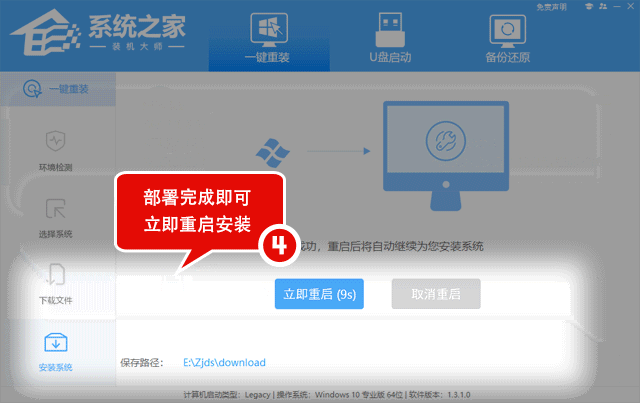
1. 单调栈

• 应用场景：求解下一个更大/小的数
• 原理：空间换时间，暴力解法O（n）
• 单调栈作用：记录遍历过的元素，与当前元素进行对比

模板:求解左边比它更小的元素

单调递增的栈（底——》顶）

//单调递增的栈
import java.util.*;
class Main{
    static int N=100010;
    static int[] a=new int[N];
    static int[] res=new int[N];
    public static void main(String[] args){
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt();
        for(int i=0;i<n;i++)a[i]=sc.nextInt();
        ArrayDeque<Integer> q=new ArrayDeque<>();
        for(int i=0;i<n;i++){
            while(!q.isEmpty() && a[i]<=q.peek())q.pop();
            if(q.isEmpty())res[i]=-1;
            else res[i]=q.peek();
            q.push(a[i]);
        }
        for(int i=0;i<n;i++)System.out.print(res[i]+" ");
        
    }
    
}

• 如果求解右边比他更小的元素，可以倒着遍历
• 如果是更大，则修改为单调递减的栈，也就是修改a[i]<=q.peek()
• 栈中存放下标/元素：取决于是否需要计算宽度（坐标差）
• =:具体情况具体分析

快速记忆

• 单调减栈：比栈顶元素小，直接入栈
• 单调增：比栈顶元素大：直接入栈

2.实战分析

• 分析可知，这是要求右边比他更大的元素
• 所以：倒序遍历，单调递减栈

class Solution {
    //求解右边第一个比他大的元素
    //计算宽度，所以存储下标
    public int[] dailyTemperatures(int[] t) {
        int n=t.length;
        int[] res=new int[n];
        ArrayDeque<Integer> sta=new ArrayDeque<>();
        for(int i=n-1;i>=0;i--){//倒序遍历
            while(!sta.isEmpty() && t[i]>=t[sta.peek()])sta.pop();//单调递减栈
            if(sta.isEmpty())res[i]=0;//为空时赋得值
            else res[i]=sta.peek()-i;
            sta.push(i);
        }
        return res;
        

    }
}