统计全1子矩阵个数

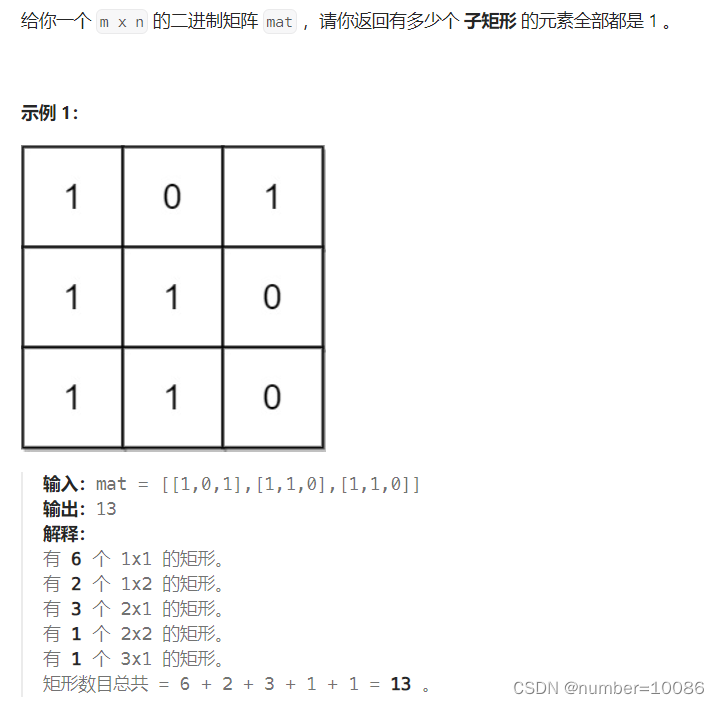
思路1：首先考虑深度优先模拟，从【0，0】出发向下、右扩展，符合条件res++，最后输出res，比较直观，但重复进行了大量节点遍历操作，时间复杂度较高，数据量大时会超时

class Solution {
    unordered_set<int>set;
    int res=0;
    void get(vector<vector<int>>& mat,int start_r,int start_c,int row,int col){
        if(row>=mat.size()||col>=mat[0].size()||
        set.count(start_r+(start_c+((row+col*151)*151))*151)) return;
        for(int i=start_r;i<=row;i++){
            if(!mat[i][col]) return;
        }
        for(int i=start_c;i<=col;i++){
            if(!mat[row][i]) return;
        }
        res++;
        set.insert(start_r+(start_c+((row+col*151)*151))*151);
        get(mat,start_r,start_c,row+1,col);
        get(mat,start_r,start_c,row,col+1);
    }
public:
    int numSubmat(vector<vector<int>>& mat) {
        for(int i=0;i<mat.size();i++){
            for(int j=0;j<mat[0].size();j++){
                get(mat,i,j,i,j);
            }
        }
        return res;
    }
};

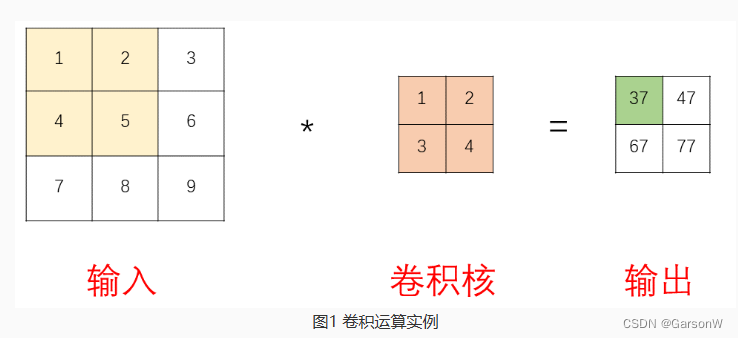
思路2：单考虑行或列时每增加1个1，结果增加 行或列1个数+1，那么多行多列时每增加一行或一列增加（1+2+…+n）*（m+1），加列时：n为行数，m为原来列数，实际上情景就是第一个图的拓展，只不过矩形中的1实际上是长度相等的全1矩形

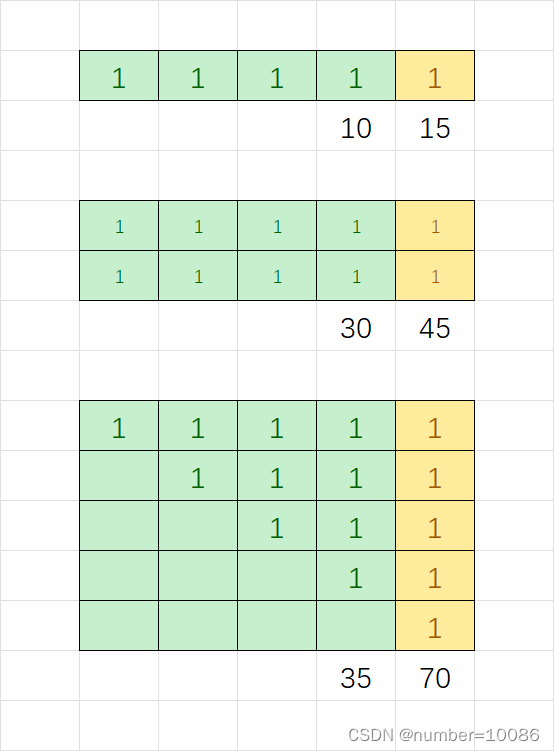
因而仅需要使用一个二维数组tmp存储target[i][j]及前有几个连续的1，然后从上到下加上min(tmp[i][j],tmp_pre_min)即可

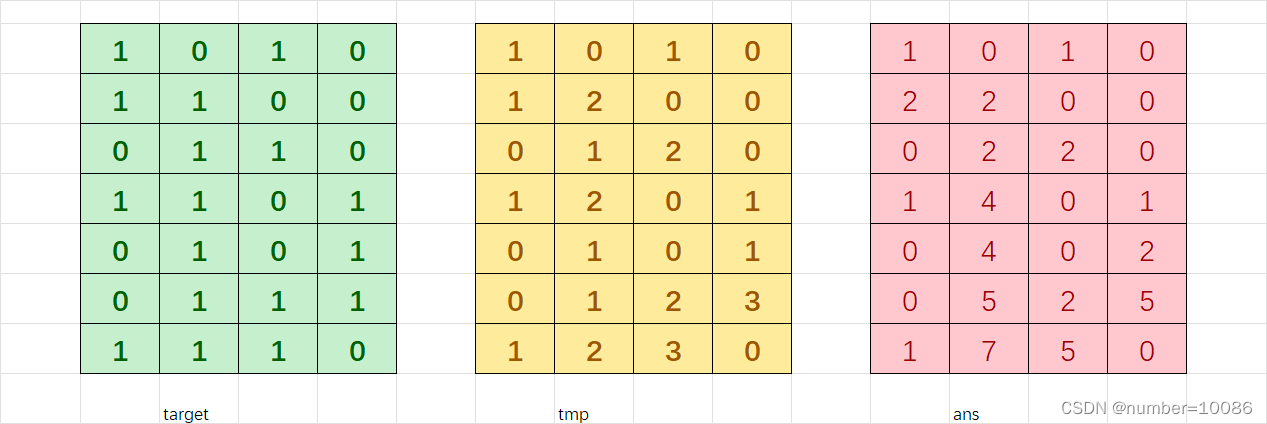
class Solution {
public:
    int numSubmat(vector<vector<int>>& mat) {
        int n = mat.size();
        int m = mat[0].size();
        vector<vector<int> > row(n, vector<int>(m, 0));
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                if (j == 0) {
                    row[i][j] = mat[i][j];
                } else if (mat[i][j]) {
                    row[i][j] = row[i][j - 1] + 1;
                }
                else {
                    row[i][j] = 0;
                }
            }
        }
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                int col = row[i][j];
                for (int k = i; k >= 0 && col; --k) {
                    col = min(col, row[k][j]);
                    ans += col;
                }
            }
        }
        return ans;
    }
};

单调栈优化后代码：

class Solution {
public:
    int numSubmat(vector<vector<int>>& mat) {
        int n = mat.size();
        int m = mat[0].size();
        vector<vector<int> > row(n, vector<int>(m, 0));
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                if (j == 0) {
                    row[i][j] = mat[i][j];
                } else if (mat[i][j]) {
                    row[i][j] = row[i][j - 1] + 1;
                }
                else {
                    row[i][j] = 0;
                }
            }
        }
        int ans = 0;
        for (int j = 0; j < m; ++j) { 
            int i = 0; 
            stack<pair<int, int> > Q; 
            int sum = 0; 
            while (i <= n - 1) { 
                int height = 1; 
                while (!Q.empty() && Q.top().first > row[i][j]) {
                  	// 弹出的时候要减去多于的答案
                    sum -= Q.top().second * (Q.top().first - row[i][j]); 
                    height += Q.top().second; 
                    Q.pop(); 
                } 
                sum += row[i][j]; 
                ans += sum; 
                Q.push({ row[i][j], height }); 
                i++; 
            } 
        } 
        return ans;
    }
};