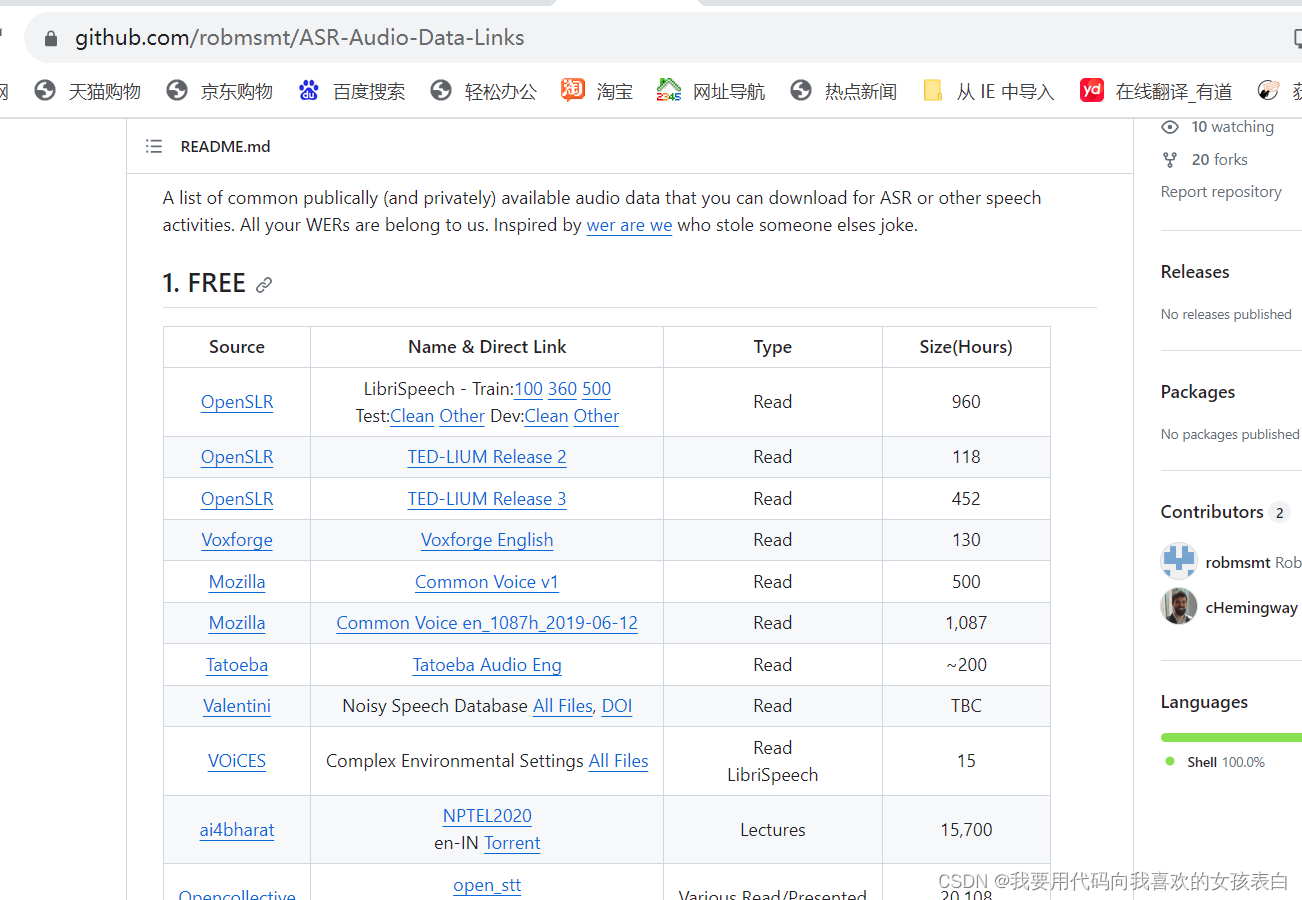
克莱姆法则的几何解释
- 线性方程组求解
- 正交变换
- 克莱姆法则
这是关于3Blue1Brown "线性代数的本质"的学习笔记。
线性方程组求解
克莱姆法则并非解线性方程组的最好方法(高斯消元法更好),了解它是为了加深对线性方程组的理解。

对于
3
x
+
2
y
=
−
4
−
x
+
x
y
=
−
2
\begin{aligned} 3x+2y=-4 \\ -x+xy=-2\end{aligned}
3x+2y=−4−x+xy=−2
可以把这个方程组看作对[x, y]向量的一个已知的矩阵变换

哪个输入向量[x, y]在变换后成为了[-4,-2]?
思路1:
我们已知的向量是矩阵列向量的一个线性组合


行列式不为零意味着线性变换后维数依然相同。即,每个输入向量仅对应一个输出向量,且每个输出向量也仅对应一个输入向量。
正交变换
不改变点积的变换是正交变换。正交变换使基向量在变换后依然保持单位长度,且相互垂直,没有拉伸、压缩、变形。把正交变换可以想象成刚体运动的旋转。
用正交矩阵求解线性系统非常简单,因为点积不变,所以,已知的输出向量和矩阵的列向量的点积,分别等同于未知输入向量和各基向量的点积。也就是输入向量的每一个坐标。


克莱姆法则
有没有另一种对输入向量坐标值的几何解释,能在矩阵变换后保持不变呢?
我们看看行列式。
怎么来求由第一个基向量
i
⃗
\vec{i}
i和未知的输入向量
[
x
,
y
]
T
[x,y]^{T}
[x,y]T组成的平行四边形面积?

面积是长度为1的低,乘上与底边垂直的高,这个高正好是未知向量
[
x
,
y
]
T
[x,y]^{T}
[x,y]T的
y
y
y坐标。

更准确地,应该考虑这个平行四边形的有向面积。如果向量的
y
y
y坐标是负的,则四边形面积也为负。前提是把基向量的
i
⃗
\vec{i}
i放在第一位来定义平行四边形。

举一反三,三维呢?
直观地,在
z
z
z轴上的坐标等于第三个基向量
k
⃗
\vec{k}
k和未知的输入向量
[
x
,
y
]
T
[x,y]^{T}
[x,y]T组成的平行四边形面积,也就是基向量
k
⃗
\vec{k}
k和未知的输入向量
[
x
,
y
]
T
[x,y]^{T}
[x,y]T的叉积。
但有更好的方法。
考虑未知向量与另外两个基向量
i
⃗
\vec{i}
i和
j
⃗
\vec{j}
j所组成的平行六面体


这个平面六面体的底面是由基向量 i ⃗ \vec{i} i和 j ⃗ \vec{j} j组成的正方形,面积是1,所以,它的体积等于它的高,也就是未知向量的z坐标。
同样地,可以用这个奇怪的方法来描述未知向量在某一个轴上的坐标值。

为什么要把坐标和平行四边形或六面体的面积或体积联系在一起?
因为矩阵变换后,平行四边形的面积不一定保持不变,可能成比例增大或减小

但注意:这正是行列式的关键,所有面积伸缩的比例都是一样的!
所有面积收缩的比例就是给定的行列式!


比如考虑一个新的平行四边形,第一条边是变换后的第一基向量(也就是矩阵的第一列),第二条边是变换后的未知向量 [ x , y ] T [x,y]^{T} [x,y]T,那它的面积是多大呢?

其实这就是我们之前提及的平行四边形的变换。变换前,面积是未知输入向量的y坐标值。
所以,变换后的面积等于矩阵的行列式乘以y值(矩阵行列式是面积伸缩比例,y是变换前的面积)。

故,可用输出的平行四边形面积,除以矩阵的行列式计算出y。
y
=
A
r
e
a
d
e
t
(
A
)
y=\frac{Area}{det(A)}
y=det(A)Area
那怎么计算出面积呢?
既然我们已知最终变换后的向量,毕竟这是一个线性方程组,可以构造一个新矩阵,第一列和我们原先的矩阵相同,而第二列是输出向量,然后取新矩阵行列式(其实就是底乘高)。