list.c中主要完成列表数据结构的操作,有列表和列表项的初始化、列表的插入和移除。
2.1列表初始化vListInitialise()
2.1.1函数原型
void vListInitialise( List_t * const pxList )
- pxList:列表指针,指向要初始化的列表。
2.1.2函数框架
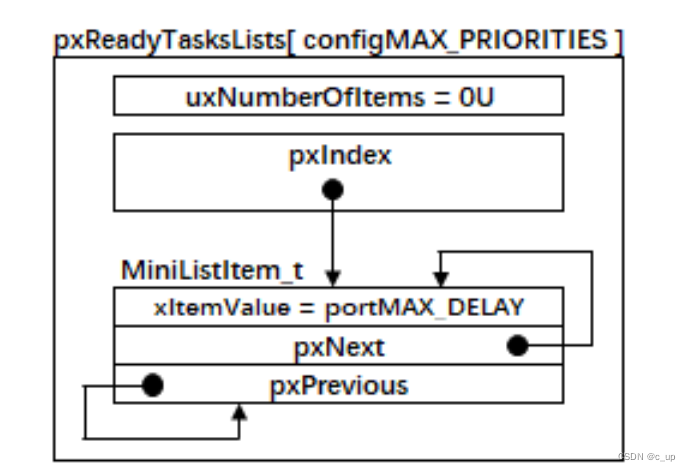
简单来说,列表的初始化就是链表根节点的初始化,如图所示:

2.2列表项初始化vListInitialiseItem()
2.2.1函数原型
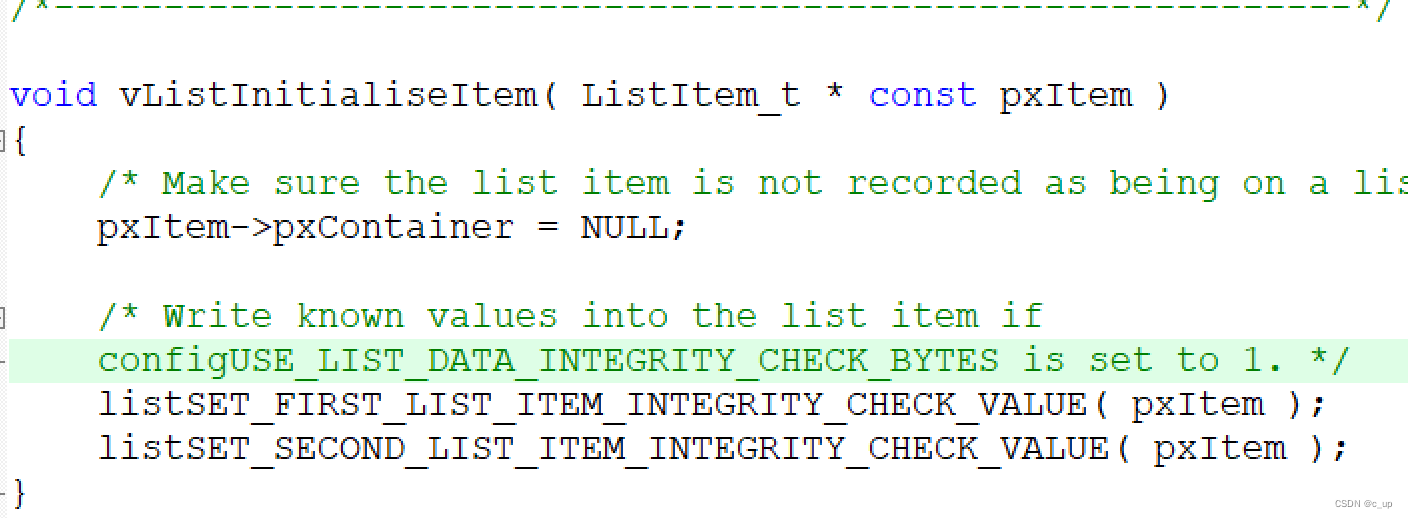
void vListInitialiseItem( ListItem_t * const pxItem )
- pxItem :列表项指针。
2.2.2函数框架
使列表项pxItem->pxContainer=NULL,表示列表项没有所属的列表。
2.3列表项插入列表末尾vListInsertEnd()
2.3.1函数原型
void vListInsertEnd( List_t * const pxList, ListItem_t * const pxNewListItem )
- pxList:列表指针;
- pxNewListItem:要插入的新列表项指针。
2.3.2函数框架


2.4列表项插入列表vListInsert()
2.4.1函数原型
void vListInsert( List_t * const pxList, ListItem_t * const pxNewListItem )
- pxList:列表指针;
- pxNewListItem:要插入的新列表项指针。
2.4.2函数框架
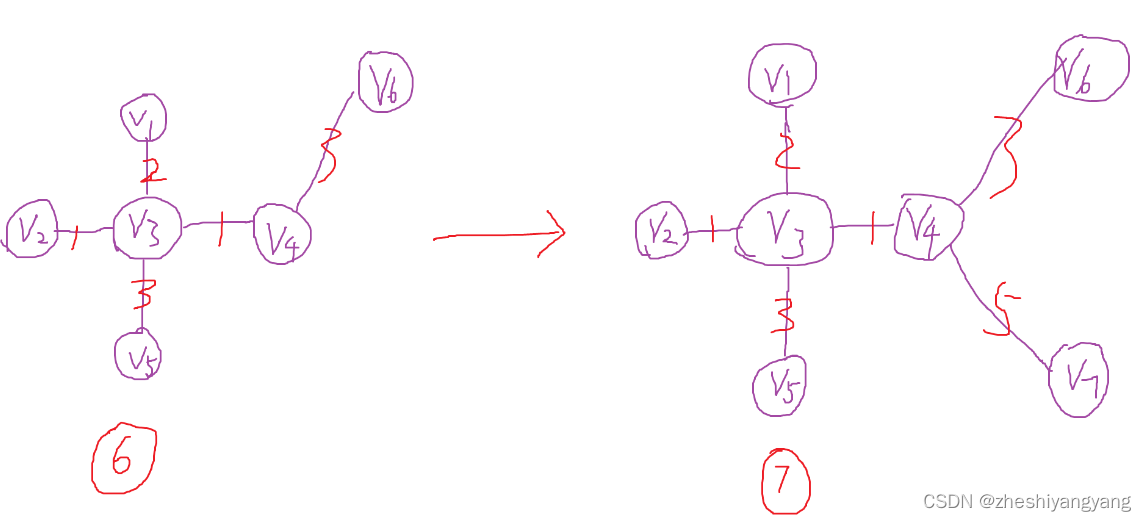
vListInsert()与vListInsertEnd()不同之处在于,可以根据列表项中的value值大小,先和根节点(value值最大)开始比,再由value值小到大找,找到比新列表项value值大的第一个列表项,然后把新列表项插入到它的前面。

2.5列表项移除列表uxListRemove()
2.5.1函数原型
UBaseType_t uxListRemove( ListItem_t * const pxItemToRemove )
- pxItemToRemove:列表项指针,指向要移除的列表项;
- 返回值:被移除列表项所属的列表中列表项的数量。
2.5.2函数框架