引子：

无向图如果是一个网，那么它的所有的生成树中必有一颗生成树的边的权值之和是最小的，我们称

这颗权值和最小的树为：“最小生成树”（MST）。

其中，一棵树的代价就是树中所有权值之和。

而在现实中，最小生成树的概念可以用来解决很多实际问题，例如，在n个城市之间建立交通网，

那么哪一条路径是最短的呢？就可以用最小生成树来解决。

算法思想：

设G = (V,E)为以连通网，其中V为顶点集合，E为带权边集合。

设置两个新集合U和T：

U用于存放最小生成树的顶点，T用于存放最小生成树的边。

令集合的初值为:{u0}(假设构造最小生成树时，从顶点u0出发。)

集合T的初值为{}。

从所有u∈U，v∈V-U的边（u,v）中，选取最小权值的边（u0,v0），将顶点v0加入集合U中，将边

（u0,v0）加入集合T中。

如此不断重复，知道U = V，最小生成树构造完成，集合T中包含了最小生成树中的所有边。

分析算法可知：

为了实现Prim算法，需要一个辅助数组closedge以记录从U到V-U具有最小代价的边。

对于closedge数组需要包含两个域：

adjvex和lowcost，其中lowcost = 0表示若顶点v不在生成树上，用closedge.lowcost存放v与生成树

上的另一个顶点的序号所构成边的权值。

adjvex存放与该边相关联的生成树上的另一顶点的序号。

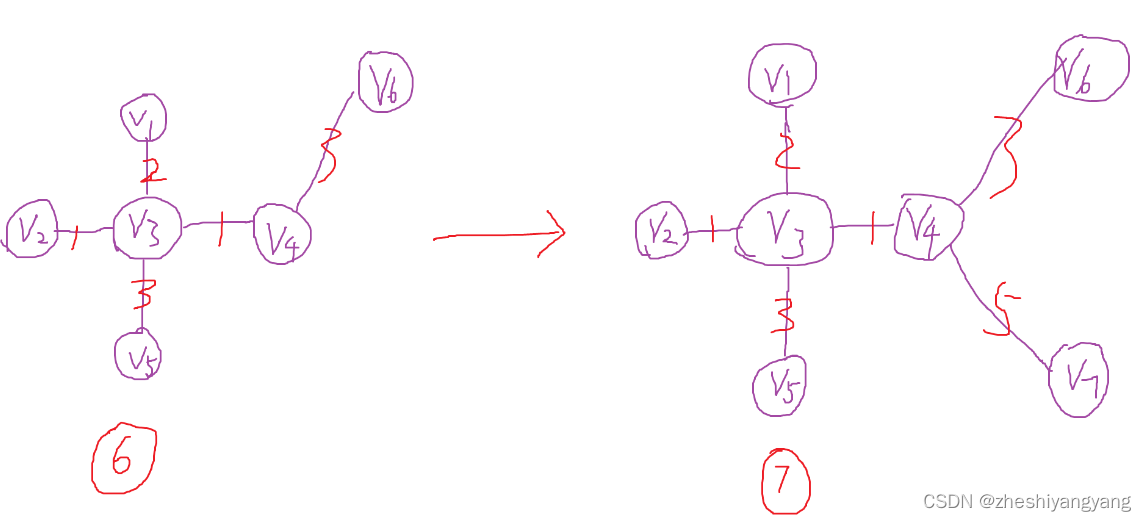
算法生成图

对于下面这个无向图例子来说：

算法的执行过程如下：

代码部分：

#include<stdio.h>
#define MAX 100
typedef struct Mgraph{
	char vertex[MAX];
	int arcs[MAX][MAX];
	int vexnum,arcnum;
}Mgraph;

typedef struct Closedge{
	char adjvex[MAX];
	int lowcost[MAX];
}Closedge;

int LocateVerTex(Mgraph *G,char v)
{
	int k;
	for(k=0;k<G->vexnum;k++)
		if(G->vertex[k] == v)
			return k;
	return -1;
}

void CreateMgraph(Mgraph *G)
{
	int i,j,weight,adj1,adj2;
	char v1,v2;
	printf("请输入顶点数和边数:\n");
	scanf("%d %d",&G->vexnum,&G->arcnum);
	getchar();
	printf("请输入:{%d}个顶点:\n",G->vexnum);
	for(i=0;i<G->vexnum;i++)
		scanf("%c",&G->vertex[i]);
	getchar();
	printf("请输入:{%d}条边:(格式如下:v1 v2 权值).\n",G->arcnum);
	for(i=0;i<G->vexnum;i++){
		for(j=0;j<G->vexnum;j++){
			G->arcs[i][j] = 0;
		}
	}
	for(i=0;i<G->arcnum;i++){
		scanf("%c %c %d",&v1,&v2,&weight);
		getchar();
		adj1 = LocateVerTex(G,v1);
		adj2 = LocateVerTex(G,v2);
		if(adj1 == -1 || adj2 == -1){
			printf("失败.\n");
			i = i - 1;
			continue;
		}
		else{
			G->arcs[adj1][adj2] = weight;
			G->arcs[adj2][adj1] = weight;
			printf("成功.\n");
		}
	}
}

int MiniNum(Closedge *closedge,Mgraph *G)
{
	int j,p = 1,min = 999;
	for(j=0;j<G->vexnum;j++){
		if(closedge->lowcost[j] != 0 && closedge->lowcost[j] < min){
			min = closedge->lowcost[j];
			p = j;
		}
	}
	return p;
}

void MiniTree_Prim(Mgraph *G,char u)
{
	int i,j,k,num;
	k = LocateVerTex(G,u);
	Closedge closedge;
	for(i=0;i<G->vexnum;i++){
		if(i!=k){
			closedge.adjvex[i] = u;
			closedge.lowcost[i] = G->arcs[k][i];
		}
	}
	closedge.lowcost[k] = 0;
	printf("最小生成树的各条边为:\n");
	for(i=1;i<G->vexnum;i++){
		k = MiniNum(&closedge,G);
		printf("边:<%c,%c>,权值为{%d}:\n",closedge.adjvex[k],G->vertex[k],closedge.lowcost[k]);
		closedge.lowcost[k] = 0;
		for(j=0;j<G->vexnum;j++){
			if(G->arcs[k][j] < closedge.lowcost[j]){
				closedge.adjvex[j] = G->vertex[k];
				closedge.lowcost[j] = G->arcs[k][j];
			}
		}
	}
}

int main()
{
	Mgraph G;
	CreateMgraph(&G);
	MiniTree_Prim(&G,'A');
	return 0;
}