目录
一、概念题
二、计算题
1、节点数
2、深度
3、遍历序列
一、概念题
1、在用树表示的目录结构中,从根目录到任何数据文件,有( )通道
答案:唯一一条,树的特点是不相交,所以不可能有多个路径同时到达一个点。
2、下列关于树的叙述正确的是( )
A.树中可以有环
B.树的度是指所有结点中度最小的结点的度
C.树的深度指的是结点数最多的那一层的深度
D.树的根结点是所有结点的祖先结点
答案:D
A: 树中的节点不能相交
B: 树的度为所有节点中度最大的节点的度
C: 树的深度为根节点到叶子节点的最大深度
3、下列关于二叉树的叙述错误的是( )
A.二叉树指的是深度为 2 的树
B.一个 n 个结点的二叉树将拥有 n-1 条边
C.一颗深度为 h 的满二叉树拥有 2^h-1 个结点(根结点深度为1)
D.二叉树有二叉链和三叉链两种表示方式
答案:A
A错误: 二叉树指最大孩子个数为2,即树的度为二的树。深度描述的为树的层数。
B正确: 对于任意的树都满足:边的条数比节点个数少1,因为每个节点都有双亲,但是根节点没有
C正确: 正确,参加二叉树性质
D正确: 二叉链一般指孩子表示法,三叉连指孩子双亲表示法,这两种方式是二叉树最常见的表示方式,虽然还有孩子兄弟表示法,该中表示方式本质也是二叉链
4、在一颗完全二叉树中,某一个结点没有其左孩子,则该结点一定( )
A.是根结点
B.是叶结点
C.是分支结点
D.在倒数第二层
答案:B
完全二叉树中如果一个节点没有左孩子,则一定没有右孩子,必定为一个叶子节点,最后一层一定为叶子节点,但是倒数第二层也可能存在叶子节点。
5、一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反,则该二叉树一定满足 ()
A.所有的结点均无左孩子
B.所有的结点均无右孩子
C.只有一个叶子结点
D.至多只有一个结点
答案:C
- 前序遍历:根 左 右
- 后序遍历:左 右 根
从二叉树 前序 和 后序遍历结果规则中可以看出,如果树中每个节点只有一个孩子时,遍历结果肯定是反的
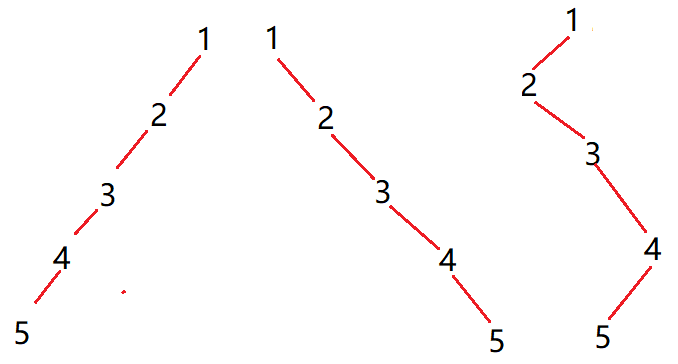
比如下面这前序和中序序列所构成的树的结构:
- 12345
- 54321
故每个节点只有一个孩子,即只有一个叶子节点
二、计算题
1、节点数
1、在一颗度为3的树中,度为3的结点有2个,度为2的结点有1个,度为1的结点有2个,则叶子结点有( )个
答案为 6 个。
- 设度为i的节点个数为ni, 该树总共有n个节点,则n=n0+n1+n2+n3.
- 有n个节点的树的总边数为n-1条.
- 根据度的定义,总边数与度之间的关系为:n-1=0*n0+1*n1+2*n2+3*n3.
- 联立两个方程求解,可以得到n0 = n2 + 2n3 + 1, n0=6
2、一颗完全二叉树有1001个结点,其叶子结点的个数是( )
答案:501
- 在任意二叉树中,度为0的节点都比度为2的节点多1个,即 n0 = n2 + 1
- 另外,在完全二叉树中,如果节点总个数为奇数,则没有度为1的节点,如果节点总个数为偶数,只有一个度为1的节点
- 因此:n0 + n1 + n2 = 1001 节点总数为奇数,没有度为1的节点
- n0 + 0 + n2 = 2*n0-1 = 1001 n0 = 501
3、设一棵二叉树中有3个叶子结点,有8个度为1的结点,则该二叉树中总的结点数为( )个
答案:13
- 设Ni表示度为i的节点个数,则节点总数 N = N0 + N1 + N2
- 节点个数于节点边的关系: N个节点的树有N-1个边
- 边与度的关系:N - 1 = N1 + 2 * N2
- 故:N0 + N1 + N2 - 1 = N1 + 2 * N2
- 因此,得:N0 = N2 + 1
- 回到原题,N0 = 3,N1 = 8,可得N2 = 2。
- 因此答案是 3 + 8 + 2 = 13。
4、2-3树是一种特殊的树,它满足两个条件:
(1) 每个内部结点有两个或三个子结点
(2) 所有的叶结点到根的距离相同
如果一颗2-3树有10个结点,那么它有( )个叶结点。
答案:6
根据题目意思,每一个非叶子节点至少有两个孩子节点,并且叶子节点都在同一层,所以,假设树的高度为h, 则二三树种最小的节点个数为满二叉树的个数:2^h - 1, 最大个数: (3^h - 1) / 2。所以 2^h - 1 < 10 < (3^h - 1) / 2, h为3,结构是1(3(2,2,2))。所以叶节点个数为6
5、设某种二叉树有如下特点:每个结点要么是叶子结点,要么有2棵子树。假如一棵这样的二叉树中有m(m>0)个叶子结点,那么该二叉树上的结点总数为( )
答案:2m-1
- 根据二叉树的性质,在任意的二叉树中,度为0的节点比度为2的节点多1个
- 现在叶子节点为m个,即度为0的节点有m个,那度为2的节点个数就为m-1个
- 而题目说该二叉树中只有度为2和度为0的节点 ,
- 因此总的节点数就为:m+m-1 = 2m-1
6、对任意一颗二叉树,设N0、N1、N2分别是度为0、1、2的结点数,则下列式子中一定正确的是( )
A.N0 = N2 + 1
B.N1 = N0 + 1
C.N2 = N0 + 1
D.N2 = N1 + 1
答案:A
节点总数N: N = N0 + N1 + N2
度和边的关系: N - 1 = 0 * N0 + 1 * N1 + 2 * N2
上面两个式子可以推出: N0 + N1 + N2 - 1 = N1 + 2 * N2
可得: N0 = N2 + 1
2、深度
1、一颗拥有1000个结点的树度为4,则它的最小深度是( )
答案:6
如果这棵树每一层都是满的,则它的深度最小,假设它为一个四叉树,高度为h,则这个数的节点个数为(4^h - 1) / 3,当h = 5, 最大节点数为341, 当h = 6, 最大节点数为1365,所以最小深度应该为6。
3、遍历序列
1、 已知某二叉树的前序遍历序列为5 7 4 9 6 2 1,中序遍历序列为4 7 5 6 9 1 2,则其后序遍历序列为( )
答案:4 7 6 1 2 9 5
通过前序遍历找到子树的根,在中序遍历中找到根的位置,然后确定根左右子树的区间,即根的左侧为左子树中所有节点,根的右侧为右子树中所有节点。
- 故:根为: 5
- 5的左子树:4 7 5的右子树: 6 9 1 2
- 5的左子树的根为: 7 5的右子树的根为:9
- 7的左子树: 4 7的右:空 9的左子树:6 9的右子树:2
故这棵树的结构如下,即后序遍历: 4 7 6 1 2 9 5
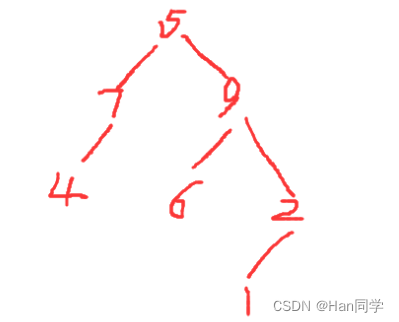
2、.已知某二叉树的中序遍历序列为JGDHKBAELIMCF,后序遍历序列为JGKHDBLMIEFCA,则其前序遍历序列为( )
答案:A B D G J H K C E I L M F
由后序遍历确定子树的根,后序遍历从后向前看,最后一个元素为根,和前序遍历刚好相反,从后向前看后序遍历,应该是根,右,左,根据中序遍历确定子树的左右区间
故:根为: A
- A的左子树:JGDHKB A的右子树:ELIMCF
- A的左子树的根:B A的右子树的根:C
- B的左子树:JGDHK B的右子树:空 C的左子树:ELIM C的右子树:F
- B的左子树的根:D C的左子树根:E
- D的左子树的根:G D的右子树的根:H E的右子树的根:I
故树的结构如下,前序遍历:A B D G J H K C E I L M F
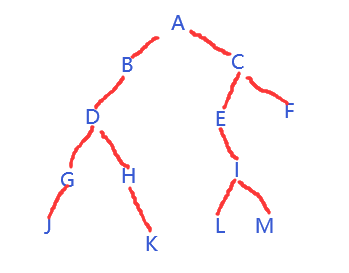
3、.已知某二叉树的前序遍历序列为ABDEC,中序遍历序列为BDEAC,则该二叉树( )
A.是满二叉树
B.是完全二叉树,不是满二叉树
C.不是完全二叉树
D.是所有的结点都没有右子树的二叉树
答案:C
前序确定根,中序找到根确定根的左右子树,最后还原二叉树为:
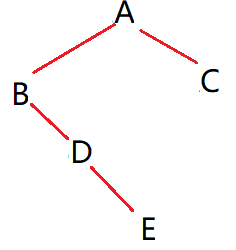
前: ABDEC 中:BDEAC
所以既不是满二叉树,也不是完全二叉树
4、二叉树的后序非递归遍历中,需要的额外空间包括( )
A.一个栈
B.一个队列
C.一个栈和一个记录标记的顺序表
D.一个队列和一个记录标记的顺序表
答案:C
需要一个栈模拟递归的过程, 一个顺序表保存节点。
5、二叉树的( )遍历相当于广度优先遍历,( )遍历相当于深度优先遍历
答案:层序 前序
- 广度优先需要把下一步所有可能的位置全部遍历完,才会进行更深层次的遍历,层序遍历就是一种广度优先遍历。
- 深度优先是先遍历完一条完整的路径(从根到叶子的完整路径),才会向上层折返,再去遍历下一个路径,前序遍历就是一种深度优先遍历。
6、如果一颗二叉树的前序遍历的结果是ABCD,则满足条件的不同的二叉树有( )种
答案:14
首先这棵二叉树的高度一定在3~4层之间:
三层:
- A(B(C,D),()), A((),B(C,D)), A(B(C,()),D), A(B((),C),D),
- A(B,C(D,())), A(B,C((),D))
四层:
- 如果为四层,就是单边树,每一层只有一个节点,除过根节点,其他节点都有两种选择,在上层节点的左边还是右边,所以2*2*2共8种
总共为14种。
![洛谷P1024 [NOIP2001 提高组] 一元三次方程求解(优雅的暴力+二分,干净利落)](https://img-blog.csdnimg.cn/ac019003e7714b9ebf996a71d60c68b0.jpeg)