语法分析基本概念

前置知识
词法层面：采用正规式和有限自动机描述和识别语言的单词符号
语法层面：用上下文无关文法描述语法规则

上下文无关文法(CFG)
四元式G=($V_T$,$V_N$,$S$,$P$)
$V_T$: 终结符集合，非空
$V_N$: 非终结符集合，非空，表示各层次的句法单位
S: 文法的开始符号，S$\in V_N$ 指程序这个句法单位
P: 产生式集合，产生式形为$P->\alpha$ , $P\in V_N$ , $\alpha \in (V_N\cup V_T{)}^{\ast }$

直接推出和推导
直接推出：根据产生式得到，举个例子，当$A->\gamma \in P$且$\alpha 、\beta \in (V_T\cup V_N{)}^{\ast }$ 是，则有$\alpha A\beta ->\alpha \gamma \beta$ ，即$\alpha A\beta$直接推出$\alpha \gamma \beta$
推导：经过多步直接推出得到，若${\alpha }_1->{\alpha }_2->...->{\alpha }_n$，则${\alpha }_1$可以推导出${\alpha }_n$

句子、句型、语言的概念
句型：S推导得到的串

句子：仅含终结符的句型
语言：文法G产生的所有句子的集合，记为$L(G)$

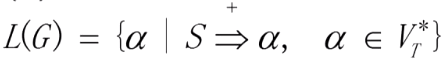
语法分析的任务
分析一个文法的句子的结构，用语法分析树表示

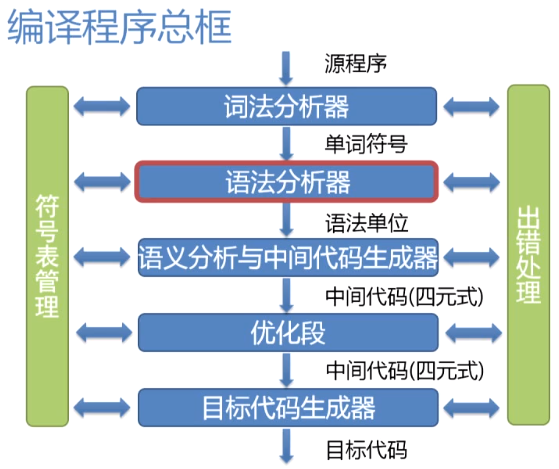
语法分析器的功能
按照文法产生式P，识别输入串(词法分析结果)是否为一个句子(一个形式上正确的程序)

语法分析的地位
在编译器中起主导、推动作用

语法分析分类

自上而下语法分析

基本思想
从文法的开始符号开始，向下推导，推出句子/从语法分析树的根开始，自上而下逐步构建出整个树
分析示例

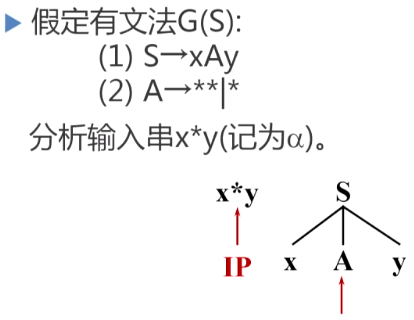
说明：IP可以视为调用词法分析器，调用一次就得到输入单词

自上而下语法分析的问题

回溯问题
候选式重新选择

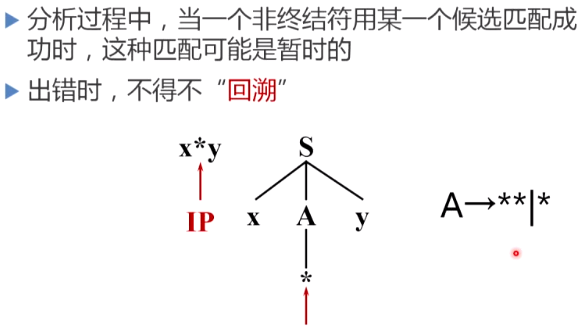
如何避免回溯问题的出现，即是说当自上而下进行推导的过程中出现某一非终结符有多个候选式的情况，如何选择正确的候选式进行语法分析？

文法左递归
出现输入串的语法分析停止向前推进但语法分析树不断增长的情况

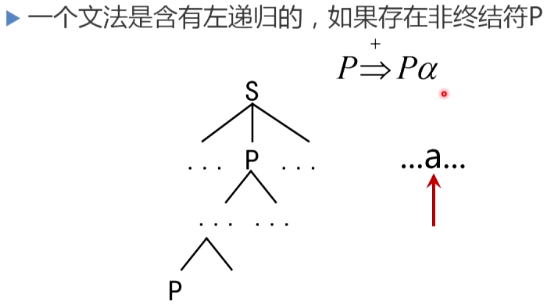
消除文法左递归

文法左递归分为直接左递归和间接左递归两种，下面将分别叙述这两种左递归的消除方法

消除直接左递归

左递归变为右递归，需要满足的条件在于产生式转换后得到的短语不会变化

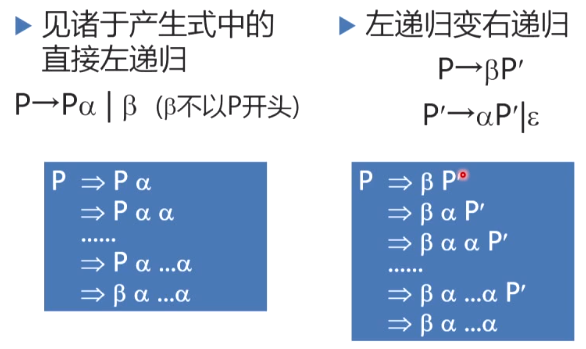
一个适用更普遍的消除直接左递归的示例

习题（ps: 产生式不要忘记$ϵ$ ）

消除间接左递归

一个间接左递归的例子

方法的适用条件

如何改造
将间接左递归通过推导转化为某非终结符的直接左递归，再通过左递归转右递归的方式消除得到的直接左递归

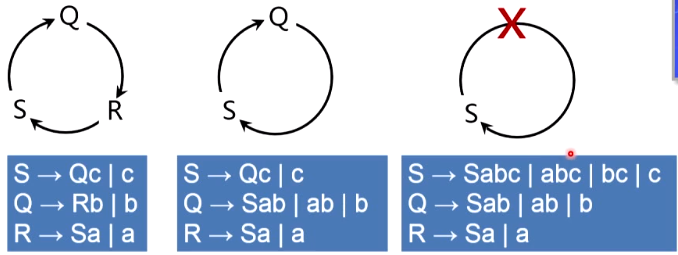
消除左递归的算法

习题

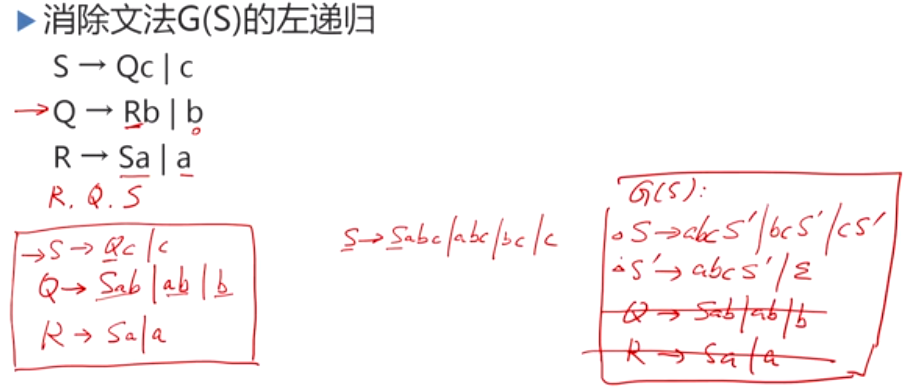
需要注意的问题：

1. 算法中最后一步是消除从S（开始符号）永远无法到达的非终结符的产生式。在习题中即是说Q、R是S推导无限多步也不会得到的，因而是无用的，这两个非终结符的作用已经被$S^{\prime }$发挥了
2. 消除左递归算法中对非终结符的排序是feel free的，不同的排序方式会得到不同的文法形式，但他们所定义的语言是相同的

解决回溯问题

消除回溯的前提

FIRST集与提出公共左因子

怎么选择合适的候选式，根据当前输入字符，选择以当前输入字符开头的候选式，或是以能够推出当前输入字符的非终结符开头的候选式

FIRST集

终结首符集，G中每个非终结符的每个候选式都有一个FIRST集$FIRST(\alpha )$

消除回溯的必要条件之一

提取左公共因子

使得一个非终结符的多个候选式的首字符集尽可能不相交
引入新的非终结符，使得左公共因子只出现一次

FOLLOW集合

考虑$ϵ$ 候选的情况
文法定义如下

分析结果

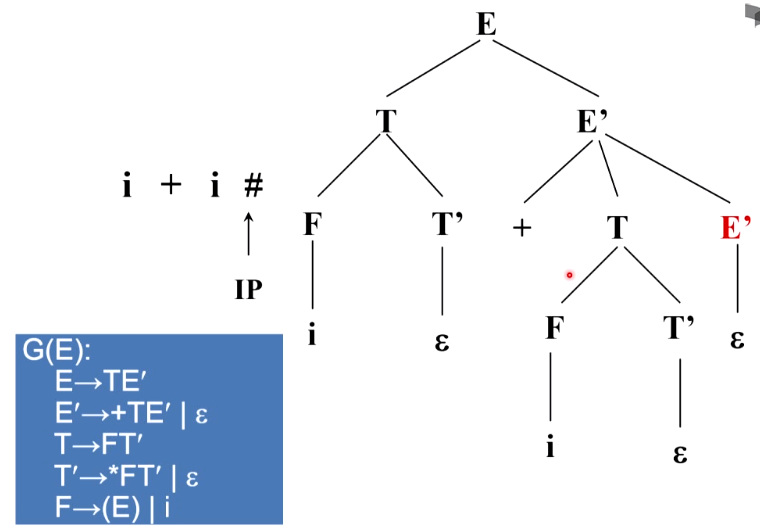
考虑这样一个格局，这这个格局里面出现句型$i{T}^{\prime }+$，即是说+会跟在T’后面，于是在匹配输入时，我们将T’推为了$ϵ$

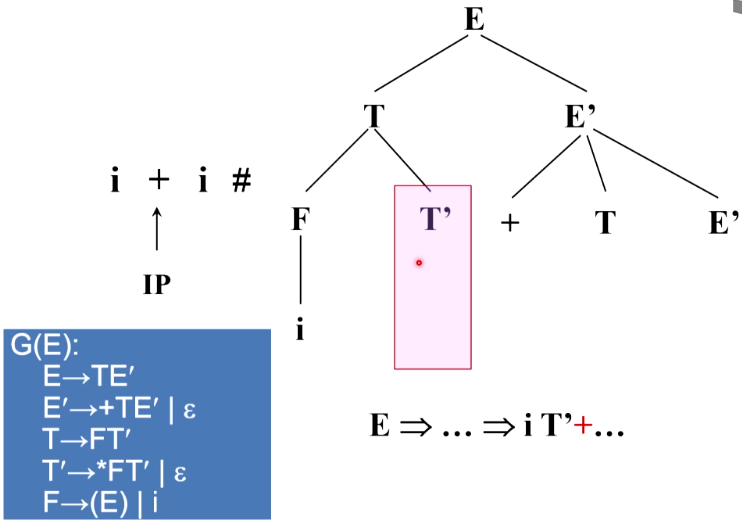
FOLLOW集合
用来说明一个非终结符号后面能跟什么终结符
定义

怎么用

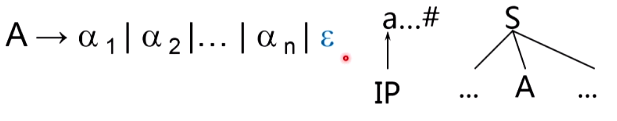
当当前输入符号不在A的任何候选首符集中时，若a出现在了A的FOLLOW集中，并且A有$ϵ$候选，则这里可将A推导为$ϵ$
注意

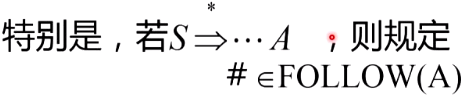
构造FIRST集和FOLLOW集

将对无穷推导空间的考察转变为对有限产生式的反复扫描得到结果

构造FIRST集合

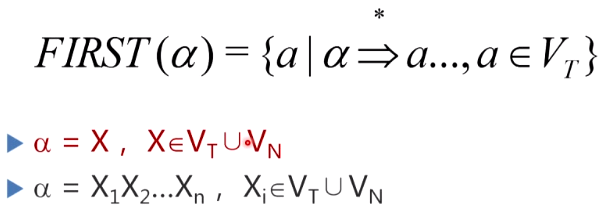
构造每个文法符号的FIRST集合

注意：

1. 有$X->Y...$且$ϵ\in FIRST(Y)$并不能说明$ϵ$属于FIRST(Y)，因为我们不知道…里面是否包含了其他非$ϵ$的终结符
2. 注意终止扫描的条件

构造任何符号串的FIRST集合

构造FOLLOW集合

在每个句型中，能够跟在该非终结符后面的终结符

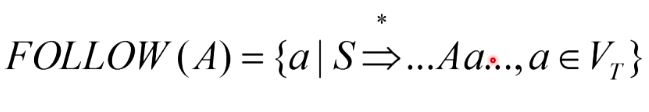
构造方法
扫描产生式右部，寻找非终结符

注意：

1. 终止条件为不再有任何非终结符的FOLLOW集发生变化
2. $A->\alpha B\beta$ 中B为一非终结符，$\alpha$和$\beta$为终结符或非终结符

LL(1)文法

文法条件

LL(1)文法：
第一个L指从左到右扫描输入串
第二个L指最左推导
1指每一步都是根据当前的单词来找候选式，即每一步只需向前查看一个符号
判断方式

1. 消除文法的左递归
2. 提取左公共因子
3. 验证处理后的文法是否满足这三个条件

LL(1)分析法

分析过程

1. 消除左递归
2. 提取左公共因子
3. 计算FIRST集和FOLLOW集
4. 判断该文法是否为LL(1)文法，若满足，则对其进行自上而下的分析

一个示例

下图中展示的为一消除了左递归的文法G


技巧：FIRST集计算看产生式的左部

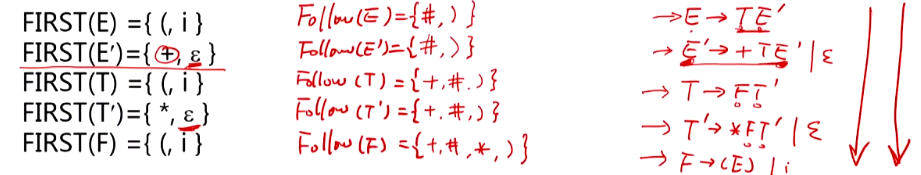
FOLLOW集求解技巧：看产生式右部，一个非终结符的右部符号的first集？最右部的非终结符需要考虑产生式左部的follow集，一个非终结符的右部符号是否能推为$ϵ$

参考资料

1. 国防科技大学编译原理课程视频