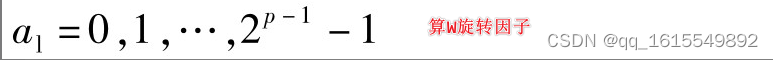DFT到FFT

这是DFT公式

在这里插入图片描述

对DFT代数变换

将DFT的计算，分为计数组和偶数组。
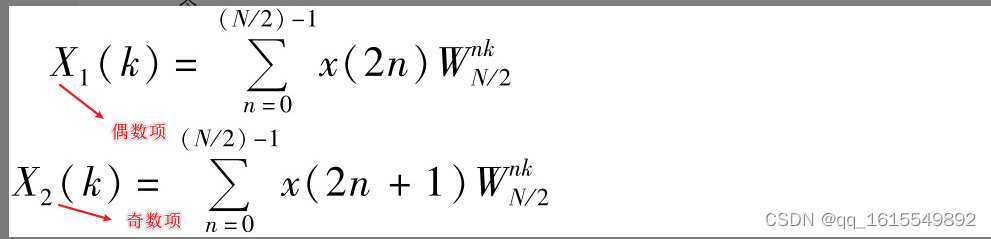
在这里插入图片描述
惊奇的发现：只需要改变 $W_k^N$ 的符号即可得到X（k）的另一半项数的结果。

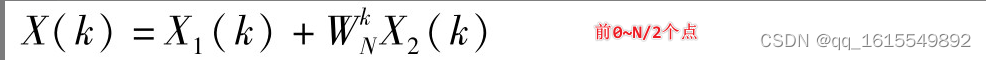
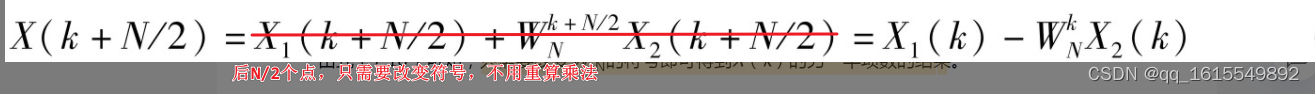
得到FFT算法（蝶形运算）

惊奇的发现：只需要改变 $W_k^N$ 的符号即可得到X（k）的另一半项数的结果。–非常重要的结论
画出蝶形图：
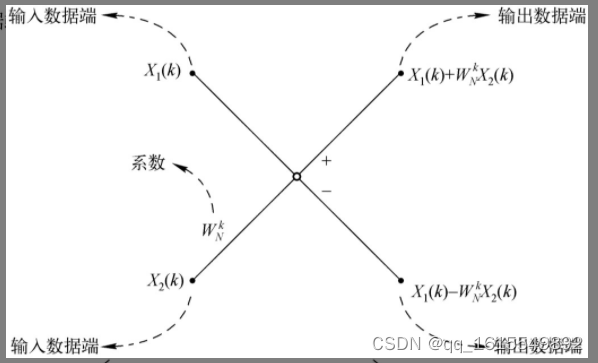
在这里插入图片描述

FFT拆解结论

总是将x（n）分解为一个偶序列和一个奇序列，之后再分别对偶序列和奇序列进行奇偶分解，以此方式重复操作。这种将原始序列x（n）不断分解为奇、偶子序列来进行蝶形运算的算法称为按时间抽取（Deci-mation In Time，DIT）的FFT算法。对于长度为8的序列x（n），先将其分解为两个长度为4的子序列，再将每个子序列分解为两个长度为2的子序列。

蝶形运算特征

蝶形运算的数据包括3类：输入数据、输出数据和旋转因子。在FPGA中，对数据的管理体现为对相应的存储单元的管理，而对存储单元的管理最终是对读、写地址等控制信号的管理。
对于N（ $N=2^M$ ，M为正整数）点基2 FFT算法，共需要进行M级循环计算，每级计算中包含 $2^{M-1}$ 个基2蝶形运算。
同一级中，每个蝶形运算是独立的，这种独立性体现在两个方面：一方面，每个蝶形运算的两个输入数据只对本次蝶形运算有效，不受其他蝶形运算干扰，且输入、输出节点在同一条水平线上，这样，除了第1级运算时需要对输入数据进行基2倒序外，其他计算都可以采取原位（In-Place）操作方式进行；另一方面，蝶形运算的顺序没有先后之分（因为是原位运算，每个乱序算完后就知道存在何处地址）。
采用D.Cohen方法来存储。