大家好，我是带我去滑雪！

      密度聚类（Density-based Clustering）和层次聚类（Hierarchical Clustering）是两种不同的聚类方法，用于将数据集中的数据点分组成簇。

目录

一、密度聚类

（1）DBSCAN

（2）DBSCAN计算方式

（3）DBSCAN算法的优缺点

（4）代码实现

二、层次聚类

（1）什么是层次聚类

（2）层次聚类的优缺点

（3）代码实现

---

一、密度聚类

（1）DBSCAN

       DBSCAN(Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法)是一种很典型的密度聚类算法，该算法将具有足够密度的区域划分为簇，并在具有噪声的空间库中发现任意形状的簇，它将簇定义为密度相连的点的最大集合。DBSCAN既可以适用于凸样本集，也可以适用于非凸样本集。

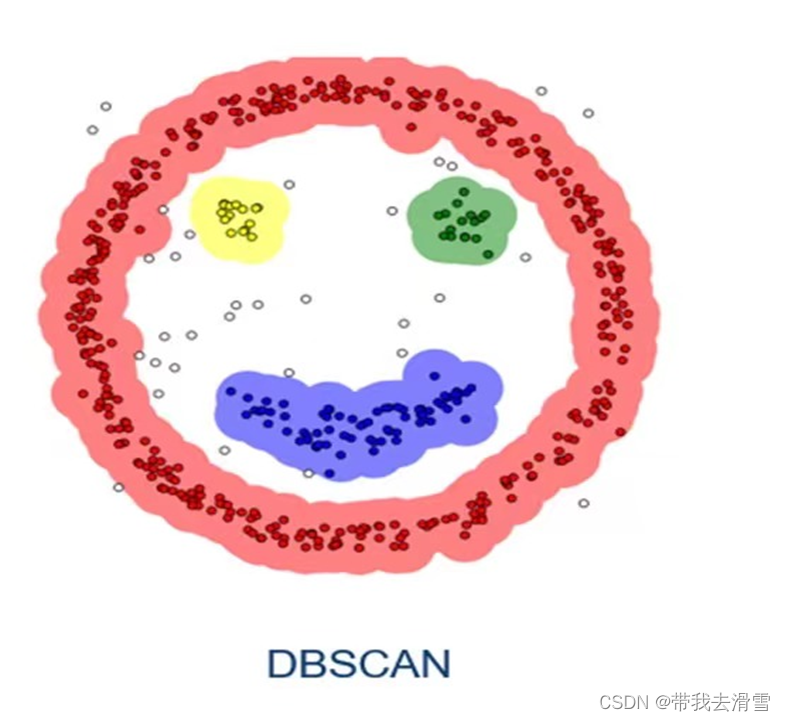
        DBSCAN的核心思想是基于密度的。从直观效果上看，DBSCAN算法可以找到样本点的全部密集区域，并把这些密集区域当做一个一个的聚类簇。

        DBSCAN含有两个超参数：邻域半径Eps和最少点数目MinPts。这两个算法参数实际可以刻画什么叫密集——当邻域半径Eps内的点的个数大于最少点数目MinPts时，就是密集。

邻域（Eps）：以给定对象为圆心，半径内的区域为该对象的邻域；核心对象：对象的邻域内至少有MinPts（设定的阈值）个对象，则该对象为核心对象；边界点：对象的领域小于MinPts个对象，但是在某个核心对象的邻近域中；离群点（噪声）：对象的领域小于MinPts个对象，且不在某个核心对象的邻域中。

（2）DBSCAN计算方式

       1)密度直达：给定一个对象集合D，如果P为核心点，Q在P的Eps邻域内，那么称P到Q密度直达(Directly Density-Reachable)。任何核心点到其自身密度直达，密度直达不具有对称性，如果P到Q密度直达，那么Q到P不一定密度直达。

      2)密度可达：如果存在核心点P2，P3，……，Pn，且P1到P2密度直达，P2到P3密度直达，……，P(n-1)到Pn密度直达，Pn到Q密度直达，则P1到Q密度可达(Density-Reachable)。密度可达也不具有对称性。

     3)密度相连：如果存在核心点S，使得S到P和Q都密度可达，则P和Q密度相连(Density-Connected)。密度相连具有对称性，如果P和Q密度相连，那么Q和P也一定密度相连。密度相连的两个点属于同一个聚类簇。

（3）DBSCAN算法的优缺点

DBSCAN算法的优点：

• （1）不需要预先确定聚类的数量。
• （2）可以很好地发现任意尺寸和任意形状的聚类。
• （3）可以在聚类的同时发现异常点，对数据集中的异常点不敏感。
• （4）聚类结果没有偏倚，而k-means之类的聚类算法的初始值对聚类结果有很大影响。

DBSCAN算法的缺点：

• （1）如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。
• （2）如果样本集较大时，聚类收敛时间较长，尤其在我们定义的距离计算方式较为复杂的时候。
• （3）调参比较复杂，eps、MinPts的设置不同对结果会产生较大影响，需要多次尝试以获取最佳的聚类效果

（4）代码实现

from sklearn.cluster import DBSCAN

import numpy as np

# 输入数据

X = np.array([(1,1), (1,2), (2,1), (8,8), (8,9), (9,8), (15,15)])

# 创建DBSCAN对象，设置半径和最小样本数

dbscan = DBSCAN(eps=2, min_samples=3)

# 进行聚类

labels = dbscan.fit_predict(X)

# 输出聚类结果

for i in range(max(labels)+1):

    print(f"Cluster {i+1}: {list(X[labels==i])}")

print(f"Noise: {list(X[labels==-1])}")

二、层次聚类

（1）什么是层次聚类

        层次聚类试图在不同层次对数据集进行划分，从而形成树形的聚类结构。数据集的划分可采用“自底向上”的聚合策略，也可采用“自顶向下”的分拆策略。

凝聚的层次聚类：AGENS算法

       是一种自底向上聚合策略的层次聚类算法。它先将数据集中的每一个样本看作一个初始聚类，然后按照一定规则，例如类间距离最小，将最满足规则条件的两个类进行合并。如此反复进行，每次减少一个类，直到满足停止条件。需要预先确定下面三个要素:

• 距离或相似度：欧氏距离、曼哈顿距离、夹角余弦等
• 合并规则：最短距离，最长距离，中心距离，平均距离等
• 停止条件：类的个数达到阈值、类的直径超过阈值等

（2）层次聚类的优缺点

优点：

• 多层次的聚类结构：层次聚类生成一个树状结构，可视化呈现数据点的多个层次聚类结果，使得用户可以在不同的抽象层次上研究数据的结构。这有助于更全面地理解数据。
• 不需要事先指定簇的数量：与许多其他聚类算法不同，层次聚类不需要事先确定簇的数量，因为它可以根据数据的结构自动形成不同层次的聚类。
• 可视化和解释性强：通过绘制层次聚类的树状图，可以直观地表示数据点如何组织成不同的簇。这种可视化有助于解释和理解数据的结构。
• 适用于小规模数据集：层次聚类适合处理相对较小规模的数据集，因为它的时间和空间复杂度可能随着数据规模的增加而增加。

缺点：

• 计算复杂性高：层次聚类的计算复杂性通常比其他聚类算法高，特别是对于大规模数据集而言。构建层次结构可能需要大量的计算资源。
• 不适用于大规模数据：由于计算复杂性高，层次聚类通常不适用于大规模数据集，因为它可能需要很长的时间来完成聚类分析。
• 不适用于凸簇：层次聚类在处理凸形状的簇时可能效果不如一些其他算法，因为它更适合于发现非凸形状的簇。
• 难以处理噪声：层次聚类通常难以处理噪声数据点，因为噪声可能会导致树状结构中的多个分支，使得解释和选择合适的聚类层次更加困难。

（3）代码实现

import math

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt 

from scipy.cluster.hierarchy import linkage,dendrogram

# 从excel中读取数据

def load_data(path):

       # 从excel中读取数据，并用dataframe存储

       global df

       df = pd.read_excel(path)

       # 将dataframe中的数据值转换为列表

       df_li = df.values.tolist()

       # 将存储好数据的列表转换为数组

       dataSet = []

       for i in df_li:

              tmp = []

              tmp.append(i)

              dataSet.append(tmp)

       # 返回

       return dataSet

# 计算欧式距离

def distance(pointA,pointB):

       dis = 0

       for i in range(len(pointA)):

              dis += (pointA[i]-pointB[i])**2

       return math.sqrt(dis)

# 寻找最小距离

def Matrix_min(pointsA,pointsB,indexA,indexB,result):

       for pointA in pointsA:

              tmp_min_dis = 10000

              for pointB in pointsB:

                     dis = distance(pointA,pointB)

              if dis < tmp_min_dis:

                     tmp_min_dis = dis

       result.append({'indexA':indexA,'indexB':indexB,'dist':tmp_min_dis})

# 利用最小簇间距离度量聚类

def search_mindis(result):

       tmp_min_dis = 10000

       tmp_min_list = []

       for i in result:

              if i['dist'] < tmp_min_dis:

                     tmp_min_dis = i['dist']

                     tmp_min_list = []

                     tmp_min_list.extend([i['indexA'],i['indexB']])

              elif i['dist'] == tmp_min_dis:

                     tmp_min_list.extend([i['indexA'],i['indexB']])

       return list(set(tmp_min_list))

# 层次聚类，合并样本，并原数据集中删除元素

def mergeGroup(array, mergeIndexs):

    mergeIndexs.sort()

    rangeLen = len(mergeIndexs) - 1;

    for i in range(rangeLen):

        array[mergeIndexs[0]].extend(array[mergeIndexs[i+1]])

    mergeIndexs.reverse()

    for i in range(rangeLen):

        del array[mergeIndexs[i]]

if __name__ == '__main__':

       # 加载数据

       data = []

       path = input(r'请输入文件路径：')

       dataSet = load_data(path)

       print(dataSet)

      

       # 进行层次聚类

       k = int(input('请输入聚类次数：'))

       while k-1 > 0:

              result = []

              for indexA,pointsA in enumerate(dataSet):

                     for indexB,pointsB in enumerate(dataSet):

                            if indexB > indexA:

                                   Matrix_min(pointsA,pointsB,indexA,indexB,result)

              mergeIndexs = search_mindis(result)

              mergeGroup(dataSet,mergeIndexs)

              k -= 1

       for item in dataSet:

              print(item)

       ## 可视化

       z=linkage(df,method='ward',metric='euclidean')

       p = dendrogram(z,0)

       plt.show()

---

更多优质内容持续发布中，请移步主页查看。

   点赞+关注,下次不迷路！