[动态规划] (十一) 简单多状态: LeetCode 面试题17.16.按摩师 和 198.打家劫舍
文章目录
- [动态规划] (十一) 简单多状态: LeetCode 面试题17.16.按摩师 和 198.打家劫舍
- 题目分析
- 题目解析
- 状态表示
- 状态转移方程
- 初始化和填表顺序
- 代码实现
- 按摩师
- 打家劫舍
- 总结
注:本题与打家劫舍基本一样,所以只写一道按摩师,末尾只会加上打家劫舍1的代码。
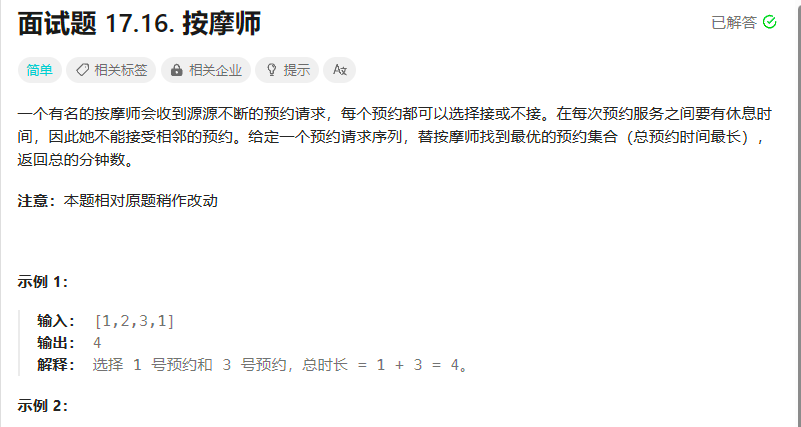
面试题 17.16. 按摩师
198. 打家劫舍
题目分析
(1) 按摩师不能连续接预约
(2) 按摩师可以选择接或者不接预约
(3) 返回预约时间最长的分钟数
题目解析
状态表示
dp[i]:按往常的经验,以i为结尾的最大的服务的分钟数
dp[i]又可以分为:
- f[i]:到
i位置,接第i次预约的服务的最大分钟数 - g[i]:到
i位置,不接第i次预约的服务的最大分钟数
状态转移方程
- f[i]:
f[i]是到i位置,必须接i位置的服务的最大分钟数。
由于不能连续接受服务,所以接了i位置,i-1位置就不能接受预约了。
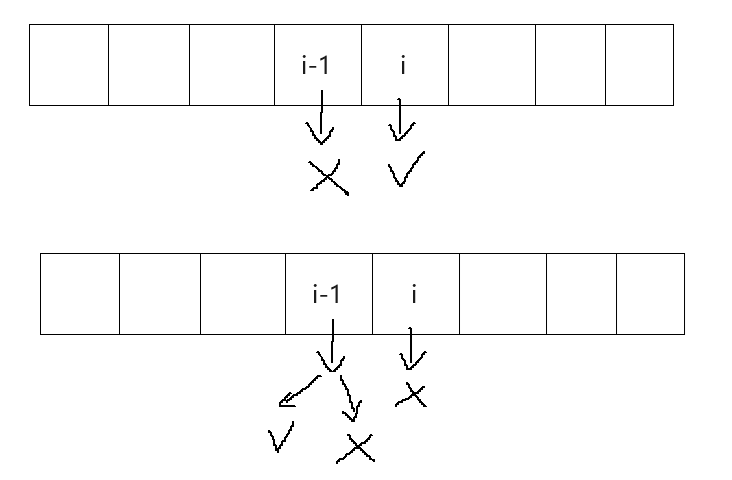
g[i-1]正好是到i-1位置且不接受i-1预约的最大分钟数,再加上对应的i位置的分钟数就是f[i]。(可以参考后面的图)
f[i] = g[i-1] + nums[i]
- g[i]:
g[i]是到i位置,不接i位置的服务的最大分钟数。
由于不接i位置,所以只能看i-1位置。而i-1位置也分为接或者不接。
接i-1位置为f[i-1] (参考状态表示),不接i-1为g[i-1] (参考状态表示)。
由于求最大值,取它们两个较大的值即可。(可以参考后面的图)
g[i] = max(f[i-1], g[i-1])
初始化和填表顺序
- 初始化
- 访问
i-1,所以一般初始化前面的位置。
i == 0时,参考状态表示
f[0] = nums[0], g[0] = 0
- 填表顺序
从左向右填表。
看到这里,大家可以尝试实现代码,再来看接下来的内容。
代码实现
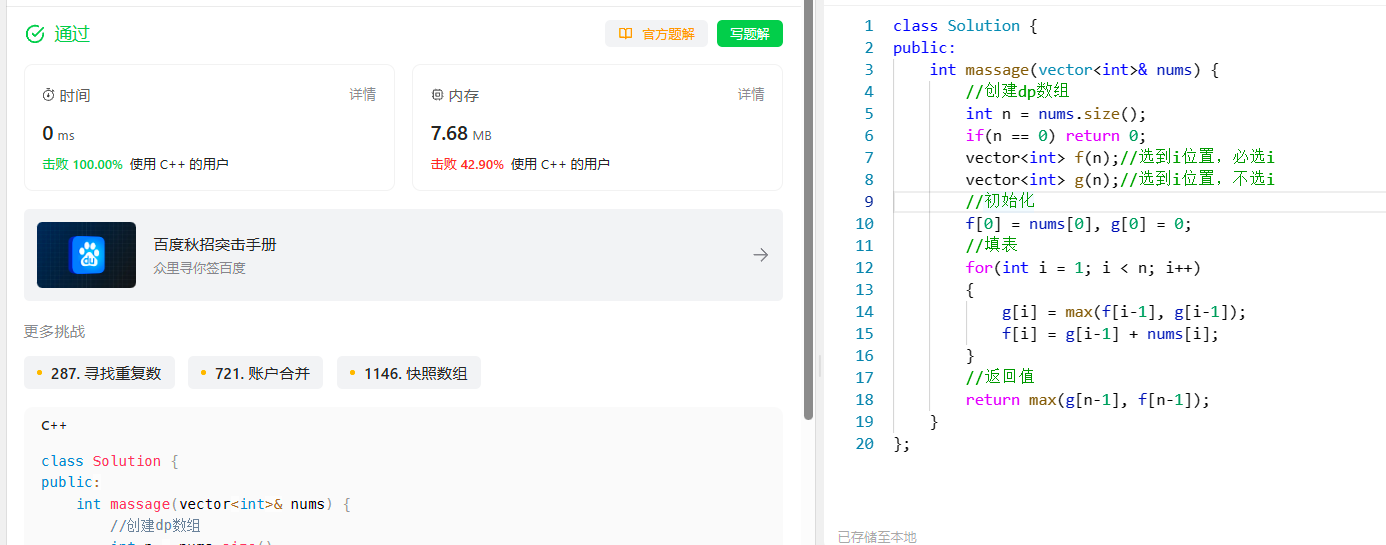
按摩师
class Solution {
public:
int massage(vector<int>& nums) {
//创建dp数组
int n = nums.size();
if(n == 0) return 0;
vector<int> f(n);//选到i位置,必选i
vector<int> g(n);//选到i位置,不选i
//初始化
f[0] = nums[0], g[0] = 0;
//填表
for(int i = 1; i < n; i++)
{
g[i] = max(f[i-1], g[i-1]);
f[i] = g[i-1] + nums[i];
}
//返回值
return max(g[n-1], f[n-1]);
}
};
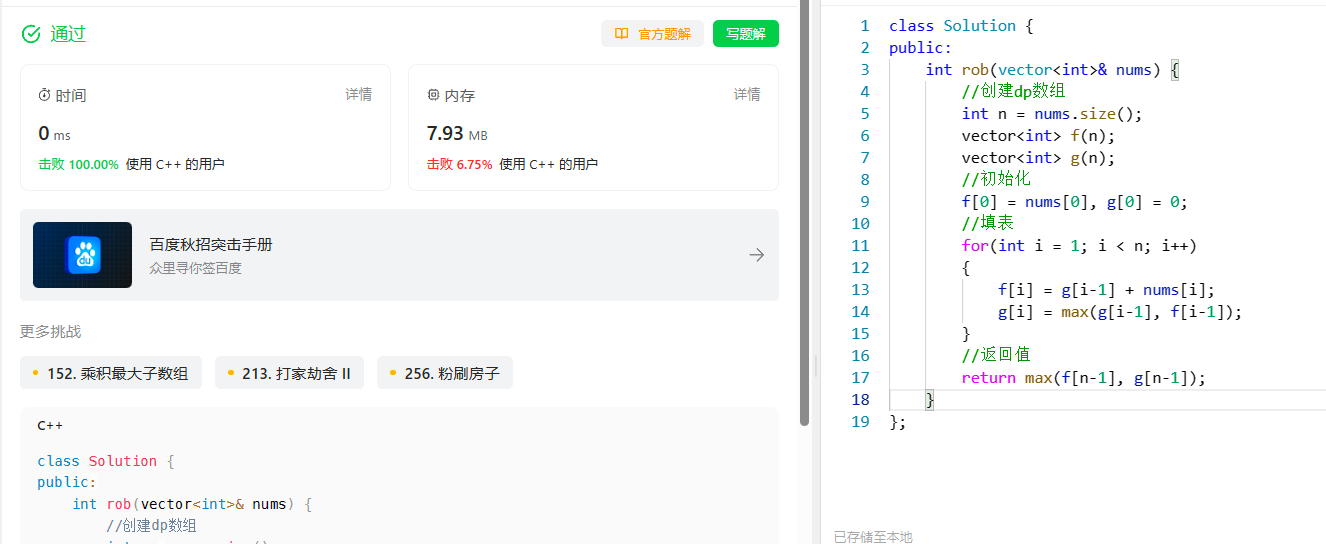
打家劫舍
class Solution {
public:
int rob(vector<int>& nums) {
//创建dp数组
int n = nums.size();
vector<int> f(n);
vector<int> g(n);
//初始化
f[0] = nums[0], g[0] = 0;
//填表
for(int i = 1; i < n; i++)
{
f[i] = g[i-1] + nums[i];
g[i] = max(g[i-1], f[i-1]);
}
//返回值
return max(f[n-1], g[n-1]);
}
};
总结
细节:注重将问题细分,加上画图理解即可。







![【NLP】特征提取: 广泛指南和 3 个操作教程 [Python、CNN、BERT]](https://img-blog.csdnimg.cn/img_convert/7d4a81ef947b615bdc05f5a4d4087c34.jpeg)

