//AVL搜索树
//对数据的搜索: 1:暴力查找遍历
// 2:二叉树 有序,但是伴随着插入删除,维护成本很高
// 3:二叉搜索树 问题:在极端情况下,会退化成最开始的链表
// 4:二叉高度平衡搜索树 AVL树/红黑树
template <typename Key, typename Value>
struct AVLTreeNode
{
pair < Key, Value > _kv;
int _bf; //balance factor 平衡因子
AVLTreeNode<Key, Value>* _left;
AVLTreeNode<Key, Value>* _right;
AVLTreeNode<Key, Value>* _parent;
AVLTreeNode(const pair<Key, Value>& kv)
:_kv(kv)
, _bf(0)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
{ }
};
template <typename Key, typename Value>
class AVLTree
{
typedef AVLTreeNode<Key, Value> Node;
public:
bool insert(const pair<Key, Value>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
//插入数据
Node* cur = _root;
Node* parent = cur;
while (cur)
{
parent = cur;
if (kv.first == cur->_kv.first)
{
return false;
}
else if (kv.first > cur->_kv.first)
{
cur = cur->_right;
}
else if (kv.first < cur->_kv.first)
{
cur = cur->_left;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//更新平衡因子
//1:平衡因子,结点的右子树的高度减去左子树的高度,新增节点cur在右边时,父节点平衡因子++,反之--;
//2:平衡因子为0时,表示树的和高度没有变化,不会影响起祖先
//3:平衡因子为1/-1时,表示parent的树高度有变化,会影响其祖先
while (parent)
{
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
if (parent->_bf == 0)//不会影响祖先,直接更新完毕
{
break;
}
else if (abs(parent->_bf) == 1)//平衡因子为1 / -1时,表示parent的树高度有变化,会影响其祖先
{
cur = parent;
parent = parent->_parent;
}
else if (abs(parent->_bf) == 2)//4:平衡因子为2/-2时,表示parent的树高度已经需要旋转,降低树的高度
{
//左单旋parent平衡因子为2,右高左低,单边cur为1,将cur为1的结点作为新的父节点,原先的父界点作cur的子节点
if (parent->_bf == 2 && cur->_bf == 1)//左单旋
{
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1) //右单旋
{
RotatelR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1) //预处理右旋+左单旋
{
RotatelRL(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1) //预处理左单旋+右旋
{
RotatelLR(parent);
}
}
else//4:平衡因子既不是0,也不是1,-1,不是2,-2时,表示程序;已经出现了bug
{
assert(false);
}
}
return true;
}
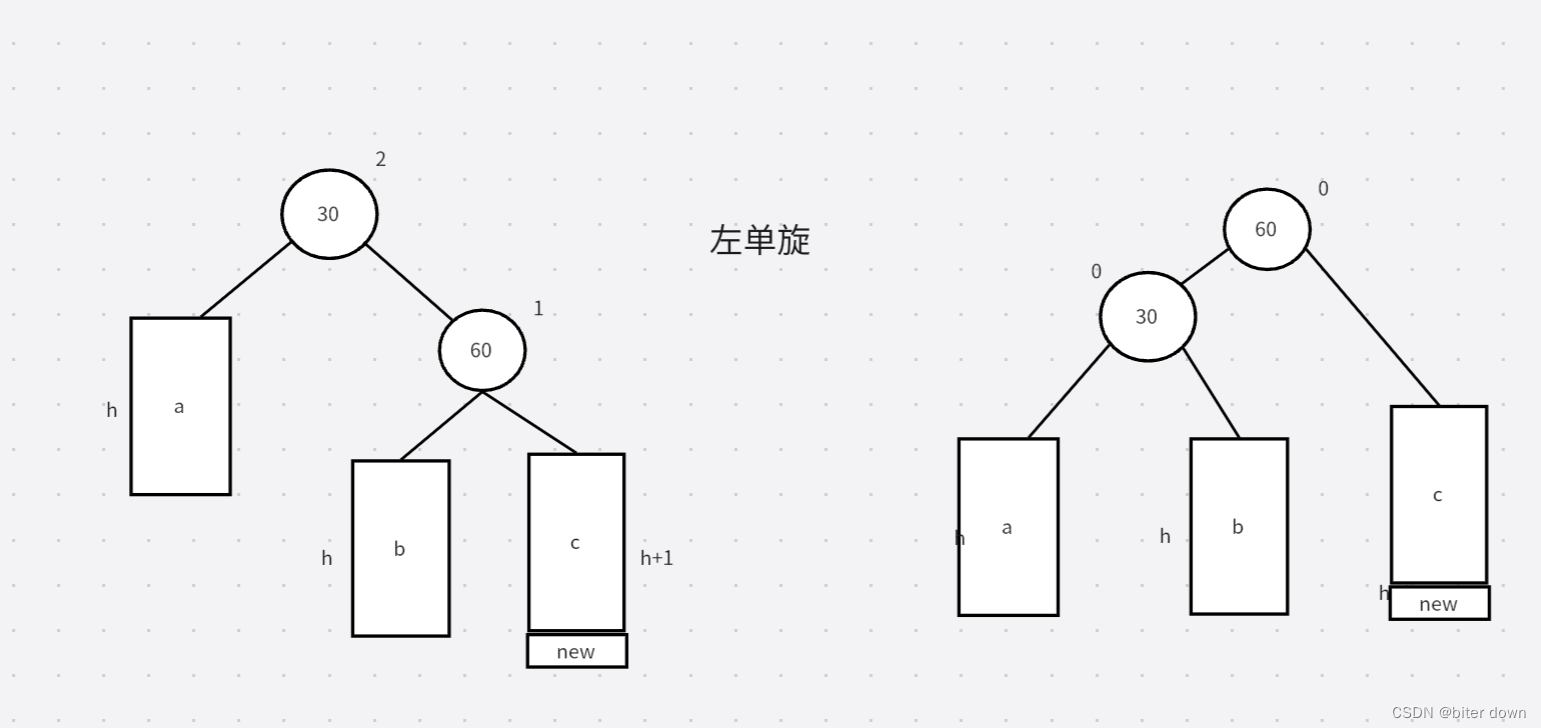
void RotateL(Node*& parent) //左单旋 调整父子节点树中顺序,建立链接(parent与cur,parent的parent与cur),调整平衡因子
{
Node* cur = parent->_right;
Node* cur_left = cur->_left;
parent->_right = cur_left;//将cur的左节点放入parent的右结点
if (cur_left)
{
cur_left->_parent = parent; //cur_left控制_parent
}
cur->_left = parent;//将parent放入cur的左节点
Node* ppNode = parent->_parent;
cur->_parent = parent->_parent; //cur的父节点为原parent的父亲
parent->_parent = cur; //parent的父节点为cur
if (parent == _root) //建议原先父节点的父节点与cur的链接
{
_root = cur;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = cur;
}
else
{
ppNode->_right = cur;
}
}
parent->_bf = cur->_bf = 0;
}
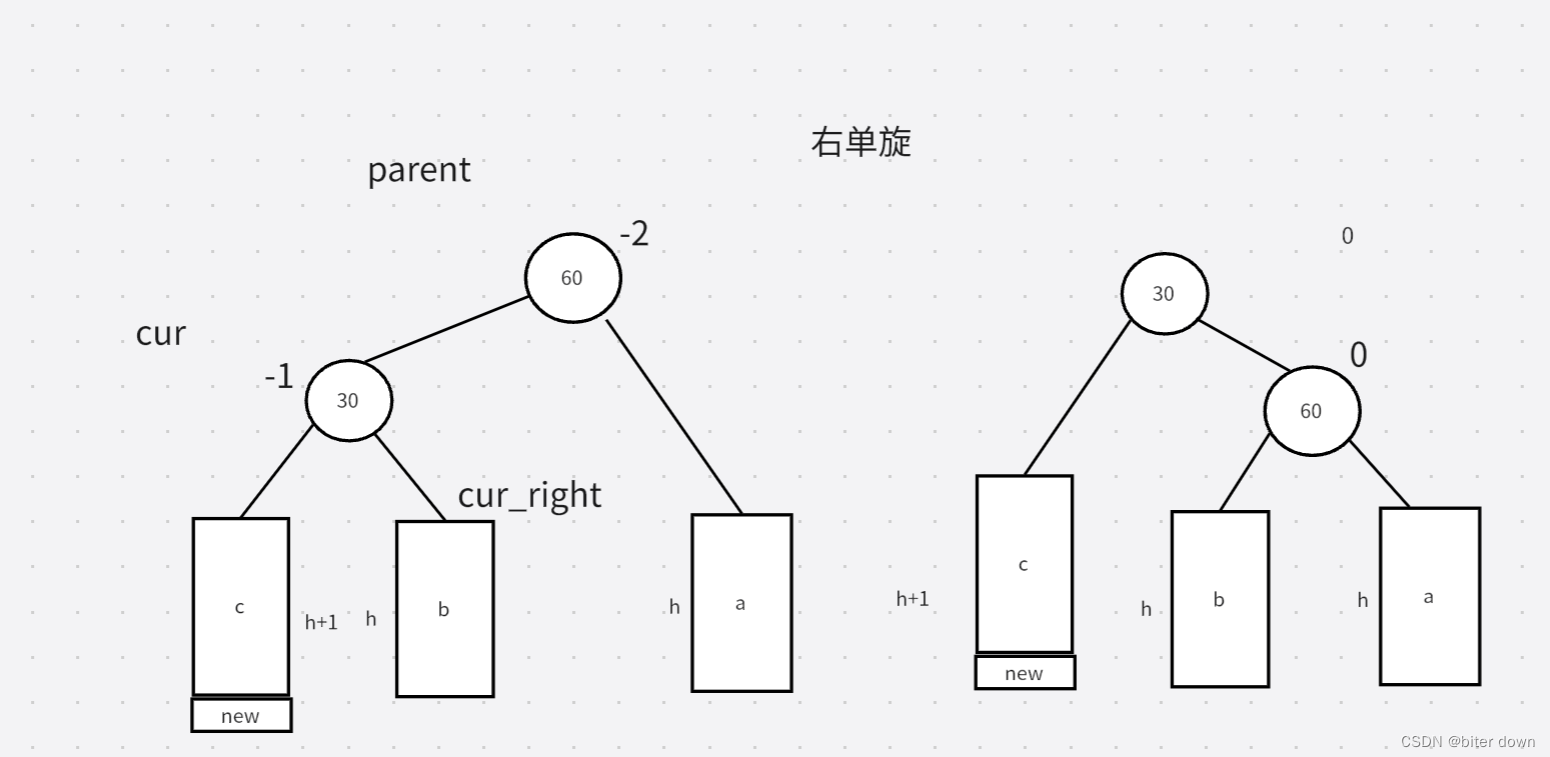
void RotatelR(Node*& parent) //右单旋 调整父子节点树中顺序,建立链接(cur_right(?空)与parent,parent与cur,parent的parent(root?)与cur),调整平衡因子
{
Node* cur = parent->_left;
Node* cur_right = cur->_right;
parent->_left = cur_right;//1:将cur的右节点放入parent的左结点
if (cur_right)
{
cur_right->_parent = parent; //cur_right控制_parent
}
cur->_right = parent;//2:将parent放入cur的右节点
Node* ppNode = parent->_parent;
cur->_parent = parent->_parent; //cur的父节点为原parent的父亲
parent->_parent = cur; //parent的父节点为cur
if (parent == _root) //建议原先父节点的父节点与cur的链接
{
_root = cur;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = cur;
}
else
{
ppNode->_right = cur;
}
}
parent->_bf = cur->_bf = 0;
}
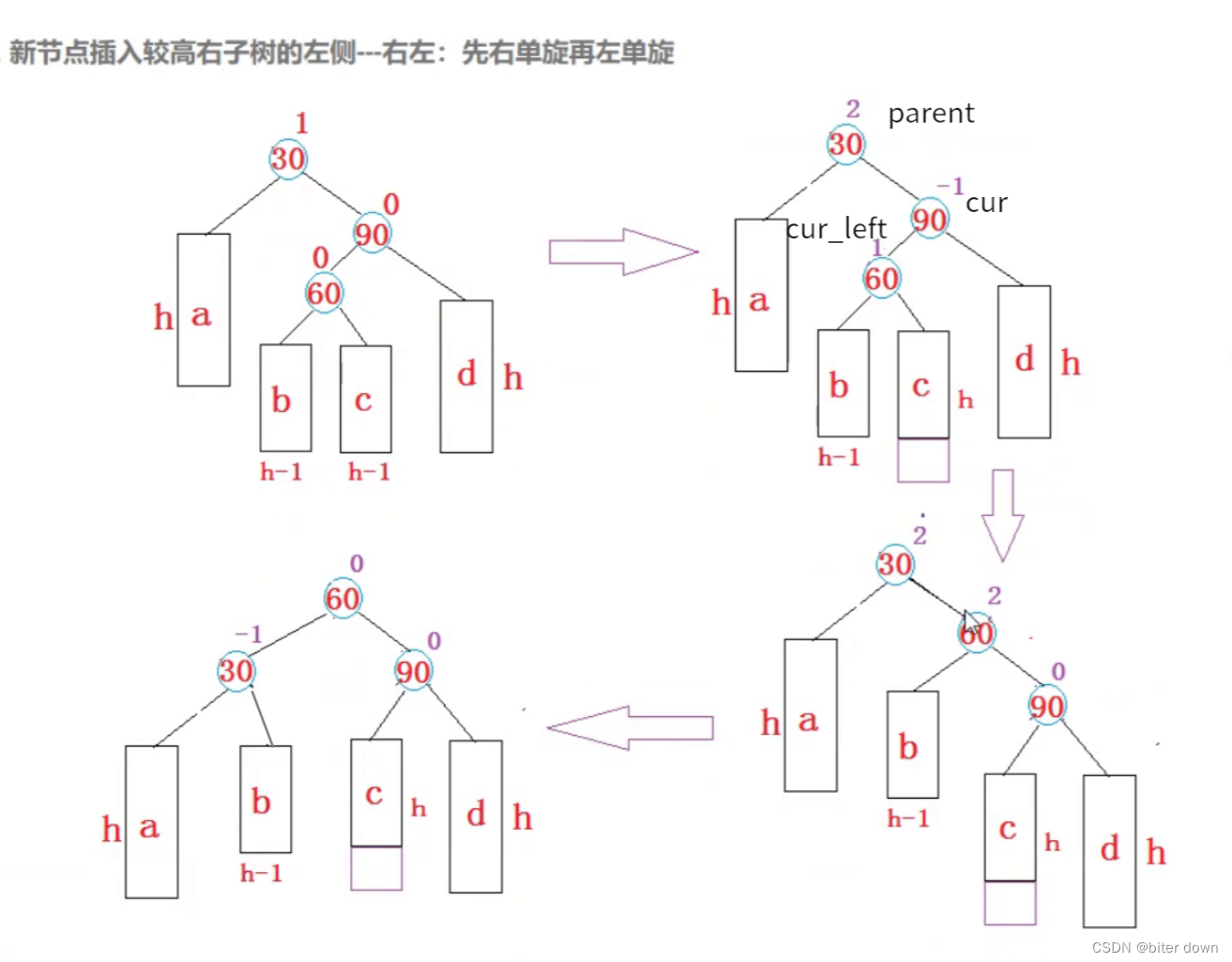
void RotatelRL(Node*& parent) //预处理右旋+左单旋
{
Node* cur = parent->_right;
Node* cur_left = cur->_left;
int bf = cur_left->_bf;
RotatelR(parent->_right);
RotateL(parent);
if (bf == 1)
{
parent->_bf = -1;
}
if (bf == -1)
{
cur->_bf = 1;
}
}
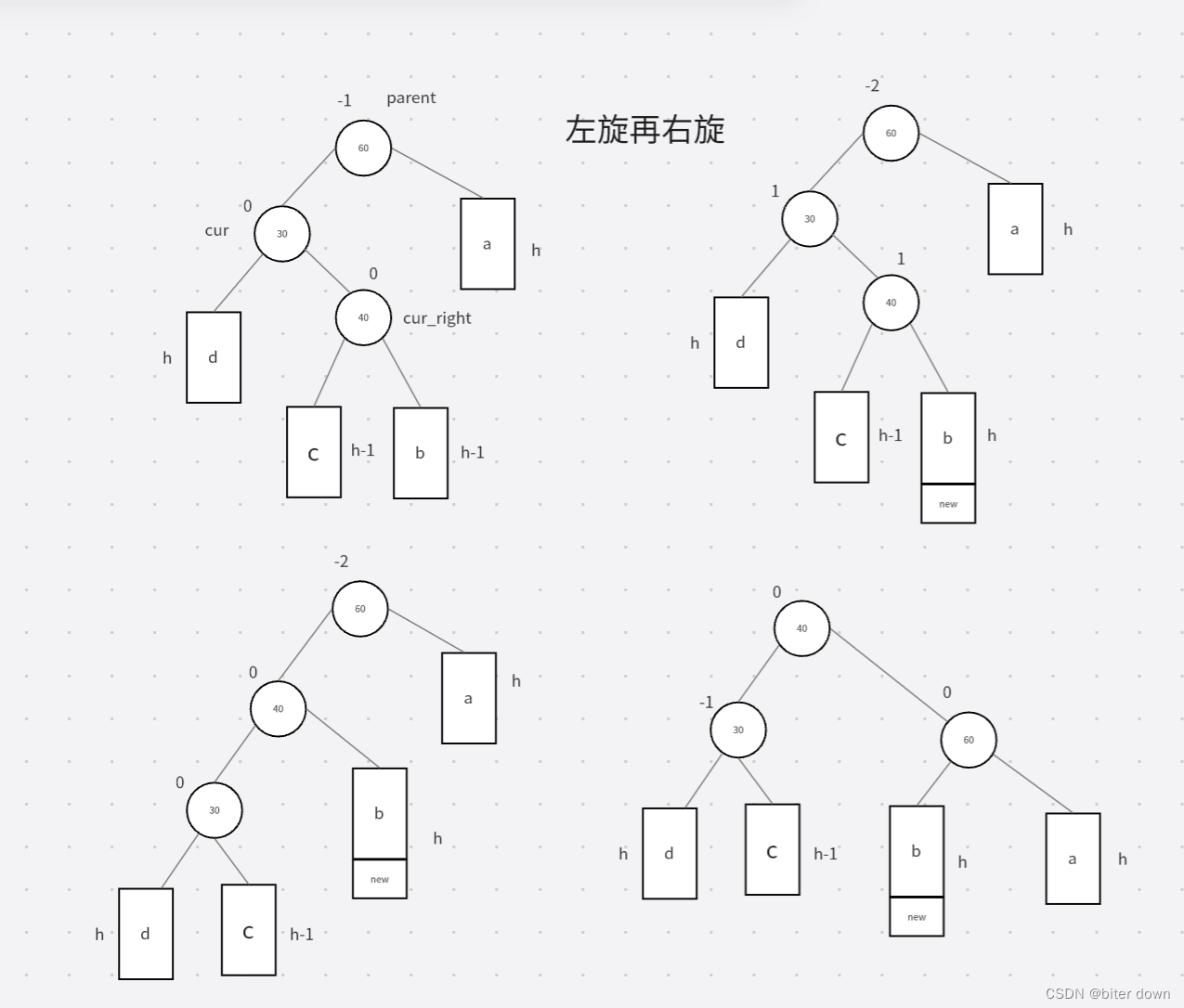
void RotatelLR(Node*& parent) //预处理左单旋+右旋
{
Node* cur = parent->_left;
Node* cur_right = cur->_right;
int bf = cur_right->_bf;
RotateL(cur);
RotatelR(parent);
if (bf == 1)
{
cur->_bf = -1;
}
if (bf == -1)
{
parent->_bf = 1;
}
}
//判断调试AVl平衡代码
//int Height(Node* root) //树的高度
//{
// if (root == nullptr)
// return 0;
// int leftHeight = Height(root->_left);
// int rightHeight = Height(root->_right);
// return leftHeight > rightHeight ? leftHeight++ : rightHeight++;
//}
//bool isBalance()
//{
// return _isBalance(_root);
//}
//bool _isBalance(Node* root) //root为私有节点
//{
// if (root == nullptr)
// return true;
//
// int leftHight = Height(root->_left);
// int rightHight = Height(root->_right);
// //检查平衡因子
// if (rightHight - leftHight != root->_bf)
// {
// cout << "_bf:error:" << root->_kv.first << "factual:" << rightHight - leftHight << "now" << root->_bf << endl;
// return false;
// }
// return abs(rightHight - leftHight)<2
// && isBalance(root->_left)
// && isBalance(root->_right)
//}
private:
Node* _root = nullptr;
};