1. 题目链接:22. 括号生成
2. 题目描述:
数字
n代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。示例 1:
输入:n = 3 输出:["((()))","(()())","(())()","()(())","()()()"]示例 2:
输入:n = 1 输出:["()"]提示:
1 <= n <= 8
3. 解法(递归):
3.1 算法思路:
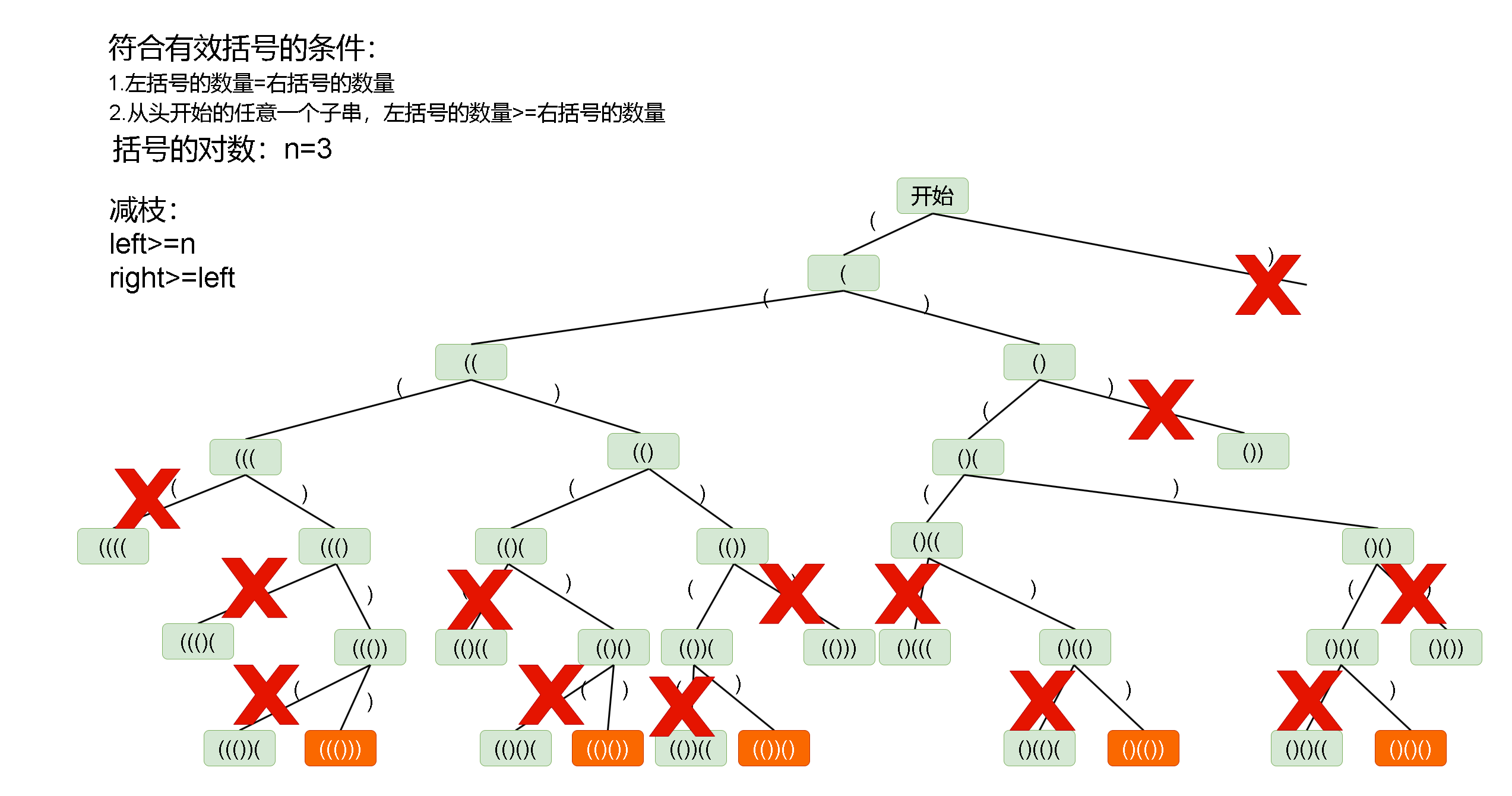
从左往右进行递归,在每个位置判断放置左右括号的可能性,若此时放置左括号合理,则放置右括号继续进行递归,右括号同理
一种判断括号是否合法的方法:从左往右遍历,左括号的数量始终大于等于右括号的数量,并且左括号的总数量与右括号的总数量相等,因此我们在递归时需要进行以下判断:
- 放入左括号时需判断此时左括号的数量是否小于字符串总长度的一半(若左括号的数量大于等于字符串长度的一半时继续放置左括号,则左括号的总数量一定大于右括号的总数量)
- 放入右括号时需要判断此时右括号数量是否小于左括号数量
3.2 递归流程:
-
递归结条件:当前状态字符串长度为2*n相等,记录当前状态并返回
-
若此时左括号数量小于字符串总长度的一半,则在当前状态的字符串末尾添加左括号并继续递归,递归结束撤销添加操作
-
若此时右括号的数量小于左括号的数量(右括号的数量可以由当前状态的字符串长度减去左括号数量求得),则当前状态的字符串末尾添加右括号并递归,递归结束撤销添加操作
3.3 C++算法代码:
class Solution {
int left, right, n; // 定义三个变量:left表示左括号的数量,right表示右括号的数量,n表示总的括号对数
string path; // 定义一个字符串变量path,用于存储当前生成的括号组合
vector<string> ret; // 定义一个字符串向量ret,用于存储所有有效的括号组合
public:
vector<string> generateParenthesis(int _n) {
n = _n; // 将输入的总括号对数赋值给n
dfs(); // 调用深度优先搜索函数来生成括号组合
return ret; // 返回所有有效的括号组合
}
void dfs() {
if (right == n) { // 如果右括号的数量等于总的括号对数,说明已经生成了一个完整的括号组合
ret.push_back(path); // 将当前生成的括号组合添加到结果向量中
return; // 结束当前递归调用
}
if (left < n) { // 如果左括号的数量小于总的括号对数,可以继续添加左括号
path.push_back('('); // 添加左括号到路径中
left++; // 更新左括号的数量
dfs(); // 递归调用dfs函数,继续生成括号组合
path.pop_back(); // 回溯,移除最后一个添加的左括号
left--; // 更新左括号的数量
}
if (right < left) { // 如果右括号的数量小于左括号的数量,可以继续添加右括号
path.push_back(')'); // 添加右括号到路径中
right++; // 更新右括号的数量
dfs(); // 递归调用dfs函数,继续生成括号组合
path.pop_back(); // 回溯,移除最后一个添加的右括号
right--; // 更新右括号的数量
}
}
};