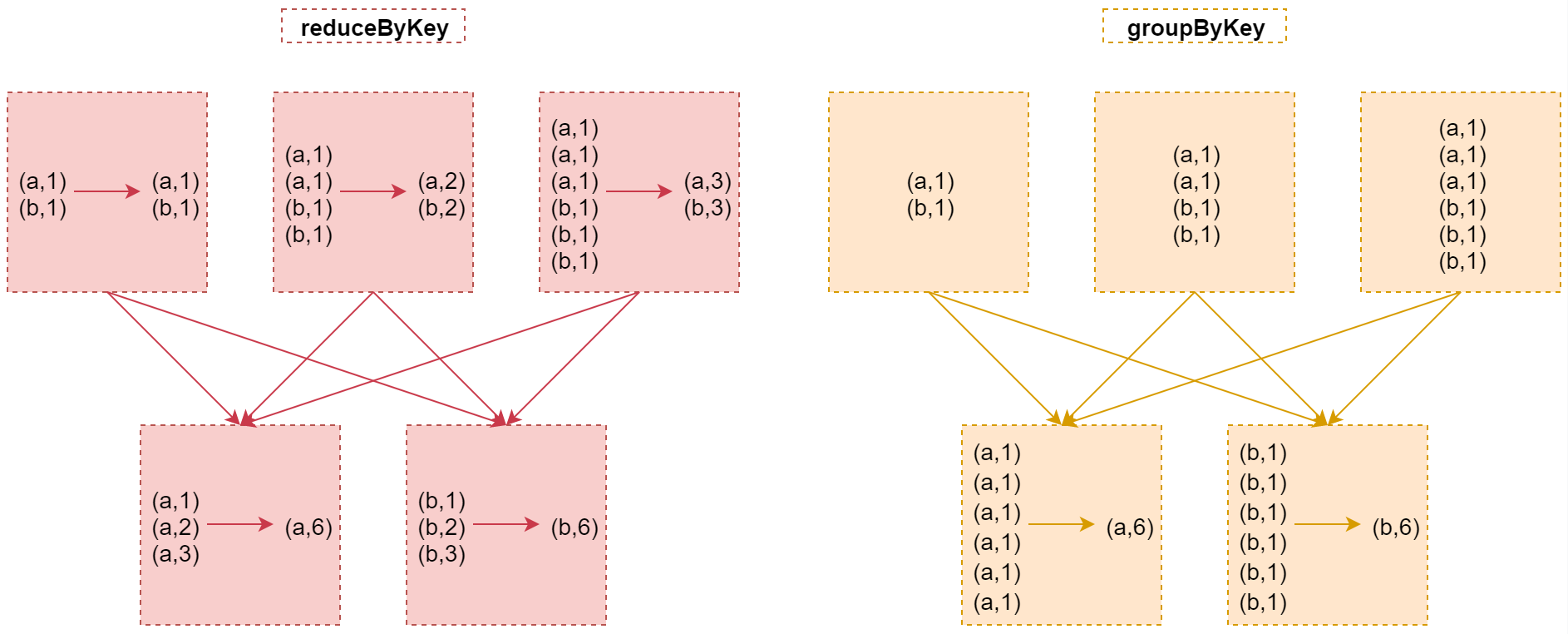
Max-Cut问题简单地说,就是求一种分割方法。给定一张无向图, 将所有顶点分割成两群, 同时使得被切断的边数量最大,或边的权重最大。
QUBO(Quadratic Unconstrained Binary Optimization)问题即二次无约束二值优化问题,将一个传统问题转为QUBO问题建模需要重点关注三部分:
①把建模对象中的变量映射为binary(0/1或者-1/+1)的变量;
②原模型的约束条件需要“处理”到目标函数中,成为无约束问题;
③模型变量的最高次不超过二次。
我们先从简单的问题开始说明,让大家有些直观感受。Max-Cut问题就是一个非常简单,并容易理解的例子。同时Max-Cut问题无需复杂的操作,其模型本身就是QUBO问题。
最大割问题是一类NP难问题,它在计算机科学和组合优化领域中有着广泛的应用。在量子计算领域,最大割问题是一个非常重要的Benchmark,因为它是量子计算机中最具代表性的NP难问题之一,也是许多量子算法的基础。同时,最大割问题在实际应用中有着广泛的应用,如社交网络分析、电路设计、图像分割等领域。因此,通过研究量子算法解决最大割问题,可以为这些领域提供更高效的解决方案。
在量子计算行业中,不同公司往往将Max-Cut问题作为基础案例进行测试,用于算力的对比测试,而经典计算中的很多代表性企业等都曾使用Max-Cut来做新品算力的标定。如英伟达公司使用 896 个 GPU 模拟 1688 个量子比特,能够处理包含高达 3375 个顶点的图最大割问题,Quantinuum 研究团队通过在20量子比特的Quantinuum H1-1量子处理器上进行实验,可解决80个顶点的最大割问题。
2023年5月16日,北京玻色量子科技有限公司(以下简称“玻色量子”)的CTO魏海博士在首场新品发布会现场,就提出了Max-Cut是实用量子计算的“算力标准”🔗。

Max-Cut问题是实用量子计算的“算力标准”
魏海博士提到,在实际问题求解中,玻色量子自研的相干光量子计算机真机——“天工量子大脑”,适用于高效求解组合优化问题,其中最具代表性的21个NP-Complete模型(简称“NPC”)在我们的生活中无处不在。这些问题之间可以互相归约转化,技术中经常用Max-Cut问题来做统一的数学表达,表征计算复杂度。因此,为了标定量子计算的算力优势,我们采用在经典计算中和量子计算中都通用的Max-Cut问题来作为实用量子计算的“算力标准”。
那么,为了更清楚的理解最大割问题,并彻底揭开它的“神秘面纱”,下面将通过案例对该问题在模型层面进行全面解读。
问题描述
最大割问题是NP完备问题。给定一张图, 求一种分割方法, 将所有顶点分割成两群, 同时使得被切断的边数量最大,或边的权重最大。
由于二元变量存在(0/1或者-1/+1)表达形式的区别,常见模型有两种建模思路,在这里分别进行说明。
建模思路一
在无向图G(V,E)中,V为网络的顶点集合,E为网络的边集,其中点i,j∈V,(i,j)∈E,wij为顶点i,j间的边的邻接矩阵,有连边关系则取1,无连边关系则取0。决策变量σi,σj表示顶点i,j的分类,其可能的取值为{1,-1},我们将V划分为A、B两类。

则在给定的无向图中,将所有顶点分割成两群的分割方法所对应割取的边的个数为Z,模型表示为:
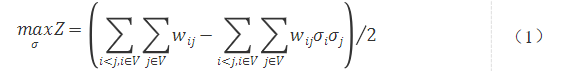
式(1)即为Max-Cut最大割问题模型,同时其也是QUBO模型。
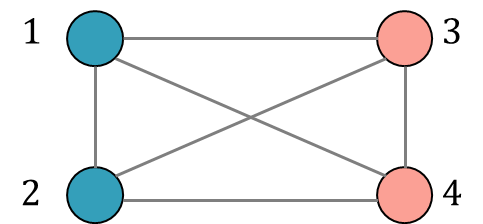
图1:Max-Cut问题实例
为描述该案例,本文以一个四节点实例说明,如图1所示,通过观察我们发现将1、2分为A类,3、4分为B类的“割”法将得到问题的最优解4,如图2所示,下面我们对这个案例进行分析。
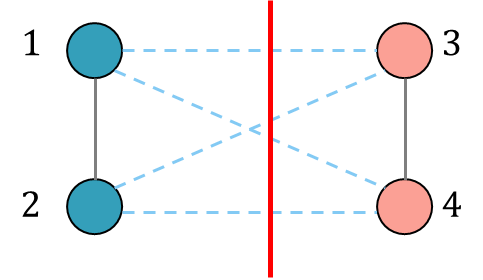
图2:Max-Cut问题“割取”示意
通过连边关系可知


当点1、2为一组,点3、4为一组时,σ1=σ2=1,σ3=σ4=-1。
则式(3)变为

结合式(1)、(2)和(4)可得
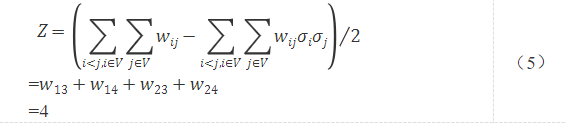
图1的最大割数量为4,符合我们的设想。
当然,这个问题还可以简化,细心的朋友发现wij为系数矩阵,并不影响模型的计算,所以模型式(1)可以转换为求解式(6),式(1)与式(6)在解的取值上是等价的。

同时,式(6)也被理解为一种Ising模型的表达方式。
在该建模思路下,式(1)与式(6)均可理解为Max-Cut最大割问题模型,同时其也是QUBO模型。不同的是,式(1)的目标函数可以表示为割去的边的个数,式(6)的目标函数常用于表示为哈密顿量。
建模思路二
思路1中二元变量通过-1/+1表示,同样我们可以通过0/1变量构建模型,我们用变量xi表示顶点i属于A,B中的某一类。

则在给定的无向图中,将所有顶点分割成两群的分割方法所对应割取的边的个数为Z,模型表示为:
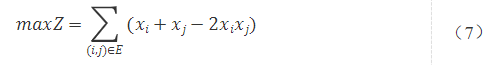
在该建模思路下,式(7)为Max-Cut最大割问题模型,同时其也是QUBO模型。式(7)与式(1)的目标函数可以表示为割去的边的个数。
我们可以试着用QUBO的矩阵表达来描述这个案例。
首先,式(7)等价于式(8)
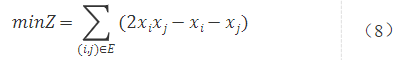
QUBO的矩阵表达式为
![]()
其中,线性项决定了矩阵Q的主对角线上的元素,二次项决定了非对角线上的元素。
以图1中的4节点,6条边的案例为例
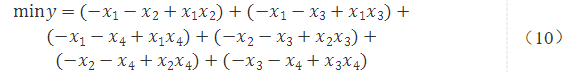
简化后可得
![]()
则Q矩阵表达为
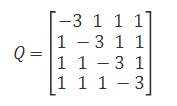
解决这个QUBO模型可以得到x={1,1,0,0}。因此顶点1和2在一个集合中,顶点3和4在另一个集合中,最大切割值为4。
问题拓展
有一个更普遍的问题版本称为加权Max-Cut。在这个问题中,每个边都有一个权重系数,目标函数由最大化边的个数调整为边的总权重之和。
在上述例子中,问题特征直接自然构建了QUBO形式的优化问题。但许多其他问题需要“重铸”来创建所需的QUBO形式。我们将在后面继续介绍其他问题的QUBO建模及其求解。
[参考文献]
[1] GLOVER, FRED, KOCHENBERGER, GARY, DU, YU. Quantum Bridge Analytics I: a tutorial on formulating and using QUBO models[J]. 4OR: Quarterly Journal of the Belgian, French and Italian Operations Research Societies,2019,17(4):335-371. DOI:10.1007/s10288-019-00424-y.
[2] 百度百科
https://baike.baidu.com/item/%E6%9C%80%E5%A4%A7%E5%89%B2%E9%97%AE%E9%A2%98/22910648?fr=aladdin