一、说明
本文探讨贝叶斯模型,首先用摸球游戏展开模型构建步骤,然后讨论分类算法,以及实际操作方法:网格法、二次近似、蒙特卡洛。
二、针对贝叶斯的模型构建
2.1 分支剪枝和假设
在贝叶斯分析中,我们可以将这个过程想象成照料一个充满数据分支路径的花园。这个花园代表了我们考虑的不同可能性或事件顺序。每条路径代表对观察到的数据的不同假设或解释。
当我们收集信息并更多地了解实际发生的情况时,我们开始修剪花园里的树枝。正如园丁移除不需要的植物或树枝一样,我们丢弃与我们收集的数据不一致的替代事件序列。这些修剪过的路径代表了在有证据的情况下不太可能的假设。
最终,通过这个迭代过程,我们的花园中剩下的只是与我们的先验知识和观察到的数据在逻辑上一致的路径。这些剩余的分支代表了与我们所知相符的最合理的解释。通过仔细修剪和选择逻辑一致的路径,我们可以获得一组最能解释观察到的数据的精确假设。
我们探索各种替代事件序列,根据新数据不断更新我们的信念,并有选择地仅保留逻辑上与证据和我们先验知识一致的假设。
2.2 蓝白蓝摸球
让我们想象一下这样的情况:我们有一个袋子,里面有四颗弹珠。弹珠可以有两种不同的颜色,蓝色或白色。我们知道总共有四颗弹珠,但我们缺乏有关袋子内颜色具体分布的信息。
我们已经获得了一些证据:通过反复从袋子中抽取弹珠,一次一个,并在每次抽取后将它们放回袋子中,我们创建了三个弹珠的序列。
首先,让我们关注一个假设。假设袋子里有一颗蓝色大理石和三颗白色大理石。
我们可以想象可能性像树枝一样散开。总共有 64 条潜在路径需要考虑 (4^3=64)。只有 3 个符合我们对袋子中所装物品的假设以及我们收集的数据。
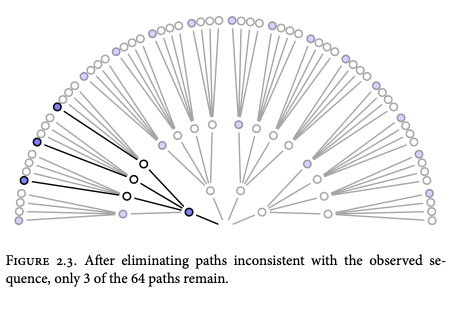
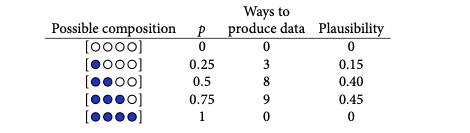
对于每个可能的猜想,产生观察数据的方法:

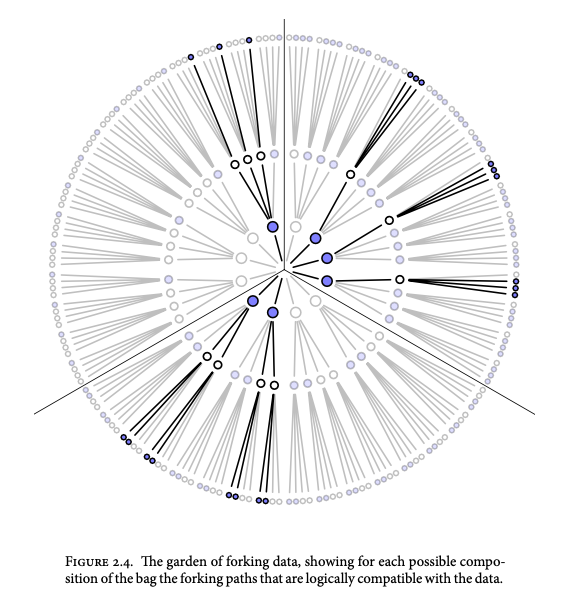
三个蓝色弹珠和一个白色弹珠的组合提供了获得观察序列的最高概率。这些弹珠的初始计数构成了我们的起点,我们随后将对其进行修改或更新。我们将这些初始计数称为“先验计数”。
我们从袋子里取出另一个弹珠,这为我们提供了额外的观察结果:这次是蓝色弹珠。我们获取先前的计数,称为先前计数 (0, 3, 8, 9, 0),并根据新的观察结果更新它们。我们只是根据这些新信息修改先前的计数,而不是推测或做出新的假设。

例如,想象一下大理石工厂的一个人告诉您蓝色大理石不常见。此外,他们还确认每个袋子中至少包含一颗蓝色和一颗白色大理石,这提供了更多信息。根据这一新知识,我们可以再次相应地修改和更新我们的计数。
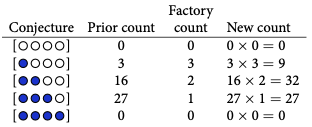
让我们通过标准化合理性来创建概率,使所有可能假设的合理性之和等于 1。为了实现这种标准化,您只需将所有乘积相加,每个乘积对应于p可以假设的潜在值,然后将每个乘积除以乘积的总和。
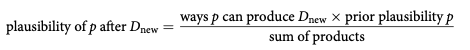
ways = np.array([0, 3, 8, 9, 0])
ways / ways.sum()
# array([0. , 0.15, 0.4 , 0.45, 0. ])- p称为参数值。这只是对数据的可能解释进行索引的一种方式。
- 生成数据的值p的相对频率称为似然度。它是通过考虑所有可能的数据并去除那些与观测数据不一致的数据来确定的。
- 任何特定p的先验合理性就是先验概率。
- 任何特定p的新的、更新的似然性是后验 概率。
想象一下你有一个代表地球的地球仪。您旋转地球仪并在其表面上随机选择一个点。接下来,观察并记录所选点是否对应于水或陆地。
呜呜呜呜呜呜呜呜呜呜
我们有 9 个观测值(6 个水体和 3 个陆地),这个序列就是我们的数据。

为了启动推理过程,我们必须建立某些假设,这些假设构成我们模型的基础。创建基本贝叶斯模型涉及一个由三个步骤组成的设计循环:
- 数据故事:首先构建一个叙述,解释观察到的数据是如何生成的。这个讲故事的过程有助于激发模型并为模型提供背景。
- 更新:继续通过输入可用数据来训练模型。此步骤涉及将观察到的数据合并到模型中,并根据这些新信息更新其信念或参数。
- 评估:与任何统计模型一样,评估和评估其性能至关重要。该评估过程可能会揭示模型是否需要修订或调整,以提高其准确性和实用性。此步骤包括检查模型与数据的拟合度、评估其预测能力以及考虑任何限制或需要改进的领域。
针对我们的具体情况,我们可以通过以下方式构建故事:
p代表水的实际比例。当我们旋转地球仪时,观测到的水的概率为p ,观测到的陆地的概率为1-p 。每个旋转都独立于其他旋转。
在贝叶斯模型开始时,初始合理性被分配给每个可能的结果或假设。这些初始似真性被称为先验似真性。随着新数据的出现,模型会更新这些似真性以生成后验似真性。此更新过程是一种称为贝叶斯更新的学习形式。
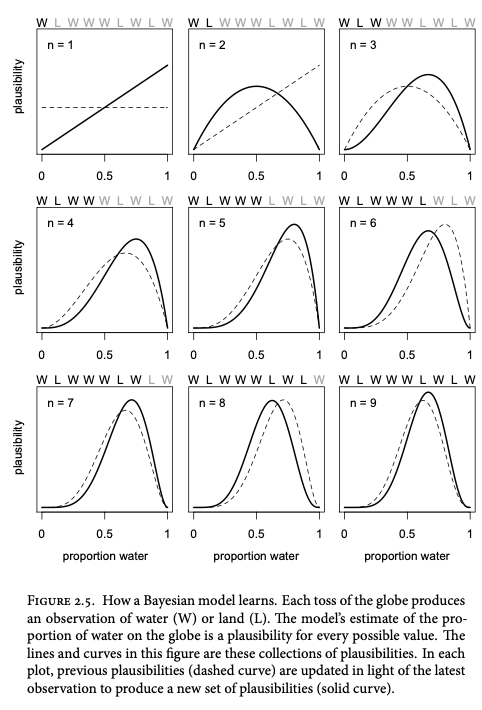
每条虚线代表上一张图中的实线,从左到右、从上到下过渡。每当观察到“W”(代表水)时,似然曲线的峰值就会向较大的p值移动,表明水的比例较大的可能性较高。相反,当观察到“L”(代表土地)时,峰值向相反方向移动,表明p值较小的概率较高,表明土地比例较大。
目前,重要的是要认识到目标不是验证模型假设的绝对真实性。我们知道模型的假设永远不会与实际的数据生成过程完全一致。因此,从这个意义上来说,审查模型是否完全准确或真实是没有意义的。
相反,目的是评估模型对于特定目的的适用性或充分性。这通常涉及提出额外的问题并寻求超出模型原始构造的答案。重点转向评估模型服务其预期目标的效果。
2.3 模型的组成部分
变量是可以具有不同值的符号。第一个感兴趣的变量是p,代表地球上水的比例。p是不可观测的(称为参数),但可以从其他变量推断出来。其他变量是观测到的水和土地数量。
列出变量后,我们必须定义每个变量。在我们的场景中,我们引入两个假设:
- 每次抛掷都独立于其他抛掷,
- 每次抛掷得到水的概率保持不变
概率论提供了一个确定的解决方案,称为二项式分布。
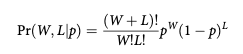
“水”W 和“地”L 的计数呈二项式分布,每次抛掷“水”的概率为 p。
W 和 L 是观测变量。
stats.binom.pmf(6, n=9, p=0.5)
# 0.16406250000000003该stats.binom.pmf()函数计算二项式分布的概率质量函数 (PMF)。PMF 给出了在给定次数的试验(由 指定)中获得特定次数的成功(在本例中为“6”)的概率,n并且每次试验的成功概率(由 指定p)固定。
因此,通过调用stats.binom.pmf(6, n=9, p=0.5),我们计算在 9 次独立试验(旋转)中准确获得 6 次成功(或 6 个水观察结果)的概率,每次试验成功(获得水)的概率为 0.5 (50%)。
probabilities = [stats.binom.pmf(6, n=9, p=(x+1)*0.1) for x in range(10)]
plt.plot(np.arange(0, 1., 0.1), probabilities, 'bo-')
plt.xlabel('Probability (p)')
plt.ylabel('Probability of 6 successes')
plt.title('Probability of 6 successes in 9 trials for different p values')
plt.show()
不同 p 值的概率。图片由作者提供。
我们有参数 p,它表示对水进行采样的概率。p无法直接观察到(未观察到的 变量)。尽管无法观察到,但定义p仍然至关重要。
对于贝叶斯机打算考虑的任何参数,有必要提供表示初始合理性的先验分布。
我们现在可以获得我们的模型。
W ∼ 二项式(N, p)
N 次试验中的 W 概率为p。
p ∼ 均匀(0, 1)
p在其整个可能的范围内具有均匀的(平坦的)先验。
贝叶斯模型能够将所有先验分布更新为其逻辑结果,从而得到后验分布。后验分布表示给定观测数据的参数的概率分布。在这种特殊情况下,我们将其表示为Pr(p|W, L),它表示每个可能值p的概率,以我们所看到的 W 和 L 的具体观察为条件。
后验分布的精确数学定义源于贝叶斯定理的原理。如果您需要复习贝叶斯定理,您可以参阅我之前详细介绍该主题的文章。
三、朴素贝叶斯分类算法
多项式和高斯朴素贝叶斯的解释
![]()
它表示,考虑到数据, p的任何特定值的概率等于以p为条件的数据的相对合理性和p 的先验合理性的乘积除以Pr(W, L),我将其称为数据的平均概率。
![]()
概率 Pr(W, L) 表示观测数据的平均概率,通过对先验分布求平均值来计算。其目的是对后验分布进行归一化或标准化,确保后验分布内的概率总和(或积分)为 1。
![]()
E 是期望。计算连续值分布的平均值,例如p的无限可能值。
贝叶斯模型可以被视为具有预定义组件的机器。它包括一个电机,用于处理数据并通过根据观察到的数据调节先验分布来生成后验分布。
虽然形式条件并不总是可行,但可以引入网格近似、二次近似和马尔可夫链蒙特卡罗等数值技术来近似从贝叶斯定理导出的数学。
这些技术用作计算后验分布的条件引擎,可适应广泛的先验以进行灵活的推理。
四、网格近似
网格近似是贝叶斯推理中的一种简单调节技术。不是考虑无限数量的参数值,而是使用参数值的有限网格来近似连续后验分布。
该过程涉及将先验概率乘以网格中每个参数值的似然度来计算后验概率。
由于参数数量不断增加带来的可扩展性问题,网格近似对于复杂建模来说并不实用。
def posterior_grid_approx(grid_points=5, success=6, tosses=9):
"""
"""
# define grid
p_grid = np.linspace(0, 1, grid_points)
# define prior
prior = np.repeat(5, grid_points) # uniform
#prior = (p_grid >= 0.5).astype(int) # truncated
#prior = np.exp(- 5 * abs(p_grid - 0.5)) # double exp
# compute likelihood at each point in the grid
likelihood = stats.binom.pmf(success, tosses, p_grid)
# compute product of likelihood and prior
unstd_posterior = likelihood * prior
# standardize the posterior, so it sums to 1
posterior = unstd_posterior / unstd_posterior.sum()
return p_grid, posteriorpoints = 20
w, n = 6, 9
p_grid, posterior = posterior_grid_approx(points, w, n)
plt.plot(p_grid, posterior, 'o-', label='success = {}\ntosses = {}'.format(w, n))
plt.xlabel('probability of water', fontsize=14)
plt.ylabel('posterior probability', fontsize=14)
plt.title('{} points'.format(points))
plt.legend(loc=0);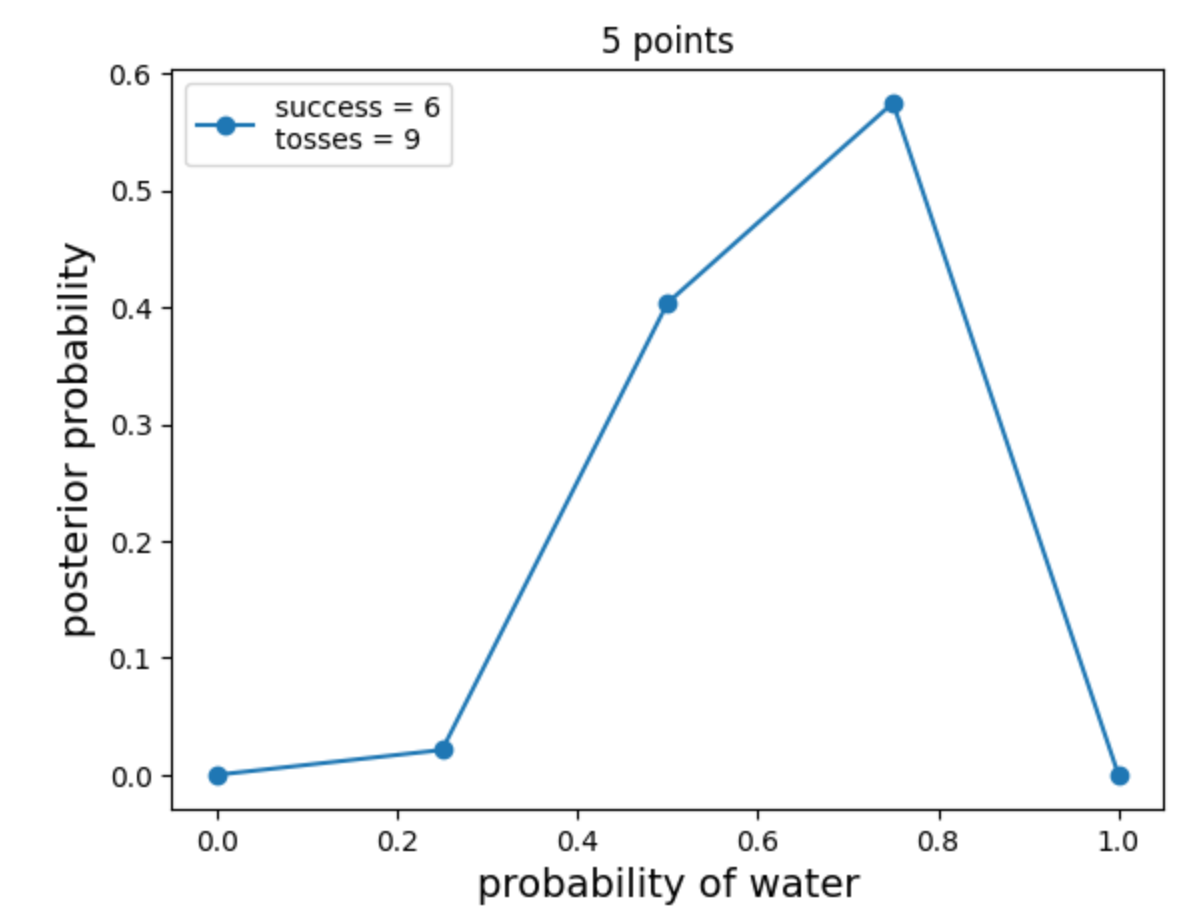
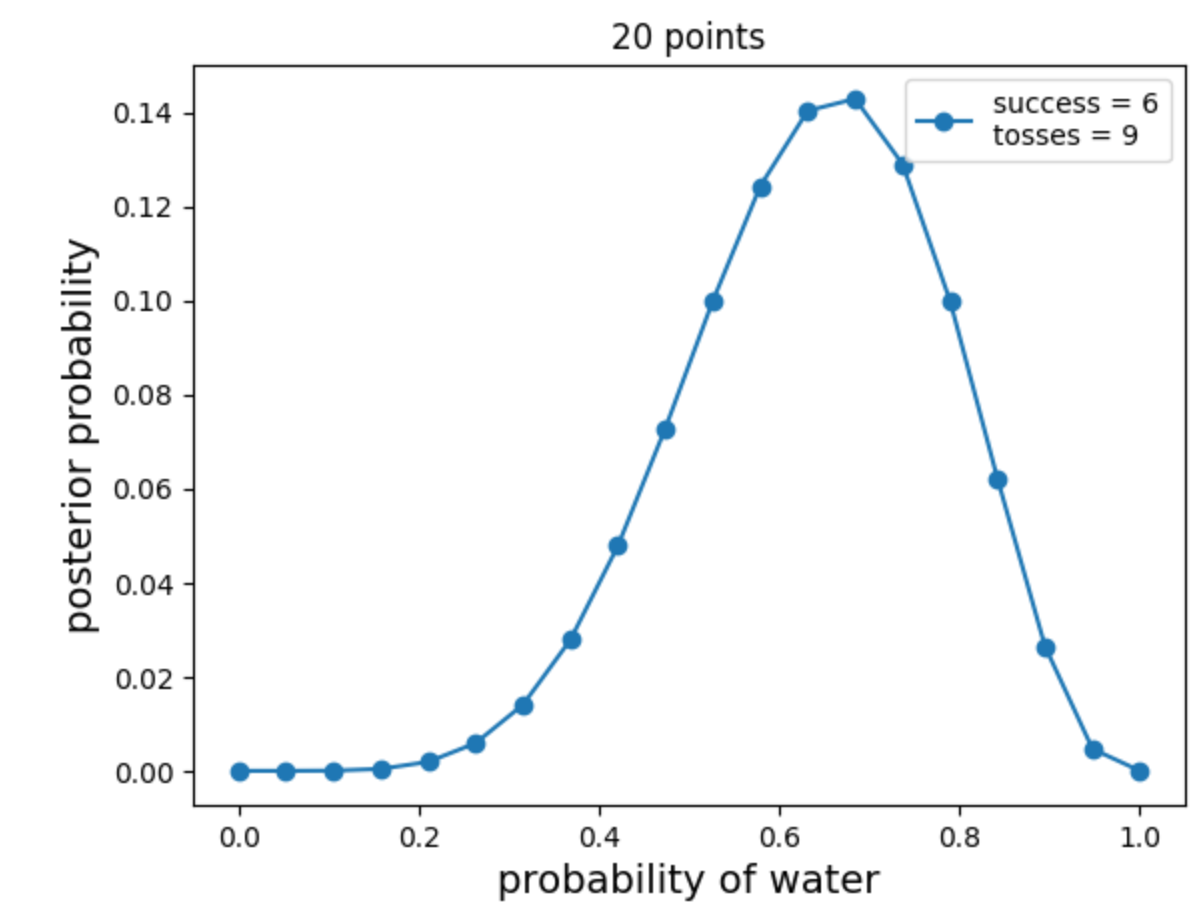
网格近似。图片由作者提供。
五、二次近似
二次近似是贝叶斯推理中的一种有价值的方法。它基于这样的观察:在一般条件下,后验分布的峰值周围的区域非常类似于高斯分布。这种高斯近似通过仅需要两个参数来简化后验分布:均值(中心)和方差(分布)。
“二次近似”一词的出现是因为高斯分布的对数形成抛物线,而抛物线是二次函数。因此,该近似表示使用抛物线形状的后验分布的对数。
通过利用高斯近似,可以用更简单的抛物线表示来有效地近似复杂的后验分布。
data = np.repeat((0, 1), (3, 6))
with pm.Model() as normal_approximation:
p = pm.Uniform('p', 0, 1)
w = pm.Binomial('w', n=len(data), p=p, observed=data.sum())
mean_q = pm.find_MAP()
std_q = ((1/pm.find_hessian(mean_q, vars=[p]))**0.5)[0]
mean_q['p'], std_q
# (array(0.66666667), array([0.15713484]))
# shows the posterior mean value of p = 0.67
# the standard deviation of the posterior distribution 0.16
# Assuming the posterior is Gaussian, it is maximized at 0.67,
# and its standard deviation is 0.16由于我们已经知道后验,让我们比较一下近似值有多好。
norm = stats.norm(mean_q, std_q)
prob = .89
z = stats.norm.ppf([(1-prob)/2, (1+prob)/2])
pi = mean_q['p'] + std_q * z
pi
# array([0.41553484, 0.91779849]) the lower and upper bounds of the confidence interval.通过使用stats.norm.ppf,我们计算与所需概率水平的下尾部和上尾部相对应的 z 分数。该[(1-prob)/2, (1+prob)/2]部分确保我们计算双尾区域的 z 分数。
该pi变量表示值的数组。std_q它通过将标准差 ( ) 乘以先前计算的 z 分数并加上平均值 ( mean_q['p'])来计算置信区间的下限和上限。
# analytical calculation
w, n = 6, 9
x = np.linspace(0, 1, 100)
plt.plot(x, stats.beta.pdf(x , w+1, n-w+1),
label='True posterior')
# quadratic approximation
plt.plot(x, stats.norm.pdf(x, mean_q['p'], std_q),
label='Quadratic approximation')
plt.legend(loc=0, fontsize=13)
plt.title('n = {}'.format(n), fontsize=14)
plt.xlabel('Proportion water', fontsize=14)
plt.ylabel('Density', fontsize=14);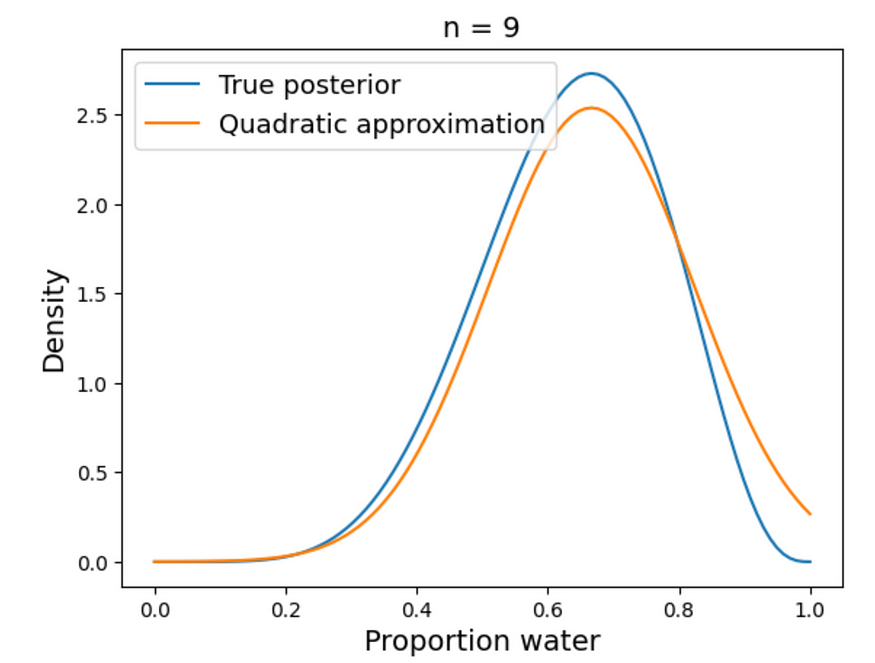
随着数据量的增加,二次逼近的准确性提高。
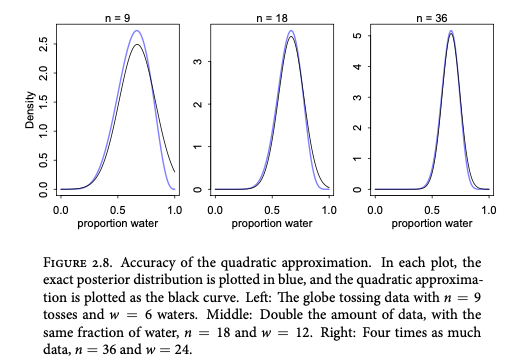
六、马尔可夫链蒙特卡罗
对于复杂模型(例如具有大量参数的多级模型),网格近似和二次近似可能无法令人满意。由于计算限制,网格近似变得不切实际,并且二次近似可能无法很好地拟合模型。此外,多级模型通常缺乏后验分布的统一函数,因此很难找到最大后验(MAP)估计。
为了解决这些问题,马尔可夫链蒙特卡罗(MCMC)作为一种流行的模型拟合技术应运而生。MCMC 是一个能够处理复杂模型的调节引擎系列,在贝叶斯数据分析的兴起中发挥了重要作用。虽然 MCMC 的历史早于 20 世纪 90 年代,但它因经济实惠的计算机能力的可用性而获得了关注。
MCMC 的独特之处在于其从后验分布中采样的策略,而不是直接计算或近似它。通过采样收集一组参数值,这些值的频率代表后验的似然性。后验分布可以通过构建这些样本的直方图来可视化。
参考来源
除非另有说明,本内容中的所有图像和公式均直接源自 Richard McElreath 所著的《统计反思,第二版》一书。 奥坎·耶尼贡