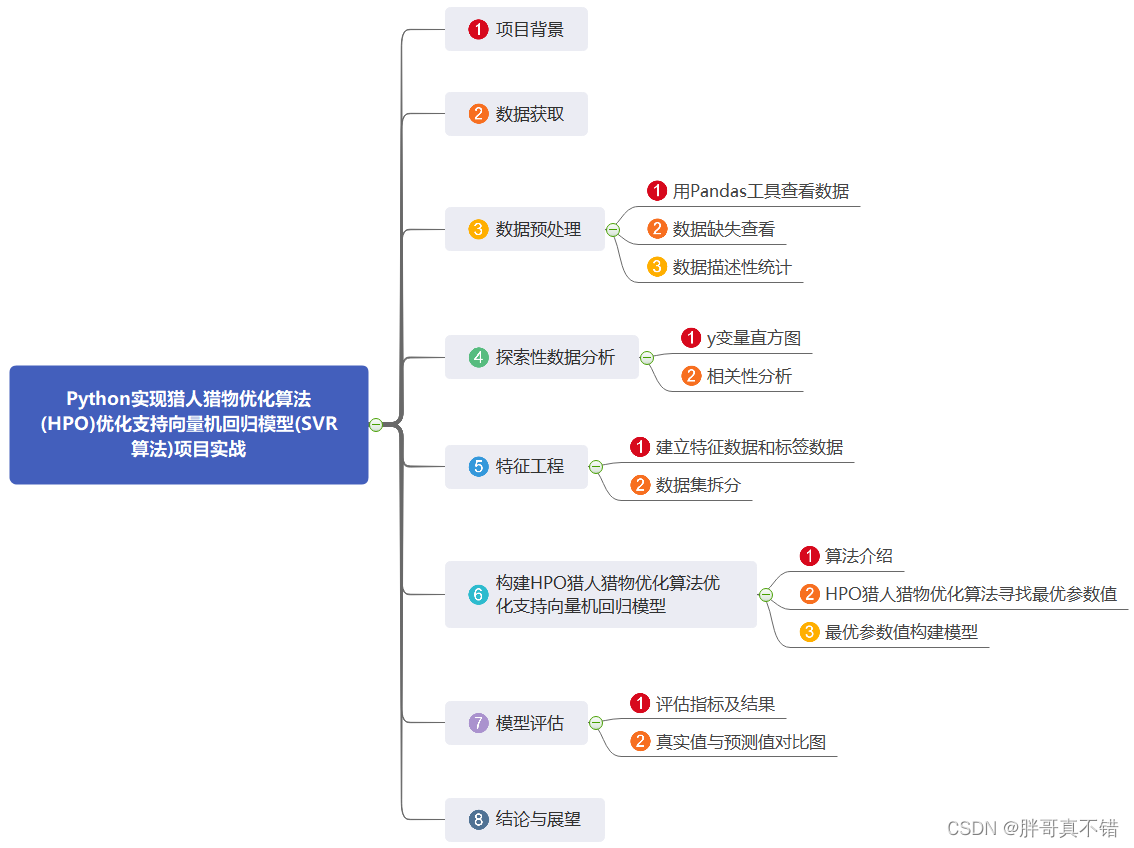
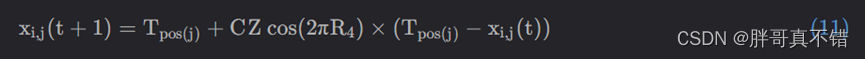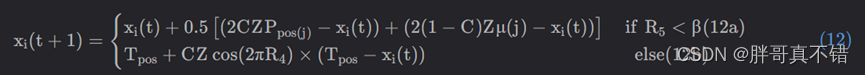说明：这是一个机器学习实战项目（附带数据+代码+文档+视频讲解），如需数据+代码+文档+视频讲解可以直接到文章最后获取。

1.项目背景

猎人猎物优化搜索算法(Hunter–prey optimizer, HPO)是由Naruei& Keynia于2022年提出的一种最新的优化搜索算法。受到捕食动物(如狮子、豹子和狼)和猎物(如雄鹿和瞪羚)的行为的启发，他们根据猎人和猎物的位置移动方法设计了一种新型的搜索方式及自适应度更新的方法。

本项目通过HPO猎人猎物优化算法寻找最优的参数值来优化支持向量机回归模型。

2.数据获取

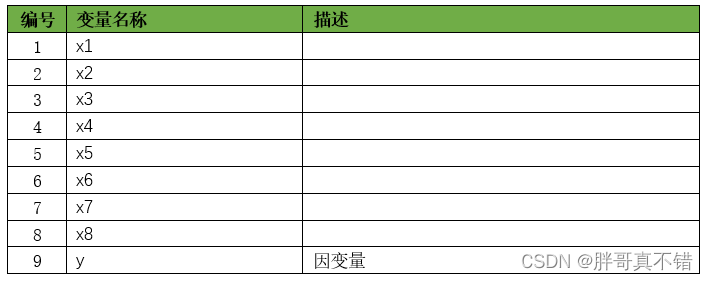
本次建模数据来源于网络(本项目撰写人整理而成)，数据项统计如下：

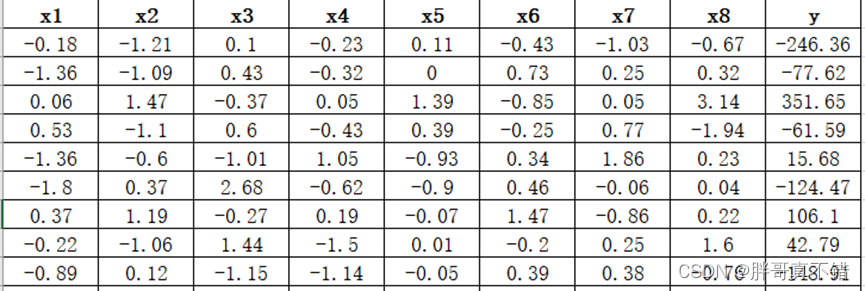
数据详情如下(部分展示)：

3.数据预处理

3.1 用Pandas工具查看数据

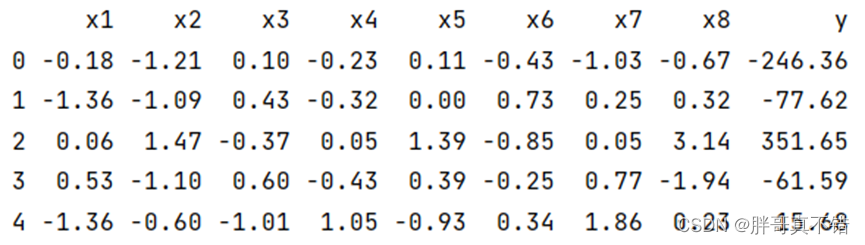
使用Pandas工具的head()方法查看前五行数据：

关键代码：

 

3.2数据缺失查看

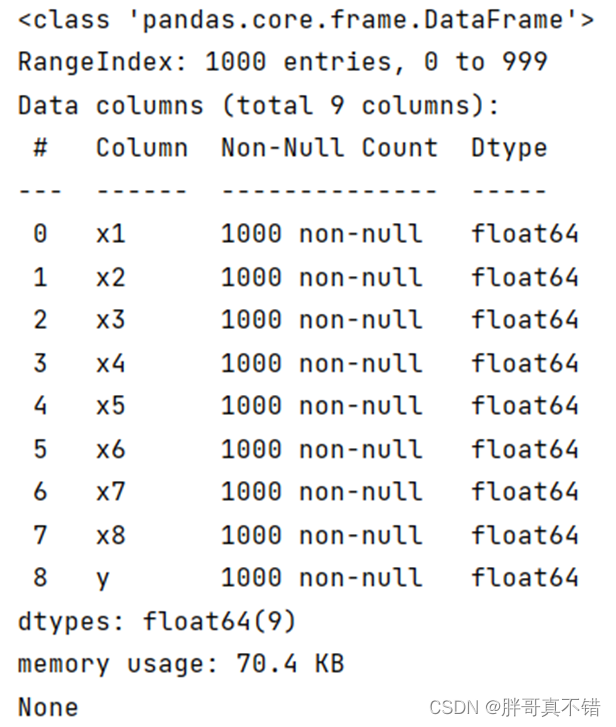
使用Pandas工具的info()方法查看数据信息：

从上图可以看到，总共有9个变量，数据中无缺失值，共1000条数据。

关键代码：

3.3数据描述性统计

通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。

关键代码如下：

 

4.探索性数据分析

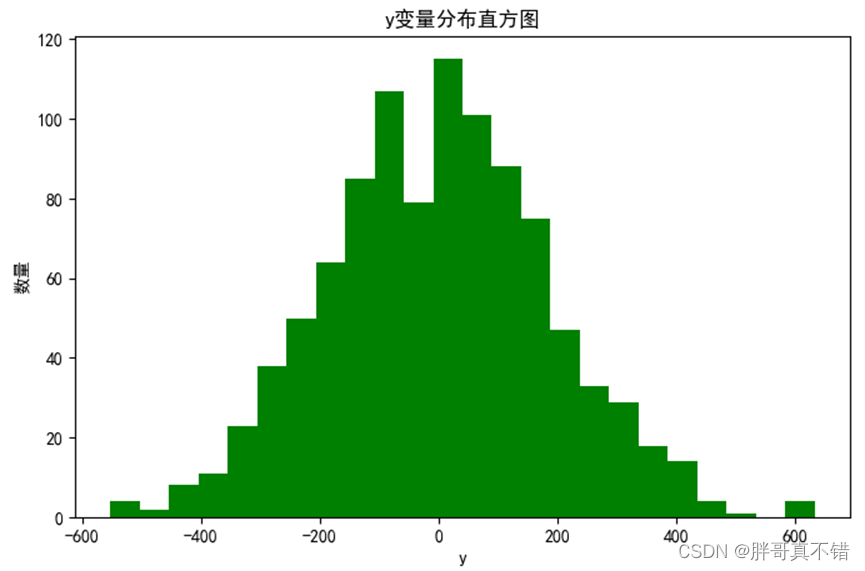
4.1 y变量直方图

用Matplotlib工具的hist()方法绘制直方图：

从上图可以看到，y变量主要集中在-200~200之间。

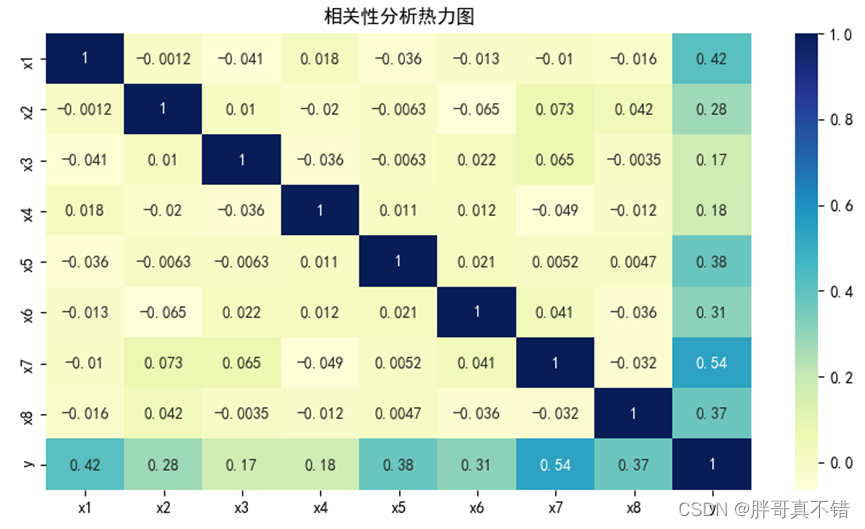
4.2 相关性分析

从上图中可以看到，数值越大相关性越强，正值是正相关、负值是负相关。

5.特征工程

5.1 建立特征数据和标签数据

关键代码如下：

5.2 数据集拆分

通过train_test_split()方法按照80%训练集、20%测试集进行划分，关键代码如下：

6.构建HPO猎人猎物优化算法优化支持向量机回归模型

主要使用HPO猎人猎物优化算法优化SVR算法，用于目标回归。

6.1 算法介绍

     说明：HPO算法介绍来源于网络，供参考,需要更多算法原理，请自行查找资料。

算法原理：

首先，将初始总体随机设置为→x={→x1,→x2,…,→xn} ，然后将种群总体所有成员的目标函数计算为→O={O1,O2,…,On} 。受该算法启发，通过一系列规则和策略在搜索空间中控制和引导种群。重复此过程，直到算法停止。 在每次迭代中，根据该算法的规则更新群体中每个成员的位置，并用目标函数评估新位置，这个过程会使解决方案随着每次迭代而优化。初始群体中每个成员的位置由式(1)在搜索空间中随机生成。

其中，xi 是猎人或猎物的位置，lb是问题变量的最小值(下界)，ub是问题变量的最大值(上界)，d是问题变量的数量(维度)。式(2)定义了搜索空间的下界和上界。需要注意的是，一个问题的所有变量的上下限可能相同或不同。 

生成初始总体并确定每个代理的位置后，使用目标函数Oi=f(→x) 计算每个解的适应度值。F(x)可以是最大值(效率、性能等)或最小值(成本、时间等)。搜索机制通常包括两个步骤：探索和开发。探索是指算法倾向于高度随机的行为，因此解决方案会发生显著变化。解决方案的重大变化促使猎人进一步探索搜索空间，并发现其有希望的领域。在发现有希望的区域后，必须减少随机行为，以便算法能够在有希望的区域周围搜索，这就是开发。

对于猎人的搜索机制，式(3)给出了其数学模型：

其中，x(t)是当前猎人位置，x(t+1)是猎人的下一次迭代位置，Ppos 是猎物的位置，μ是所有位置的平均值，Z是由式(4)计算的自适应参数： 

其中，→R1 和→R3 是[0,1]内的随机向量，P是→R1 的索引值，是 [0,1]内的随机数，IDX是满足条件(P==0)的向量的索引值，C是探索和开发之间的平衡参数，其值在迭代过程中从1减小到0.02，计算如下： 

 其中，it是当前迭代次数，MaxIt是最大迭代次数。计算猎物的位置Ppos ，以便首先根据式(6)计算所有位置的平均值(μ)，然后计算每个搜索代理与该平均位置的距离。

 根据式(7)计算欧几里得距离：

根据式(8)，距离位置平均值最大的搜索代理被视为猎物Ppos ： 

如果每次迭代都考虑到搜索代理与平均位置(μ)之间的最大距离，则该算法将具有延迟收敛性。根据狩猎场景，当猎人捕获猎物时，猎物会死亡，而下一次，猎人会移动到新的猎物位置。为了解决这个问题，考虑一种递减机制，如式(9)所示：

其中N是搜索代理的数量。

改变式(8)，将猎物的位置计算为式(10)：

在算法开始时， kbest的值等于N。因此，最后一个距离搜索代理的平均位置(μ)最远的搜索代理被选择为猎物，并被猎人捕获。

假设最佳安全位置是最佳全局位置，因为这将使猎物有更好的生存机会，猎人可能会选择另一个猎物。式(11)用于更新猎物位置：

其中，x(t)是猎物的当前位置；x(t+1)是猎物的下一次迭代位置；Tpos 是全局最优位置；Z是由式(4)计算的自适应参数；是范围[−1,1]内的随机数；C是探索和开发之间的平衡参数，其值在算法的迭代过程中减小，并由式(5)计算；cos函数及其输入参数允许下一个猎物位置在不同半径和角度的全局最优位置，并提高开发阶段的性能。

为了选择猎人和猎物，结合式(3)和(11)提出了式(12)：

其中，R5 是[0,1]范围内的随机数，β是一个调节参数，在本算法中的值设置为0.1。如果R5 值小于β，搜索代理将被视为猎人，搜索代理的下一个位置将用式(12a)更新；如果R5 值大于β，搜索代理将被视为猎物，搜索代理的下一个位置将用式(12b)更新。 

6.2 HPO猎人猎物优化算法寻找最优参数值

关键代码：

误差曲线图：

 最优参数：

6.3 最优参数值构建模型

7.模型评估

7.1 评估指标及结果

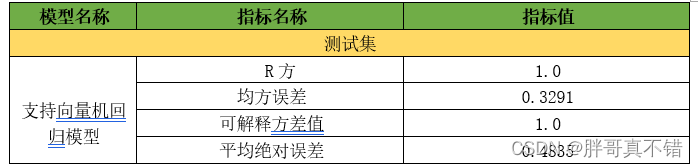
评估指标主要包括可解释方差值、平均绝对误差、均方误差、R方值等等。

从上表可以看出，R方1.0，为模型效果较好。

关键代码如下：

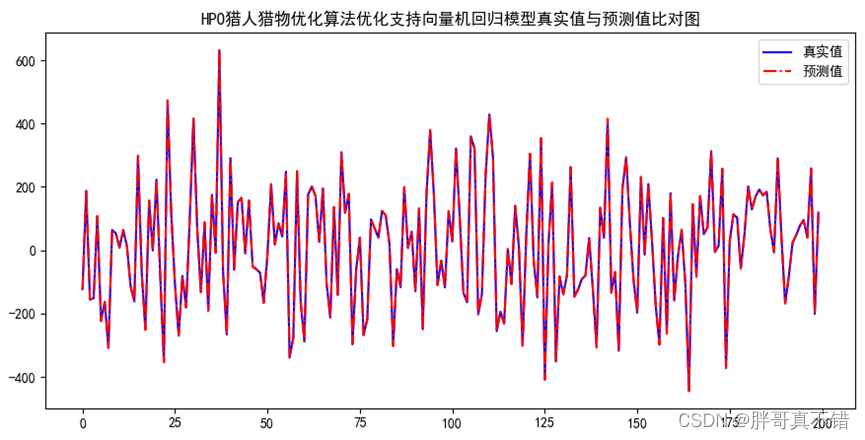
7.2 真实值与预测值对比图

从上图可以看出真实值和预测值波动基本一致，模型拟合效果良好。  

8.结论与展望

综上所述，本文采用了HPO猎人猎物优化算法寻找支持向量机SVR算法的最优参数值来构建回归模型，最终证明了我们提出的模型效果良好。此模型可用于日常产品的预测。

本次机器学习项目实战所需的资料，项目资源如下：

项目说明：
链接：https://pan.baidu.com/s/1c6mQ_1YaDINFEttQymp2UQ 
提取码：thgk