文章目录
- 5.1 树的基本概念
- 5.1.1 树的定义
- 5.1.2 森林的定义
- 5.1.3 树的术语
- 5.1.4 树的表示
- 5.2 二叉树
5.1 树的基本概念
5.1.1 树的定义
- 一棵树是结点的有限集合T:
- 若T非空,则:
- 有一个特别标出的结点,称作该树的根,记为root(T);
- 其余结点分成若干个不相交的非空集合T1, T2, …, Tm (m>0),其中T1, T2, …, Tm又都是树,称作root(T)的子树。
- T 空时为空树,记作root(T)=NULL。
- 若T非空,则:
5.1.2 森林的定义
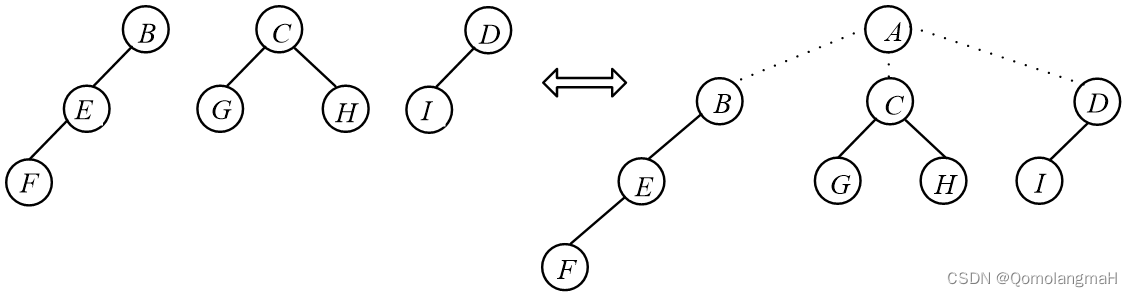
一个森林是0棵或多棵不相交(非空)树的集合,通常是一个有序的集合。换句话说,森林由多个树组成,这些树之间没有交集,且可以按照一定的次序排列。在森林中,每棵树都是独立的,具有根节点和子树,树与树之间没有直接的连接关系。
森林是树的扩展概念,它是由多个树组成的集合。在计算机科学中,森林也被广泛应用于数据结构和算法设计中,特别是在图论和网络分析等领域。
5.1.3 树的术语
- 父亲(parent)、儿子(child)、兄弟(sibling)、后裔(descendant)、祖先(ancestor)
- 度(degree)、叶子节点(leaf node)、分支节点(internal node)
- 结点的层数
- 路径、路径长度、结点的深度、树的深度
参照前文:【数据结构】树与二叉树(一):树(森林)的基本概念:父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度
5.1.4 树的表示
- 【数据结构】树与二叉树(二):树的表示C语言:树形表示法、嵌套集合表示法、嵌套括号表示法 、凹入表示法
5.2 二叉树
5.2.1 二叉树
1. 定义
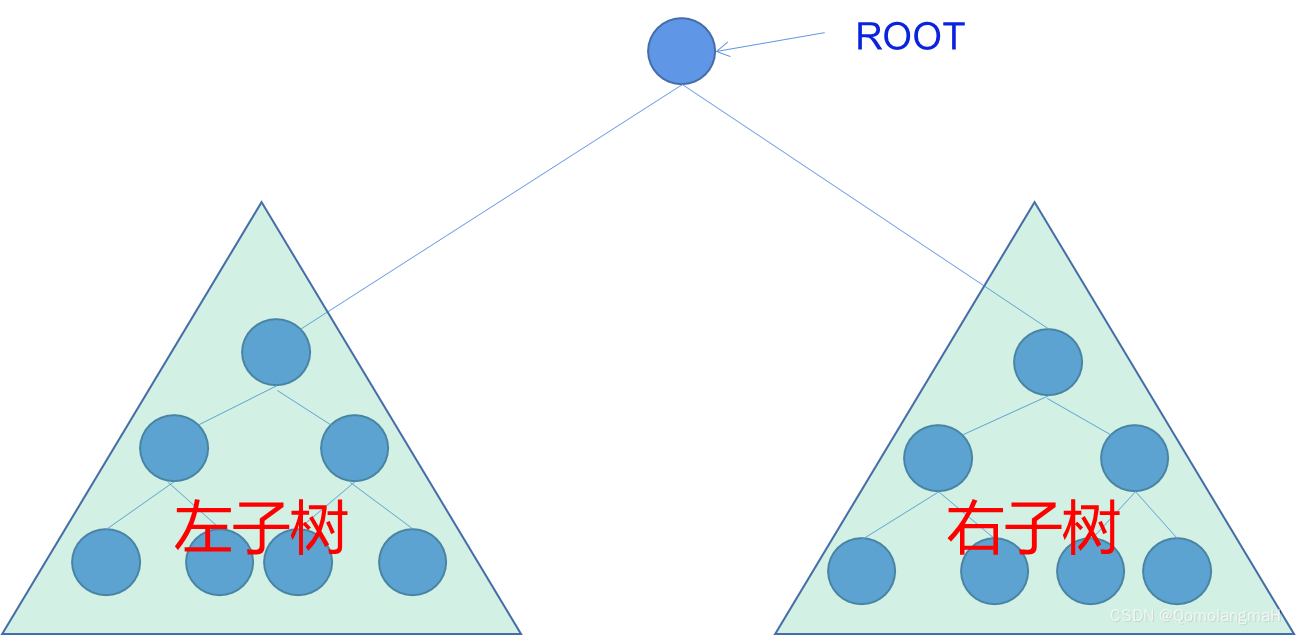
二叉树是一种常见的树状数据结构,它由结点的有限集合组成。一个二叉树要么是空集,被称为空二叉树,要么由一个根结点和两棵不相交的子树组成,分别称为左子树和右子树。每个结点最多有两个子结点,分别称为左子结点和右子结点。
2. 特点
二叉树的特点是每个结点最多有两个子结点,并且子结点的位置是有序的,即左子结点在前,右子结点在后。这种有序性使得二叉树在搜索、排序等算法中有广泛的应用。
-
在二叉树中,根结点是整个树的起始点,通过根结点可以访问到整个树的其他结点。每个结点都可以看作是一个独立的二叉树,它的左子树和右子树也是二叉树。
-
二叉树可以是空树,也可以是只有根结点的树,或者是由多个结点组成的树。每个结点可以包含一个数据元素,以及指向左子结点和右子结点的指针。
-
二叉树的形状可以各不相同,它可以是平衡的或者不平衡的,具体取决于结点的分布情况。在二叉树中,每个结点的左子树和右子树都是二叉树,因此可以通过递归的方式来处理二叉树的操作。
3. 性质
-
引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。
- 这个引理表明,二叉树的每一层上的结点数量是指数级增长的。
-
引理5.2:高度为k的二叉树中至多有 2 k + 1 − 1 2^{k+1}-1 2k+1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。
- 这个引理说明了二叉树的高度与结点数量之间的关系,高度越大,结点数量也越多。
-
引理5.3:设T是由n个结点构成的二叉树,其中叶结点个数为 n 0 n_0 n0,度数为2的结点个数为 n 2 n_2 n2,则有 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1。
- 这个引理描述了二叉树中叶结点和度数为2的结点之间的关系,即叶结点的数量比度数为2的结点数量多1。
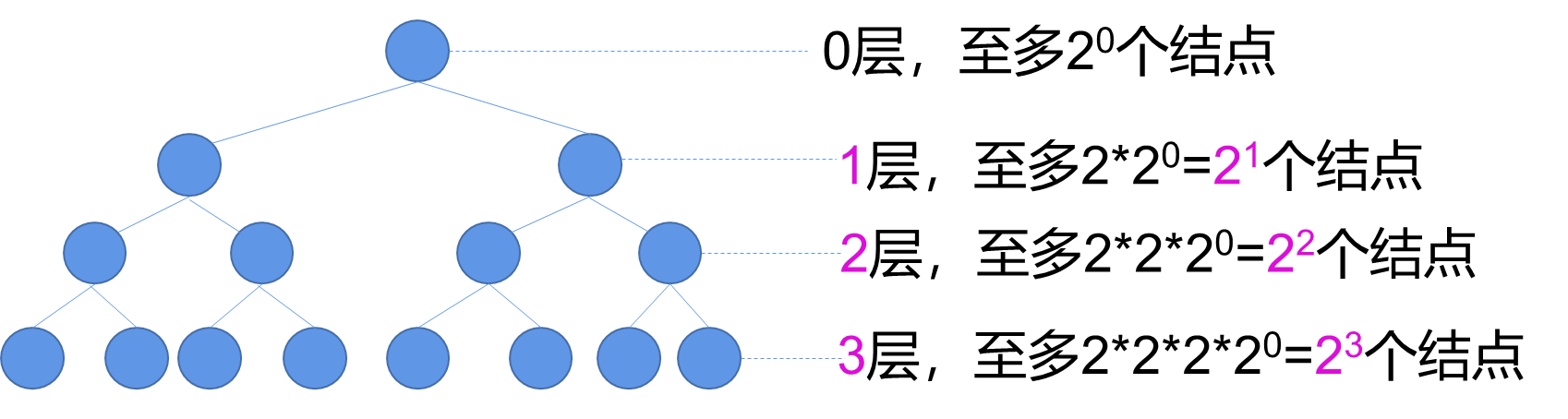
引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。
证明:使用数学归纳法。
基础步骤: 当 i = 0 i=0 i=0 时,仅有一个根结点,其层数为0。因此,第0层上至多有 2 0 = 1 2^0=1 20=1 个结点。因此,当 i = 0 i=0 i=0 时,引理成立。
归纳假设: 假设当 i = j i=j i=j ( j ≥ 0 ) (j\geq0) (j≥0) 时,二叉树中第 j j j 层上至多有 2 j 2^j 2j 个结点。
归纳步骤: 考虑第 j + 1 j+1 j+1 层上的结点个数。对于任意一个结点,其子结点个数最多为2。根据归纳假设,第 j j j 层上至多有 2 j 2^j 2j 个结点。因此,第 j + 1 j+1 j+1 层上的结点个数最多为 2 × 2 j = 2 j + 1 2\times2^j=2^{j+1} 2×2j=2j+1 个结点。
因此,根据数学归纳法,对于任意非负整数 i i i,二叉树中层数为 i i i 的结点至多有 2 i 2^i 2i 个。
证毕
引理5.2:高度为k的二叉树中至多有 2 k + 1 − 1 2^{k+1}-1 2k+1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。
对于高度为k的二叉树,我们可以计算每一层的最大结点数,并将它们相加来得到总结点数的上界。根据引理5.1,第
i
i
i层上至多有
2
i
2^i
2i个结点。那么,第
0
0
0层至第
k
k
k层的结点数上界可以表示为:
2
0
+
2
1
+
2
2
+
.
.
.
+
2
k
2^0 + 2^1 + 2^2 + ... + 2^k
20+21+22+...+2k
这是一个等比数列的和,可以使用等比数列求和公式进行计算。等比数列的求和公式为:
S = a ∗ ( r n − 1 ) / ( r − 1 ) S = a * (r^n - 1) / (r - 1) S=a∗(rn−1)/(r−1)
其中,S表示数列的和,a是首项,r是公比,n是项数。
在我们的情况下,首项a=1,公比r=2,项数n=k+1。将这些值代入公式中,我们可以得到:
2 0 + 2 1 + 2 2 + . . . + 2 k = 1 ∗ ( 2 k + 1 − 1 ) / ( 2 − 1 ) = 2 k + 1 − 1 2^0 + 2^1 + 2^2 + ... + 2^k =1 * (2^{k+1} - 1) / (2 - 1) = 2^{k+1} - 1 20+21+22+...+2k=1∗(2k+1−1)/(2−1)=2k+1−1
因此,高度为k的二叉树中至多有2^(k+1) - 1个结点。
证毕
- 问题1:高度为k (k≥1)的二叉树中至少有多少个结点?k+1
- 问题2:含有k (k≥1)个结点的二叉树高度至多为多少? k-1
引理5.3:设T是由n个结点构成的二叉树,其中叶结点个数为 n 0 n_0 n0,度数为2的结点个数为 n 2 n_2 n2,则有 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1。
设T是由 n n n个结点构成的二叉树,其中叶结点个数为 n 0 n_{0} n0,次数为2的结点个数为 n 2 n_{2} n2。
根据引理5.3的前提条件,我们有以下等式:
n = n 0 + n 1 + n 2 ( 5 − 1 ) n = n_{0} + n_{1} + n_{2} (5-1) n=n0+n1+n2 (5−1)
其中, n 1 n_{1} n1是T中次数为1的结点个数。
另一方面,设二叉树T的边的个数为 E E E。除了根结点外,每个结点和其父结点之间都有且仅有一条边,即一个结点对应一条边。因此,结点的个数 n n n比边的个数 E E E多1(根结点不对应边),即:
n = E + 1 ( 5 − 2 ) n = E + 1 (5-2) n=E+1 (5−2)
另外,从另一个角度来看,次数为1的结点对应一条边,次数为2的结点对应两条边。因此,边的个数 E E E可以表示为:
E = n 1 + 2 n 2 ( 5 − 3 ) E = n_{1} + 2n_{2} (5-3) E=n1+2n2 (5−3)
我们将(5-1)、(5-2)和(5-3)联立起来,通过求解这个方程组,我们可以得到 n 0 = n 2 + 1 n_{0} = n_{2} + 1 n0=n2+1,即二叉树T中的叶结点个数 n 0 n_{0} n0为次数为2的结点个数 n 2 n_{2} n2加1。
证毕


![壹[1],QT自定义控件创建(QtDesigner)](https://img-blog.csdnimg.cn/6093623977844fb4996b7a5698ce9914.png)